Calculus Final Exam - Limits Algebraically and Continuity

0.0(0)
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/11

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

12 Terms

1
New cards

If g is the function defined by g(x) = (cos x - sin x) / (1-2sin2x) , what is lim x → pi/4 g(x)?

1/sqrt (2)

2
New cards

Which of the following functions is not continuous on the interval −∞<x<∞ ?

A) f(x) = 4(x)2-2x + 1

B) g(x) = 1/ (x3 + 3(x)2 - 2x - 5)

C) h(x) = cos(pi x)

D) k(x) = 1 / ex

B) g(x) = 1/ (x3 + 3(x)2 - 2x - 5)

3
New cards

If f is the function defined by f(x)= (x2−4) / (x2+ x−6), then lim x→2 f(x) is

4/5

4
New cards
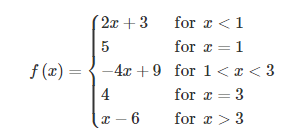
<p><span>Let f be the piecewise function defined above. Which of the following statements is false?</span></p><p><span>A) f is continuous at x =1 </span></p><p><span>B) f is continuous at x = 2</span></p><p><span>C) f is continuous at x = 3</span></p><p><span>D) f is continuous at x = 4</span></p>

Let f be the piecewise function defined above. Which of the following statements is false?

A) f is continuous at x =1

B) f is continuous at x = 2

C) f is continuous at x = 3

D) f is continuous at x = 4

C) f is continuous at x = 3

5
New cards


lim x→3 (x−3) / x3−9x) is

1/18

6
New cards
<p><span>Let g be a function that is increasing for x&lt;1 and increasing for x&gt;1. If lim⁢ x→1 g(x)=5, which of the following could represent the function g ?</span></p>

Let g be a function that is increasing for x<1 and increasing for x>1. If lim⁢ x→1 g(x)=5, which of the following could represent the function g ?

I and III only

7
New cards

If f is the function defined by f(x)= (x2−1) / √(x)−1, then lim x→1 f(x) is

4

8
New cards
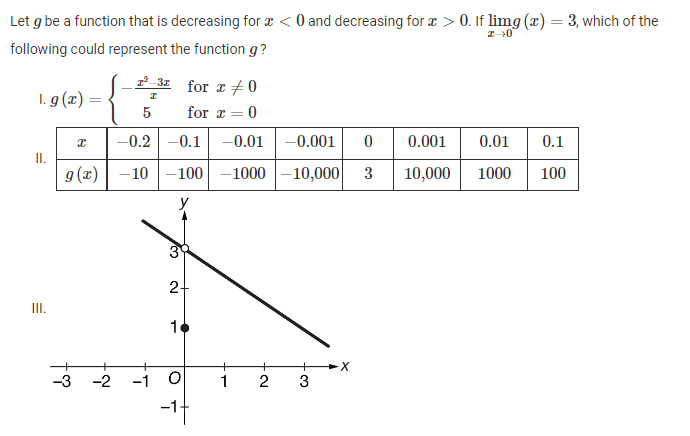
term image

Step 3

9
New cards
term image

I and III only

10
New cards
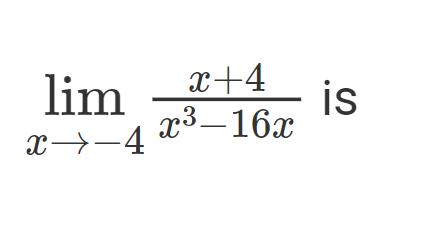
term image

1/32

11
New cards
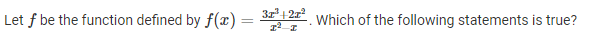
<p>A) f has a discontinuity due to a vertical asymptote at x = 0 and x = 1</p><p>B) f has a removable discontinuity at x = 0 and a jump discontinuity at x = 1</p><p>C) f has a removable discontinuity at x = 0 and a discontinuity due to a vertical asymptote at x = 1</p><p>D) f is continuous at x = 0, and f has a discontinuity due to a vertical asymptote at x = 1</p>

A) f has a discontinuity due to a vertical asymptote at x = 0 and x = 1

B) f has a removable discontinuity at x = 0 and a jump discontinuity at x = 1

C) f has a removable discontinuity at x = 0 and a discontinuity due to a vertical asymptote at x = 1

D) f is continuous at x = 0, and f has a discontinuity due to a vertical asymptote at x = 1

C) f has a removable discontinuity at x = 0 and a discontinuity due to a vertical asymptote at x = 1

12
New cards

The figure presents the graph of f in the x y coordinate plane, with the origin labeled O. The numbers negative 1 through 5, in increments of 1, are indicated on the x axis. The numbers 1 and 2 are indicated on the y axis. The graph consists of three line segments. Three open circles and four closed circles are included in the graph. The first line segment begins at a closed circle on the x axis at negative 1, and moves upward and to the right, passing through an open circle on the y axis at 1. It continues upward and to the right, until it ends at another open circle at the point with coordinates 1 comma 2. The second line segment begins at a closed circle on the x axis at 1, and moves upward and to the right, passing through an open circle at the point with coordinates 2 comma 1. It continues upward and to the right, until it ends at a closed circle at the point with coordinates 3 comma 2. The third line segment begins at the closed circle where the second line segment ends, moves downward and to the right, and ends at a closed circle on the x axis at 5.

The graph of the function f is shown above. What are all values of x for which f has a removable discontinuity?

0 and 2 only