Gr11 Math

Unit 1

Intro to Functions

Relation

A rule that associates an x-value with y-value(s)

Function

A special type of a relation in which there is only one value of dependent variable (y-value) for each value of the independent variable (x-values)

Meaning in a function when you plug in x you will only get one y value

Vertical Line Test

If any vertical line passes through more than one point on the graph, the relation is not a function

Domain

The set of possible values of the independent variable (x)

Ex. D={x∈R |0<x<5}

Range

The set of all possible values of the dependent variable (y)

Ex. R={y∈R |0<y<5}

Function Notation

f(x) = y

Sub in what is in the brackets to find f(x)

To find f(x) given another equation:

Asymptote

A line that the graph of a relation hets closer and closer to, but never meets

Axis of symmetry

When a vertical line can split a function evenly at a certain x coordinate

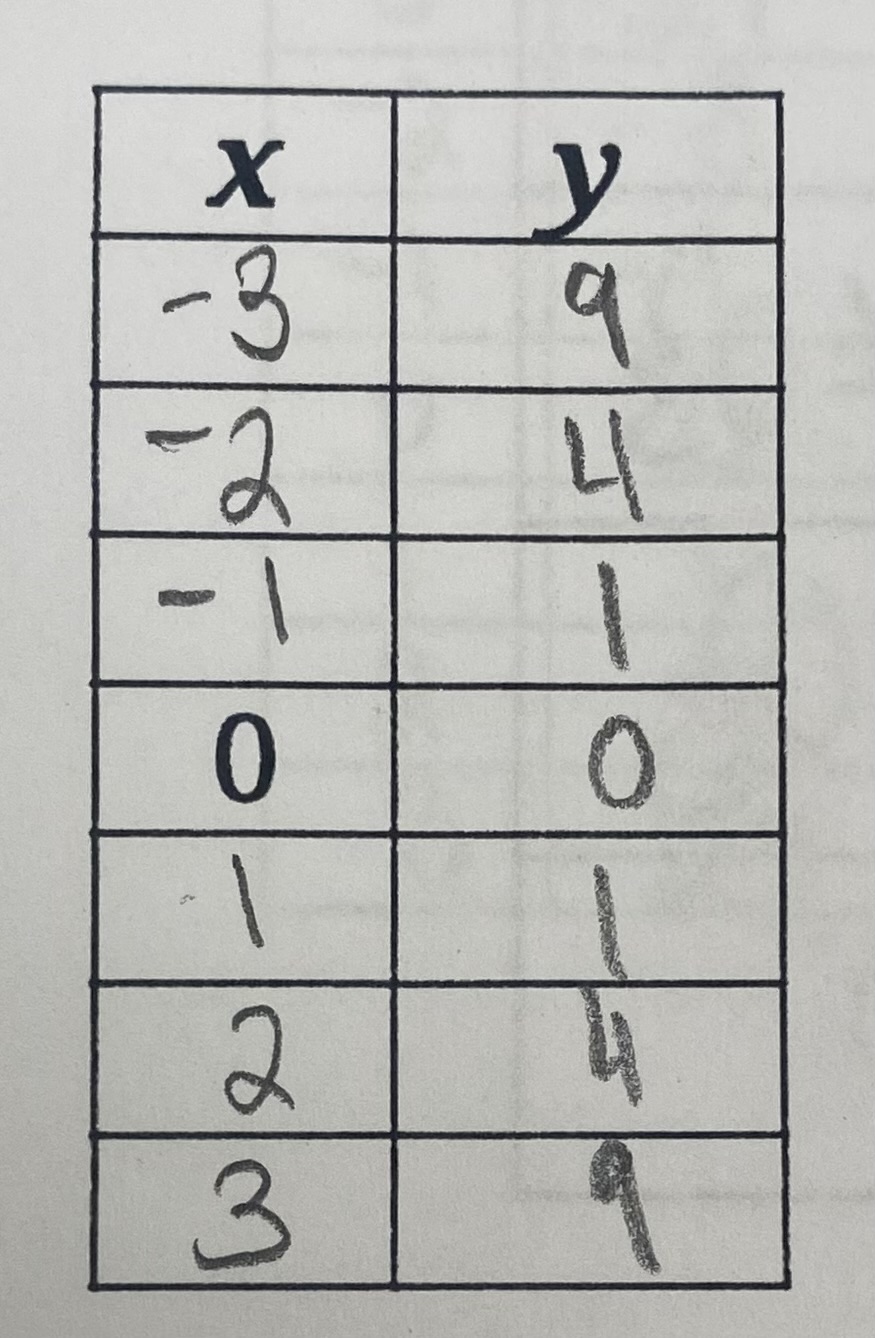
Quadratic Function (Parent Function)

f(x) = x²

AOS: x=0

D={x∈R}

R={y∈R|y=>0|}

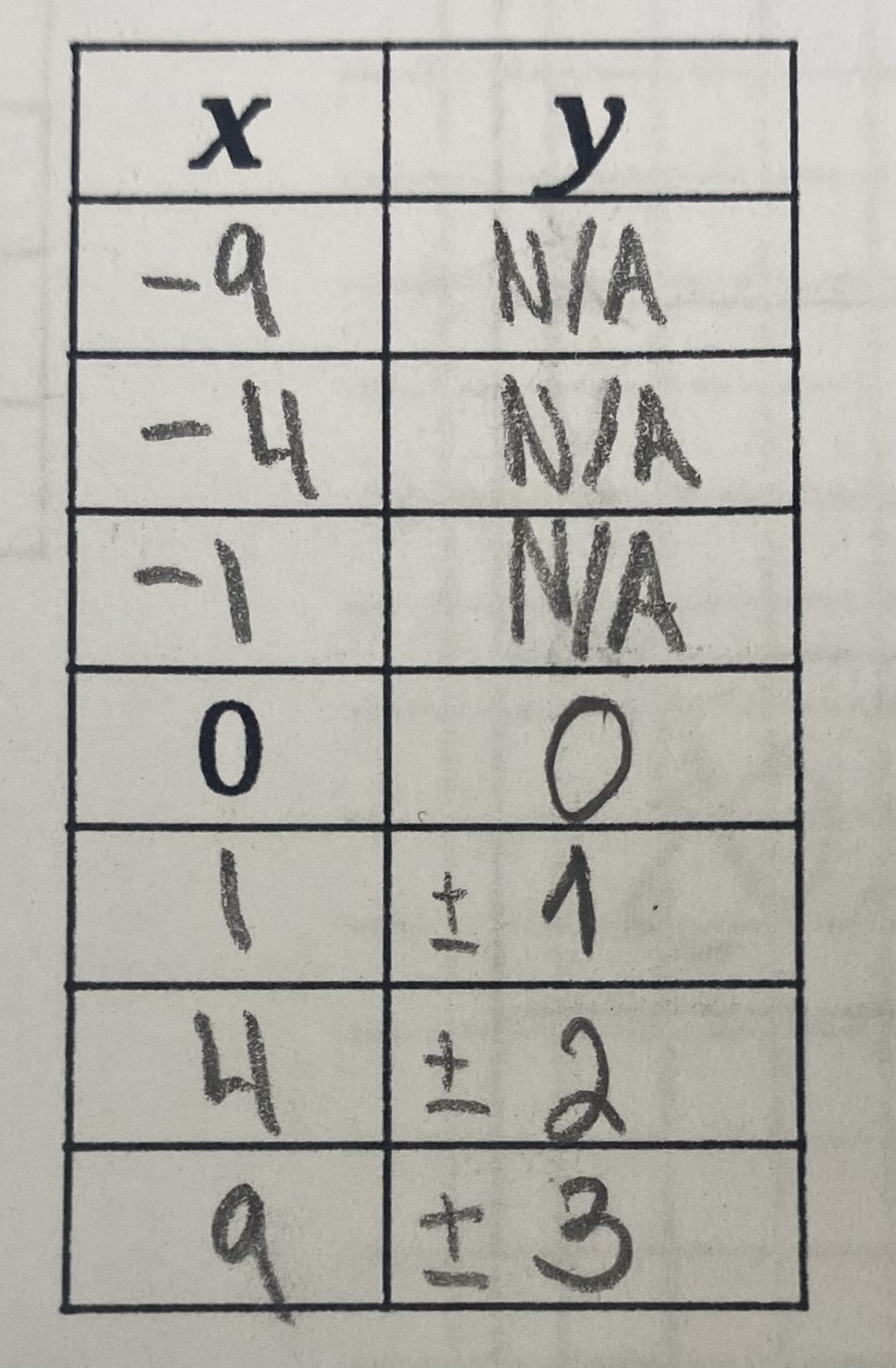
Square Root Function (Parent Function)

f(x) = √x

D={x∈R|x=>0|}

R={y∈R}

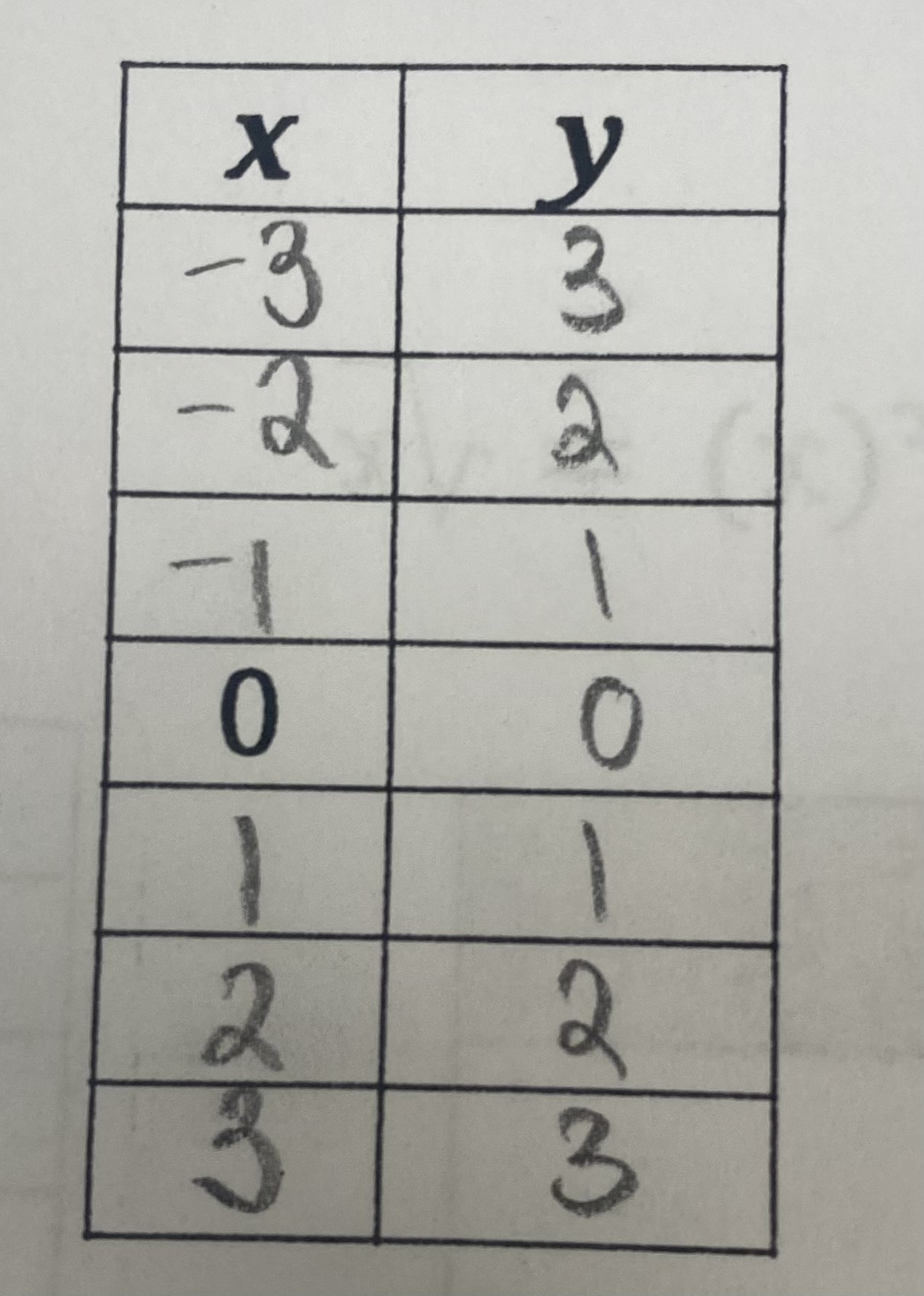
Reciprocal Function (Parent Function)

f(x) = 1/x

D={x∈R|x≠0}

R={y∈R|y≠0}

Asymptotes: y=0, x=0

Absolute Value Function (Parent Function)

f(x) = |x|

D={x∈R}

R={y∈R|y=>0|}

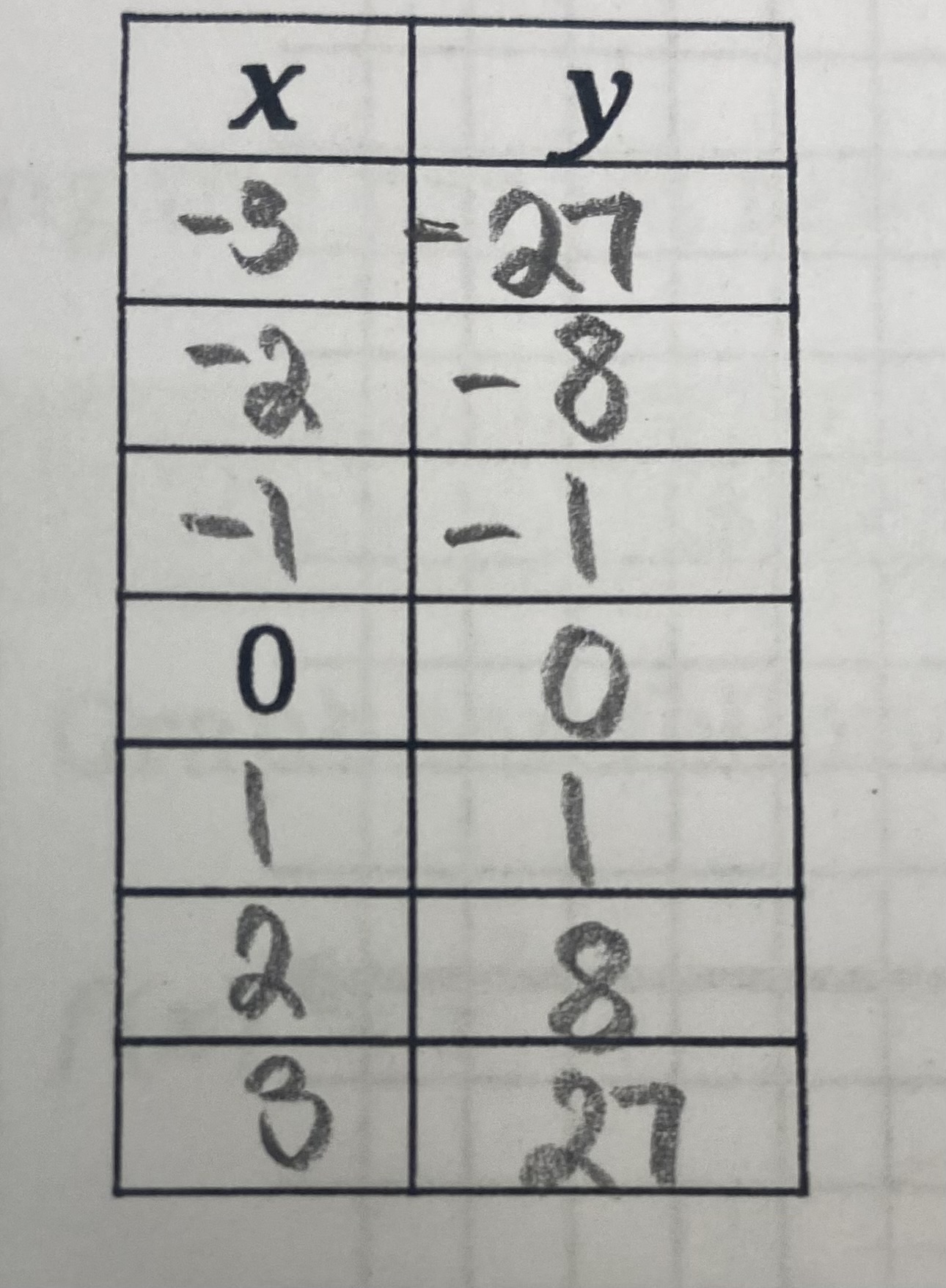
Cubic Function (Parent Function)

f(x) = x³

D={x∈R}

R={y∈R}

Vertical Transformation

c

y= x² + c

When c > 0, the parabola shifts vertically c units up

When c < 0, the parabola shifts vertically c units down

Horizontal Transformation

d

y= (x-d)²

When you use d switch its sign

When d > 0, the parabola shifts horizontally d units right

When d < 0, the parabola shifts horizontally d units left

Vertical Stretches/Compressions

a

y= a√x

When a is negative, the function is reflected in the x-axis

When |a|>1 the function is vertically stretched

When 0<|a|<1 the function is vertically compressed

Horizontal Stretches/Compressions

k

y= √kx

Put k over 1 when finding compression or stretch

When k is negative, the function is reflected in the y-axis

|k| > 1 the function is horizontally stretched bafo 1/k

0<|k|<1 the function is horizontally compressed bafo 1/k

Summary of transformations

Switch the k and d values for when you put them in this equation

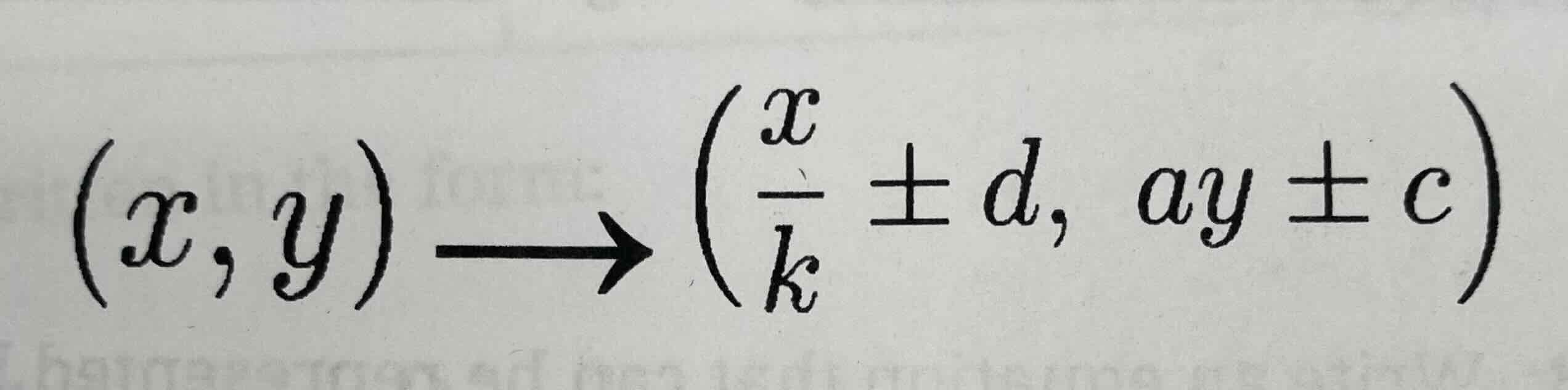
Equation of a transformed function

f(x) = a f (k(x-d)) + c

How to get inverse functions form the coordinates and algebraically

From coordinates just swap x and y

From expression switch places of x and y and solve for y

Remember that if you restrict ur inverse to make it a function, you have to restrict your original

Unit 2

Algebraic Expressions and Factoring

Polynomial

Expression with one or more terms

Factoring by grouping

1. Usually you will have 4 terms which you can split into 2 groups

2. Factor the GCF from those 2 terms

3. If you get a common term in the brackets then you did it right

4. Finally write two brackets one with the common term and the other with the 2 things you factored out

Factoring trinomials where the leading coefficient is 1

1. Factor out a GCF if there is one

2. Find two numbers that add up to get the b term and multiply to get the c term

3. Write the two numbers in brackets like this:

   (x + n1) (x + n2)

Factoring trinomials where the leading coefficient is not 1

1. Multiply the coefficient of the a term by the c term

2. Find 2 numbers that multiply to give you the new number and add to give you the b term

3. Replace the b term with those 2 numbers

4. Factor by grouping

Factoring a perfect square trinomial

Equation: A² + 2AB + B² = (A + B)²

1. Square root the a and c terms and then multiply them

2. Multiply that answer by 2 if you get the b term you can use the formula

3. Take the square root of the a and c terms then write it like this: (2x + 4)²

Factoring a difference of squares

Equation: A² - B² = (A + B) (A - B)

1. Make sure you can take the square root of both terms and that it is a minus they cant be added

2. Square root both terms and put them in 2 brackets one with a plus and the other with a minus

Note: Sometimes you can do this after taking out the GCF so after you take it out just leave it infront of the first bracket

Multiplying Rational Expressions

Steps:

1. Factor

2. Restrict

3. Multiply (use brackets)

4. Simplify (cancel)

Dividing Rational Expressions

Steps:

1. Factor

2. Restrict

3. Keep Change Flip

4. Restrict

5. Multiply

6. Simplify

Adding/Subtracting Rational Expressions

Steps:

1. Factor

2. Restrict

3. LCD

4. Expand (Numerator only)

5. Simplify (Factor and Cancel)

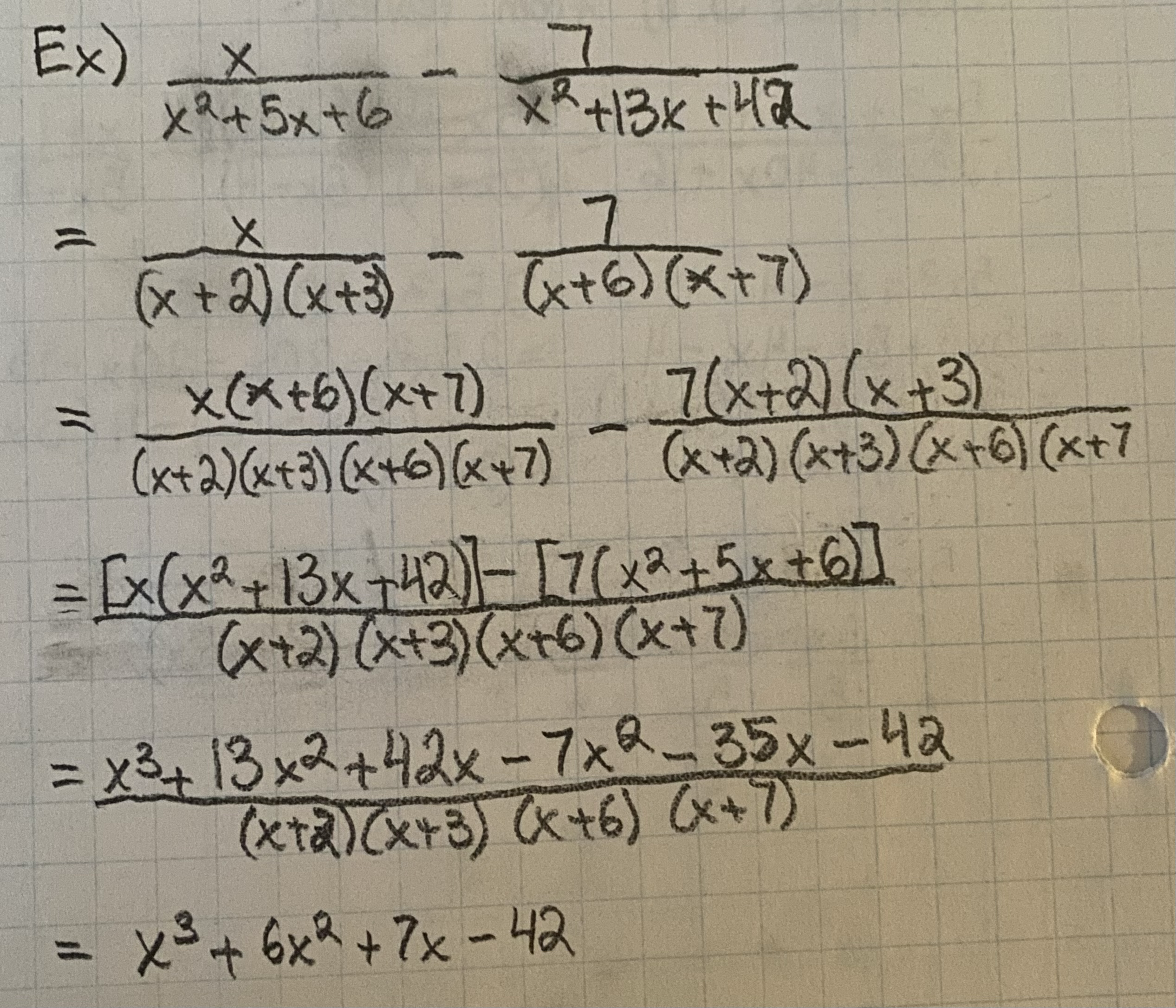
Unit 3

Quadratic Functions

Graphing a quadratic

Quadratic functions are a parabola

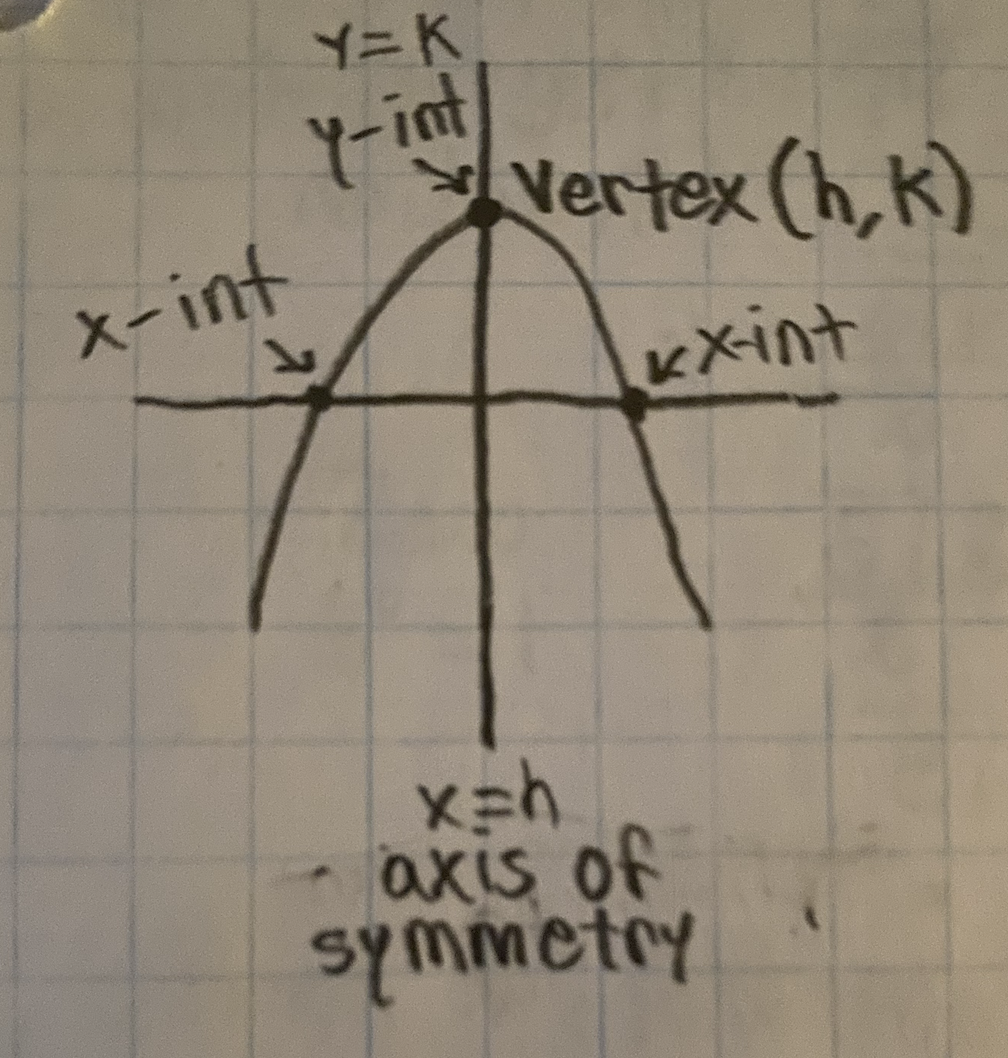
Three forms of Quadratic Equations

• Standard Form

  = ax² + bx + c

  a: Direction of Opening

  c: y- intercept

• Factored form

  = a(x-s)(x-t)

  s: x-int

  t: x-int

• Vertex Form

  = a(x-h)² + k

  h: x-value of vertex

  k: y-value of vertex

How to solve a quadratic equation

To solve a quadratic equation means to solve for x meaning you are looking for the x-intercepts or roots

The 3 ways of solving are:

1. Quadratic Formula

2. Factoring

3. Isolating for x (if its in vertex form)

How to find the vertex of a parabola

If the equation is in standard for you can find the x-value of the vertex using h = -b/2a

Then you can plug in h into the equation to find the y-value of the vertex

Parts of a Radical and Radical types

Index: The number that it is being rooted by usually a small number left of the radical symbol

Radicand: The expression under the radical sign

Entire Radical: √10 (has coefficient of 1)

Mixed Radical: 3√5 (has coefficient other than 1)

Laws of Radicals (Multiplication and Division)

Multiplication: First multiply Coefficients with Coefficients and Radicals with Radicals, then reduce if there is a radical that can be reduced

6√20 → 12√5

Division: Reduce by making sure there is no radical on the bottom, this can be done by reducing and multiplying both sides

Adding/Subtracting Radicals

Simplify radicals into mixed radicals and collect like terms

Rationalizing the Denominator

This means to make the denominator not have any radicals

Sometimes this can be done by multiplying by the conjugate

Conjugate: binomial with opposite sign in the between the 2 terms

Solving Linear-Quadratic Systems

Means to find the point(s) of intersection of a linear and quadratic equation

Steps:

1. Make equations equal to each other

2. Make equation equal to 0 to solve

3. Plug in solutions into original equations to find y-values

Unit 4

Exponential Functions

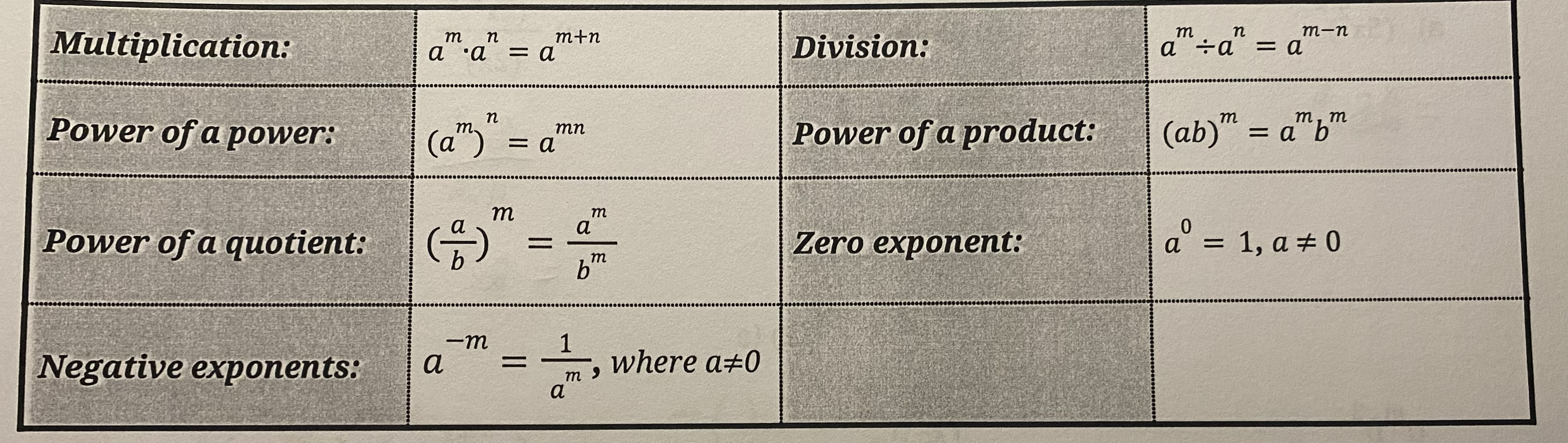
Exponent Laws (multiplication, division, quotient, power, product, zero, negative)

What is a rational exponent

Something to the power of a fraction

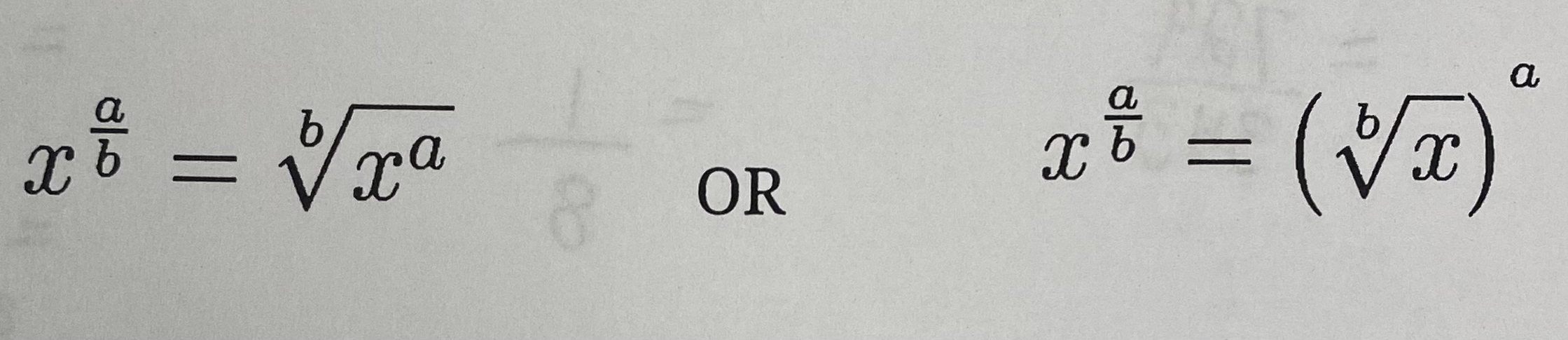
Equation of Exponential functions

f(x) = a(b)^x

Growth: b > 1

Decay: b < 1

*b is always positive

Properties of a Exponential function

Transforming an Exponential function

Increasing base exponential function that we use

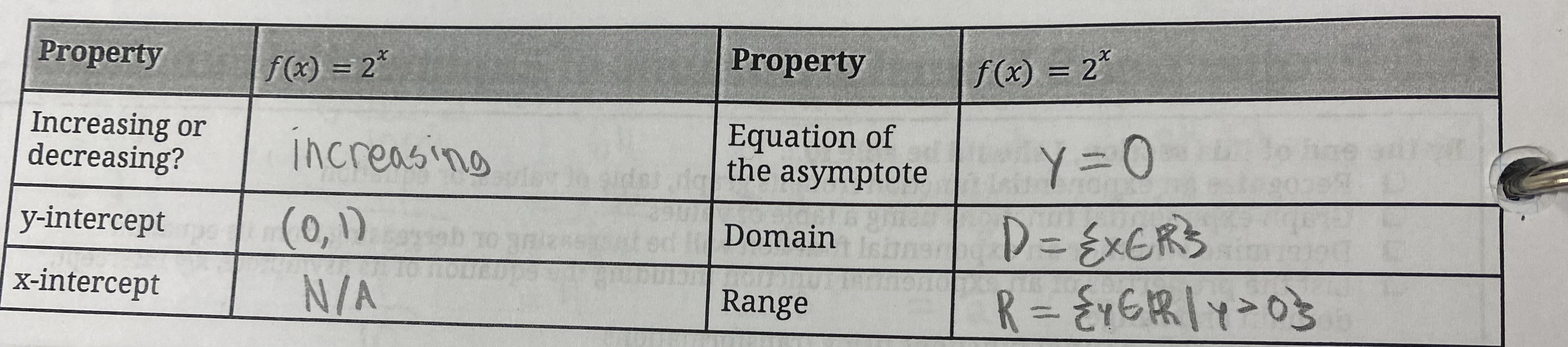
Decreasing base exponential function that we use

How to solve exponential equations

1. Rewrite both sides with the same base (by changing the larger numbers exponent)

2. Set the exponents equal to each other

3. Solve for the variable

Solving exponential equations using logs

Do the log of the number without the exponent divided by the log of the number with the exponent

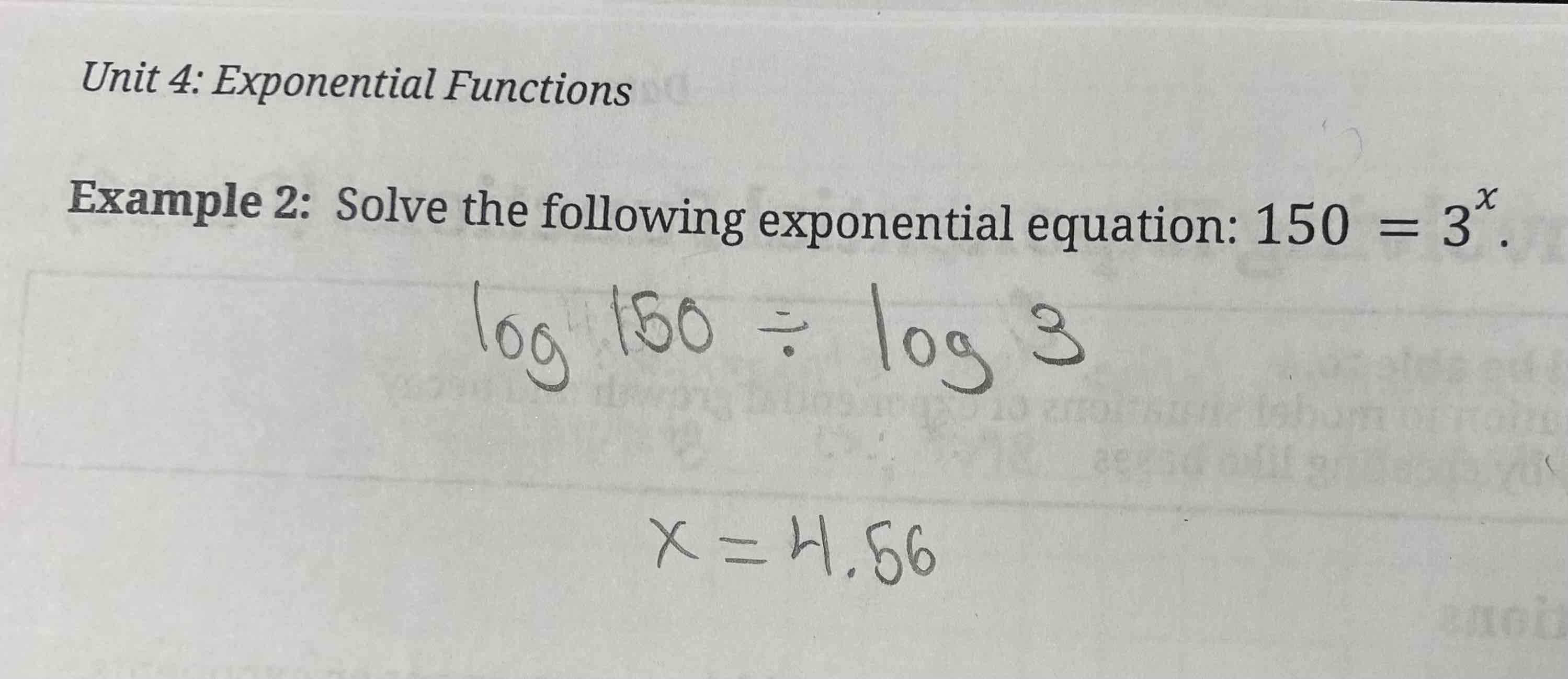
How to model with exponential equations

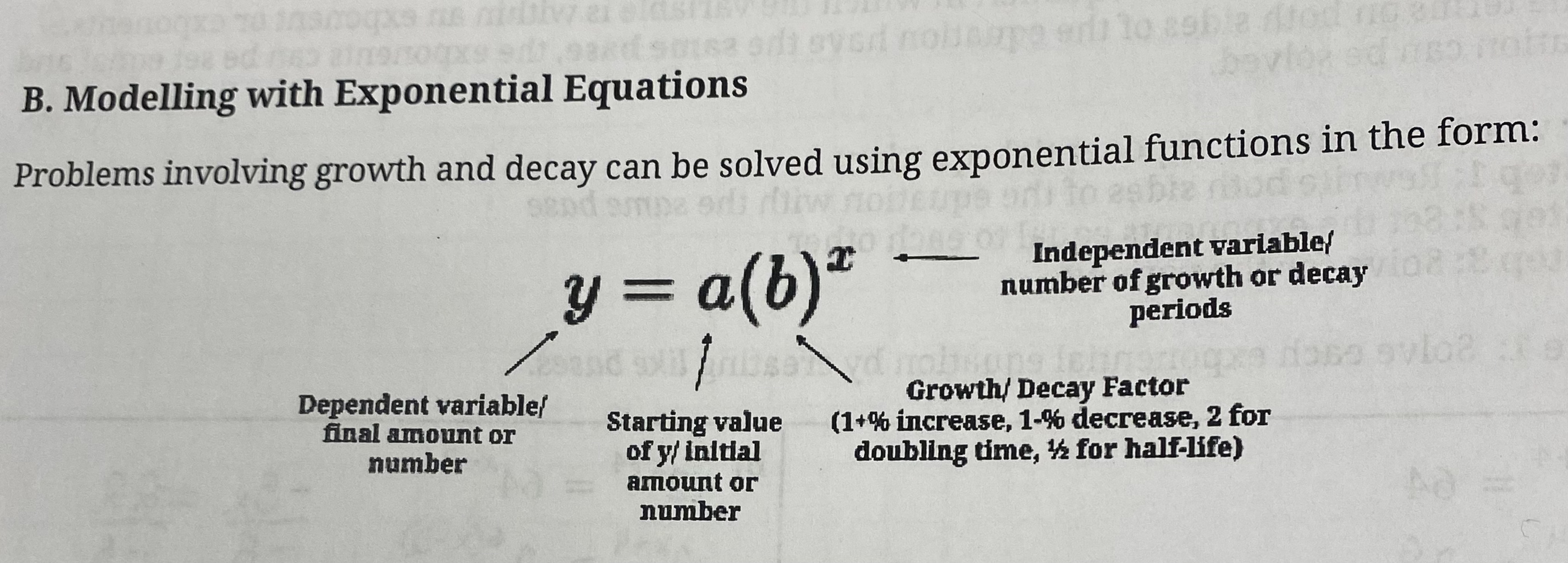
Unit 5

Trigonometry

Trigonometry of Acute Angles (review)

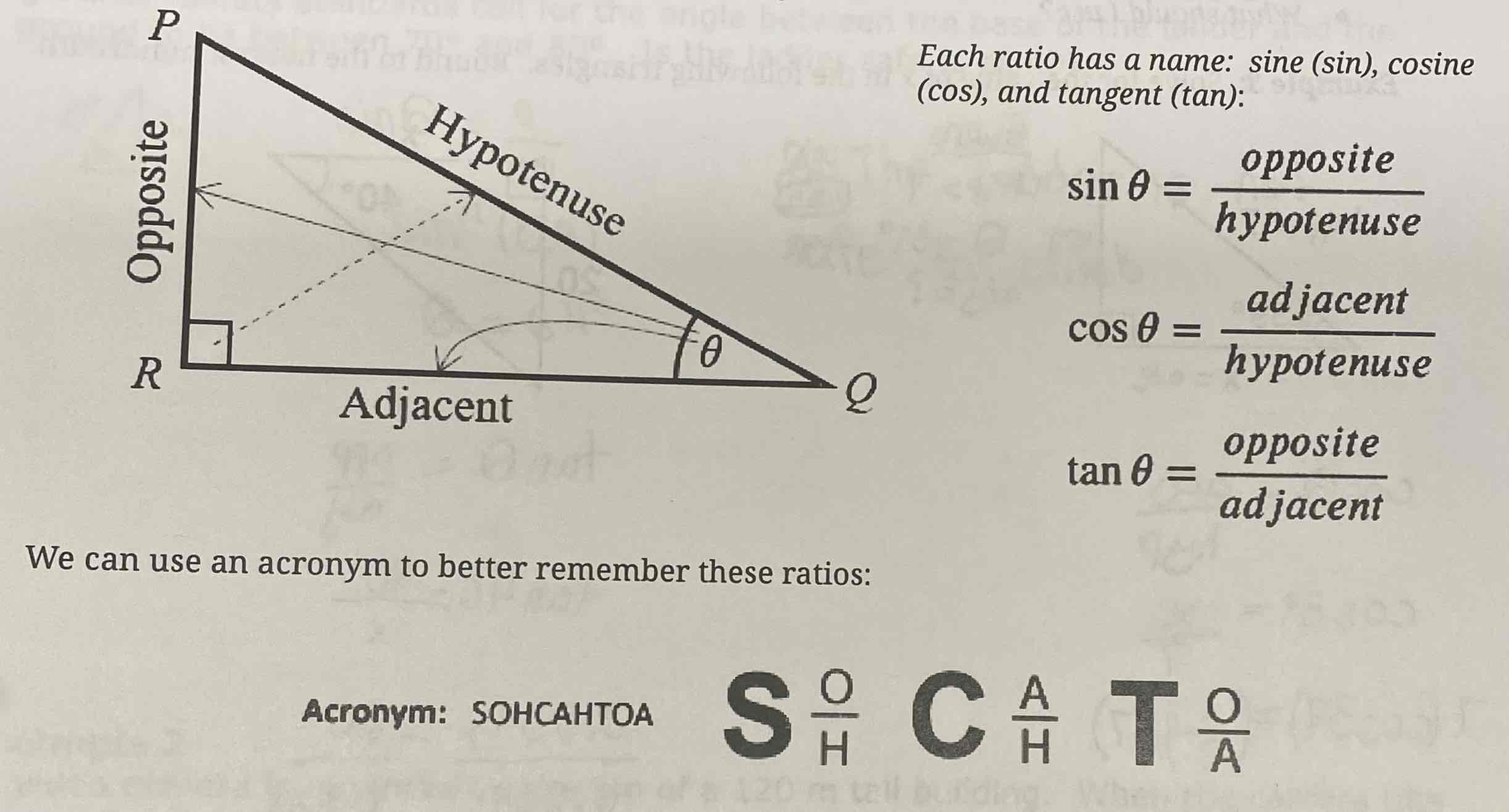
Angle of depression vs elevation

Depression is the line of sight when you are looking down

Elevation is the line of sight when you are looking up

Secondary Trigonometric Ratios

Angles in Standard Position (What is the initial arm, termial arm, principal angle, related acute angle, vertex, 4 quadrants)

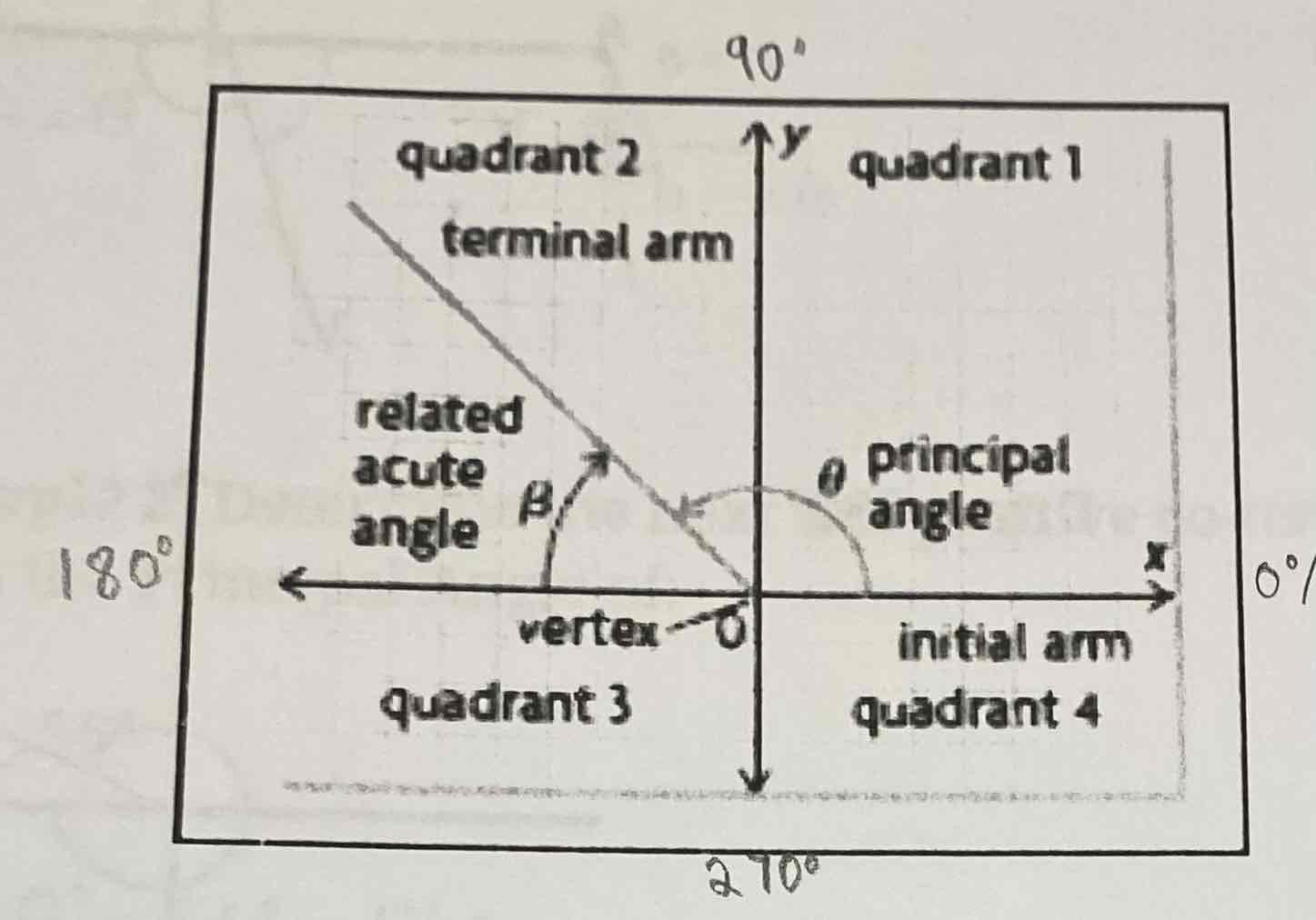
Positive vs Negative Angle

A positive angle goes up from the initial arm

A negative angle goes down from the initial arm

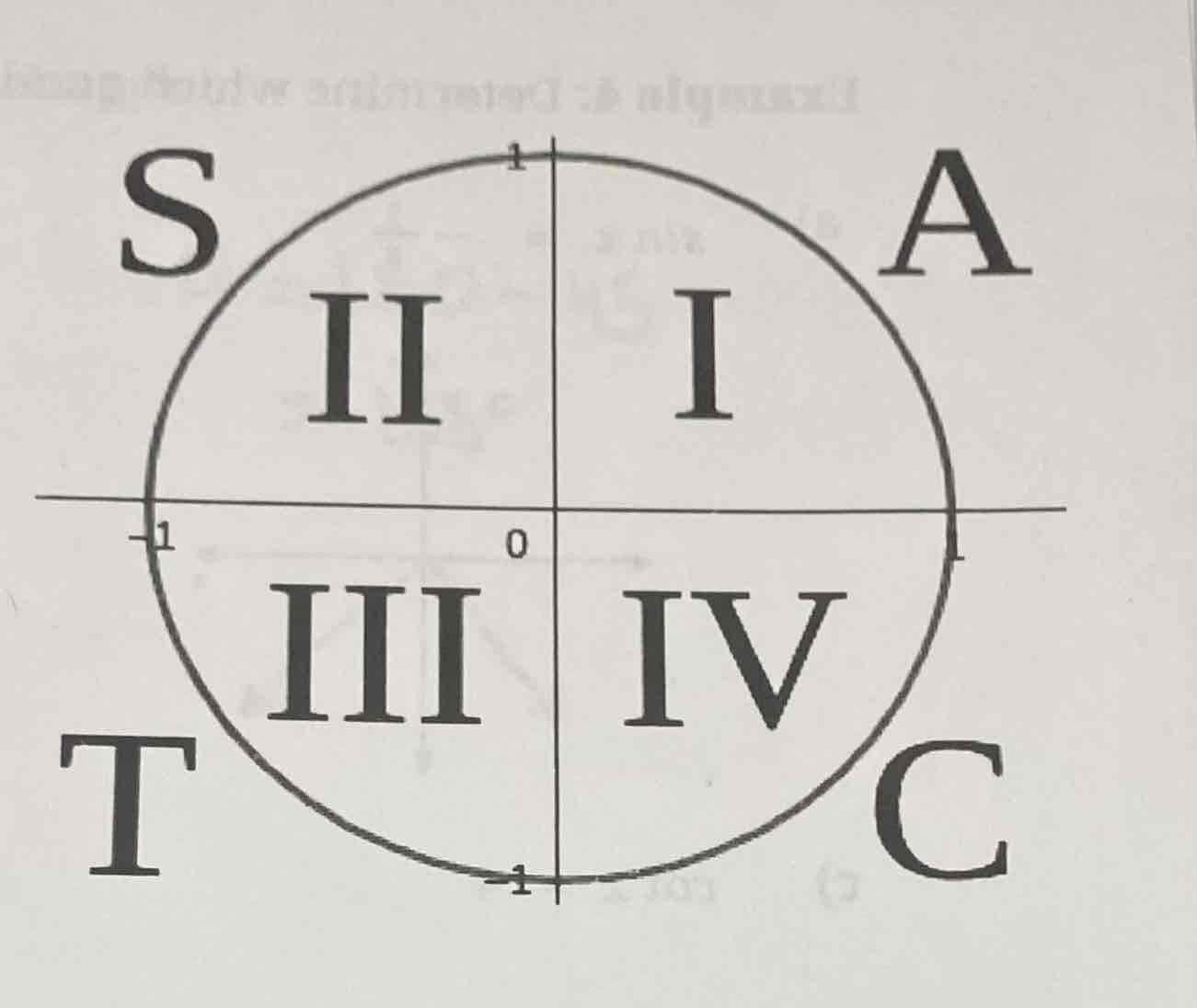
CAST rule

Way to remember which trig ratios are positive in each quadrant

COSINE-ALL-SINE-TANGENT

Sine Law

*Capital letters are angles lowercase are side lengths

You need an angle and its opposite side length to use sine law

If you are looking for an angle use the formula with angles on top

If you are looking for a side length use the formula with the side lengths on top

Cosine Law

*Capital letters are angles lowercase are side lengths

Use cosine law if you have 2 sides and an angle or 3 sides

Ambiguous Case

When using sine law you can get 2 different angles (θ and 180° - θ)
So when using sine law it can be used to find another angle on the same line

Trig Identities

Prove that the left side is equal to the right side

1. Change everything to sin0 and cos0

2. If there are fractions being added or subtracted find a common denominator and combine the fractions

3. Use difference of squares

4. Use the power rule

Unit 6 Sinusoidal Functions

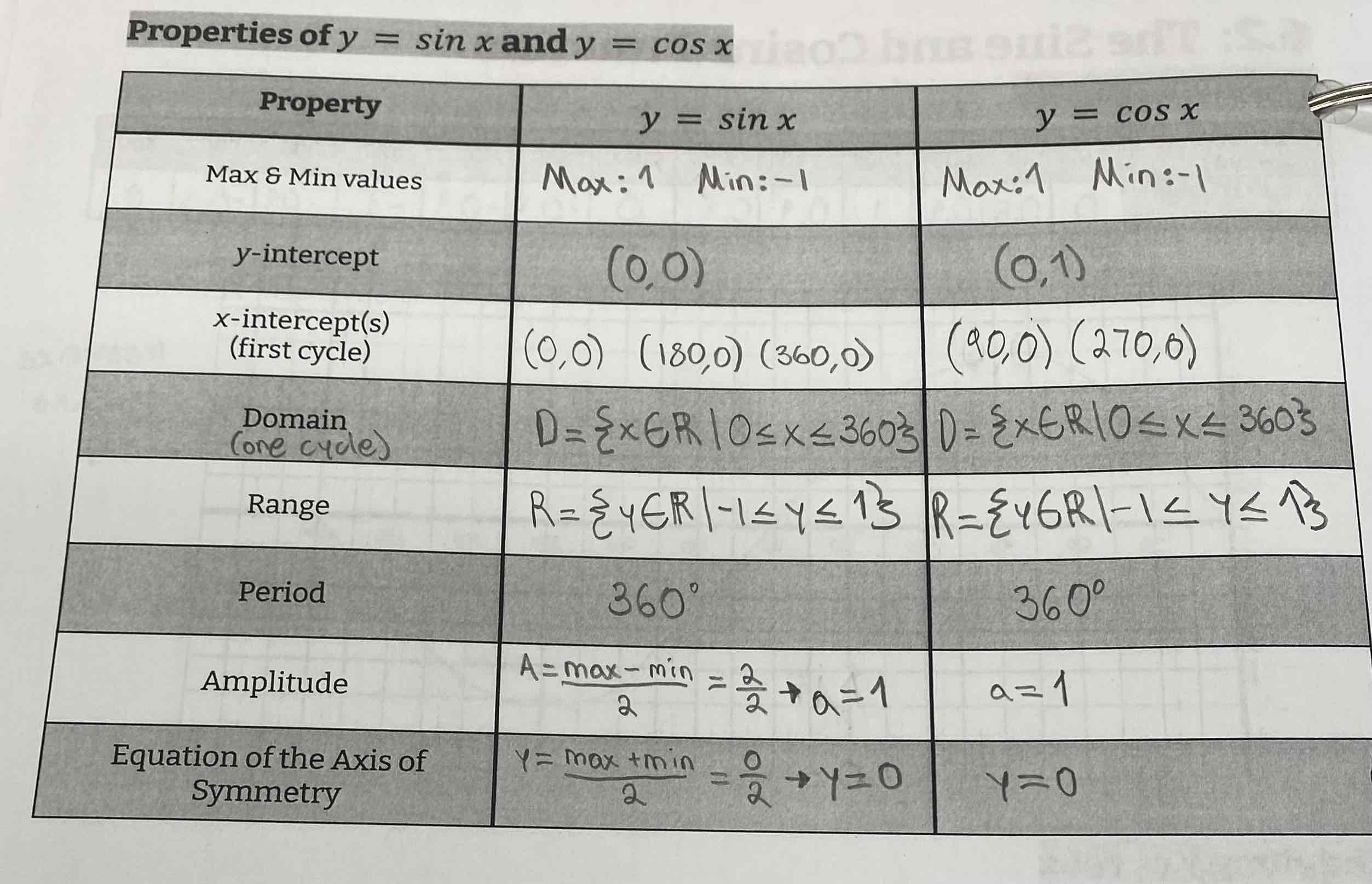
Period

The length of one cycle (A cycle is one complete pattern in the graph)

Equation of the axis of the curve

The horizontal line that cuts the graph in half.

*Remember to use y = when writing it cause its an equation

y = (max + min) / 2

Amplitude

The distance from the axis of the curve to the max or min of the graph

y = (max - min) / 2

Graphing Sine Function

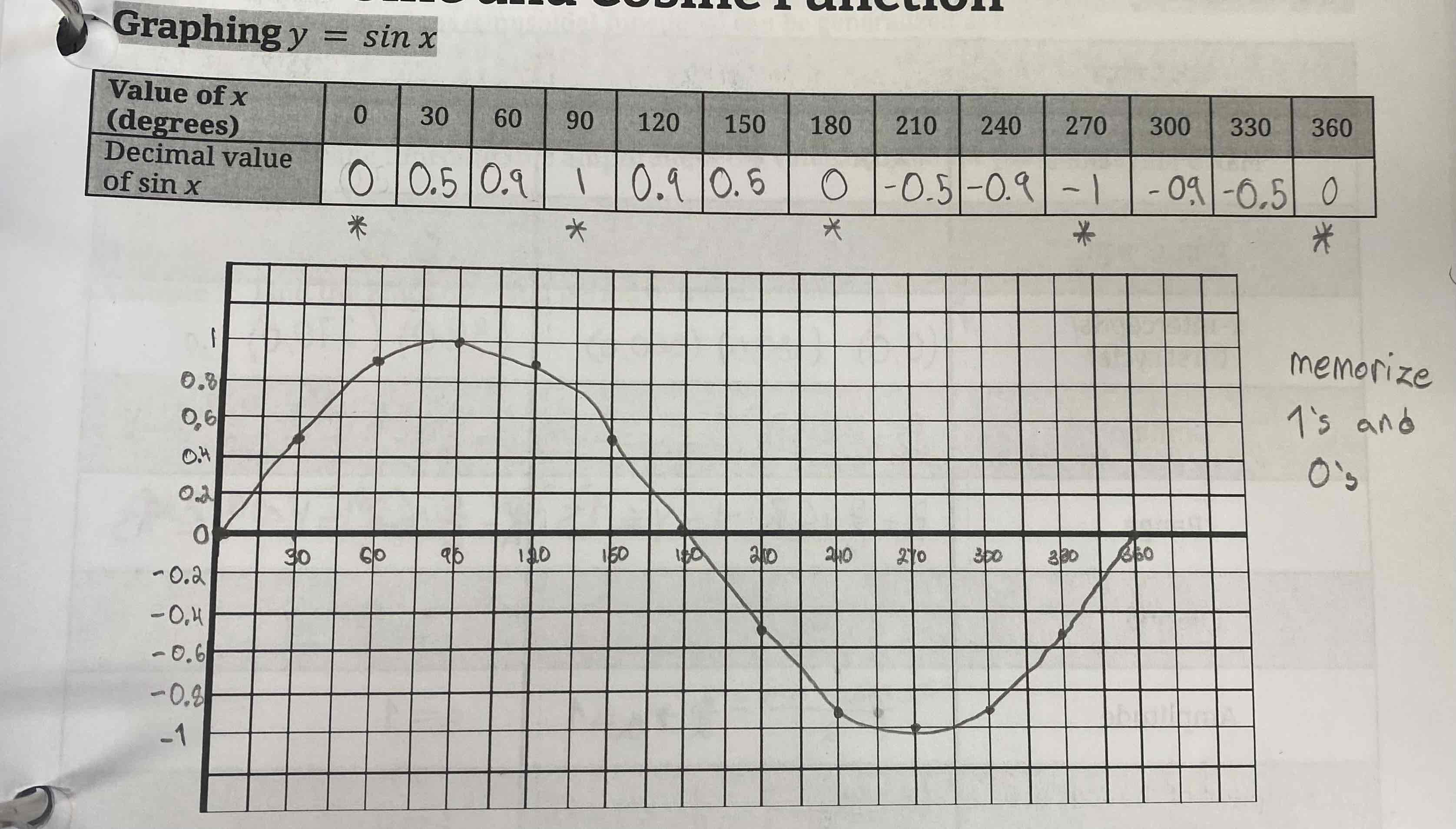
Graphing Cosine Function

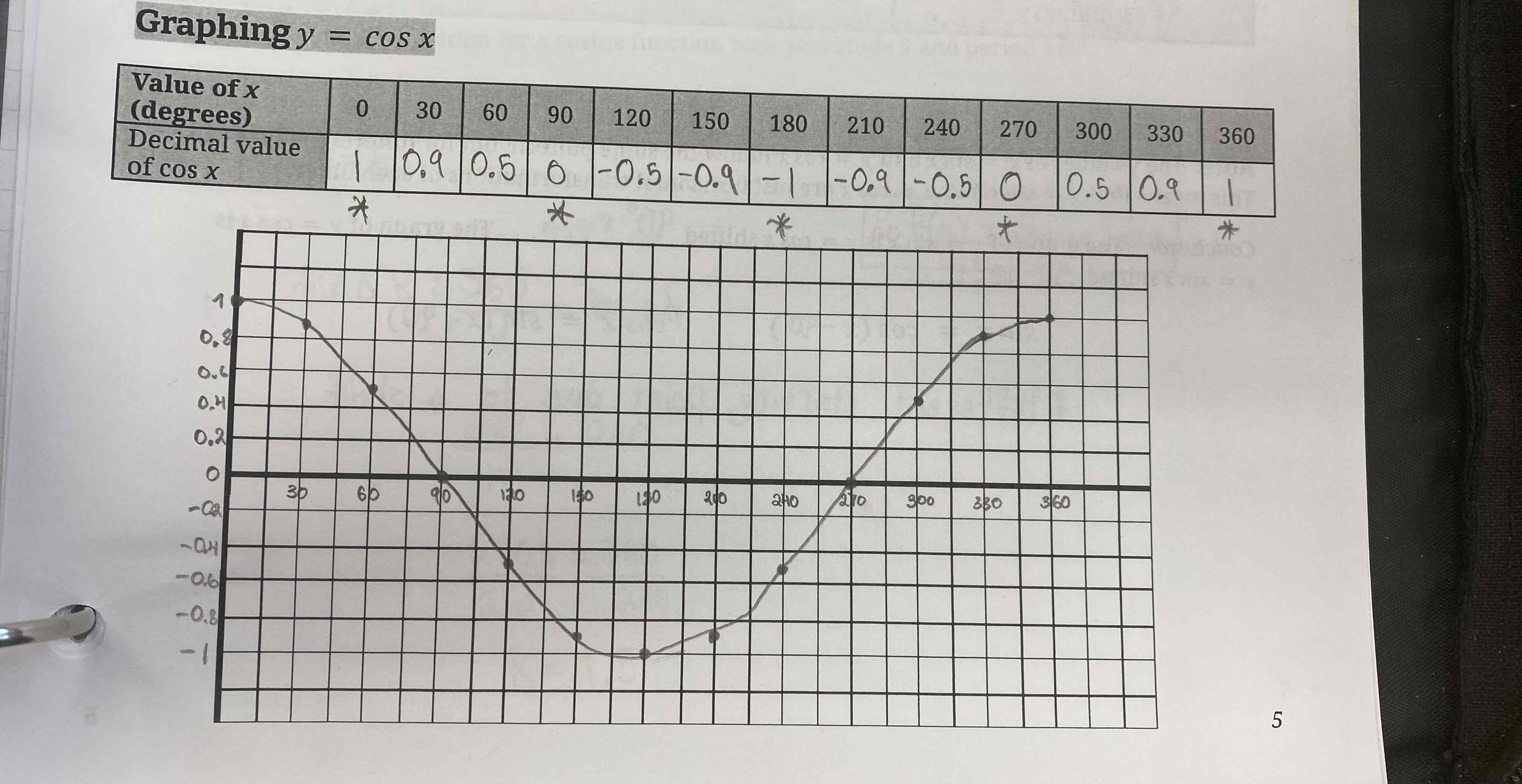
Properties of sine and cosine functions

What are the meaning of the “a” and “k” values of sinusoidal functions

f(x) = a sin k(x)

a: amplitude

k: period: 360/k

Transforming Sinusoidal Functions

y = a sin [k(x - d)] + c

| a | is the amplitude (If negative then reflection in the x-axis)

360/ |k| is the period (If negative then reflection in the y-axis)

d is horizontal shift

c is vertical shift

When doing them all in one first do amplitude and period, then reflections, then shifts

Sequence

A list of numbers arranged in a specific order. They may be finite (end at a certain term value) or infinite (continues to infinity) and denoted by three dots at the end of the list.

Term

Each element of a sequence is called a term. The first term is referred to as t1, and the second term is t2 and so on. The nth term is referred to as tn.

Arithmetic sequence

A sequence that has the same common difference between any pair of consecutive terms. A common difference is obtained by subtracting a term from the previous term. If this value is constant for all terms in the sequence then the sequence is arithmetic. A common difference is denoted by d.

General Term

The general term is a formula to give any term in a sequence just by plugging in n

How to determine a and d/r values from 2 term numbers and their values in a sequence

1. Make an equation using the arithmetic/geometric formula and leave the variables a and d/r

2. Use elimination to subtract or divide out (depending if it is arithmetic or geometric) one of the variables from the equation

3. Solve for the leftover variable

4. Plug in the solved variable into one of the original equations to solve for the other one

Geometric Sequence

Each term is multiplied by the same value each time. You can find the common ratio by dividing any term by the preceding term.

How to determine the number of terms in a sequence given the first 3 terms and last term

Plug in all the values in to the arithmetic or geometric equation and solve for n

If its geometric you will have to get a common base using log on calculator

Recursion Formula

Must have a t1 =

The equation must use tn-1

Series

the sum of the terms of a sequence. The sum of the first n terms of a sequence is Sn where Sn = all of the tn added together.