Linear Motion

What are all the suvat equations?

What are all the suvat equations?

• v = u + at

• s = ut + 1/2at²

• s = 1/2(u+v)t

• v²=u²+2as

s = displacement, m

u = initial velocity, ms^-1

v = final velocity, ms^-1

a = acceleration, ms^-2

t = time, s

What graph are all suvat equations derived from?

This velocity time graph

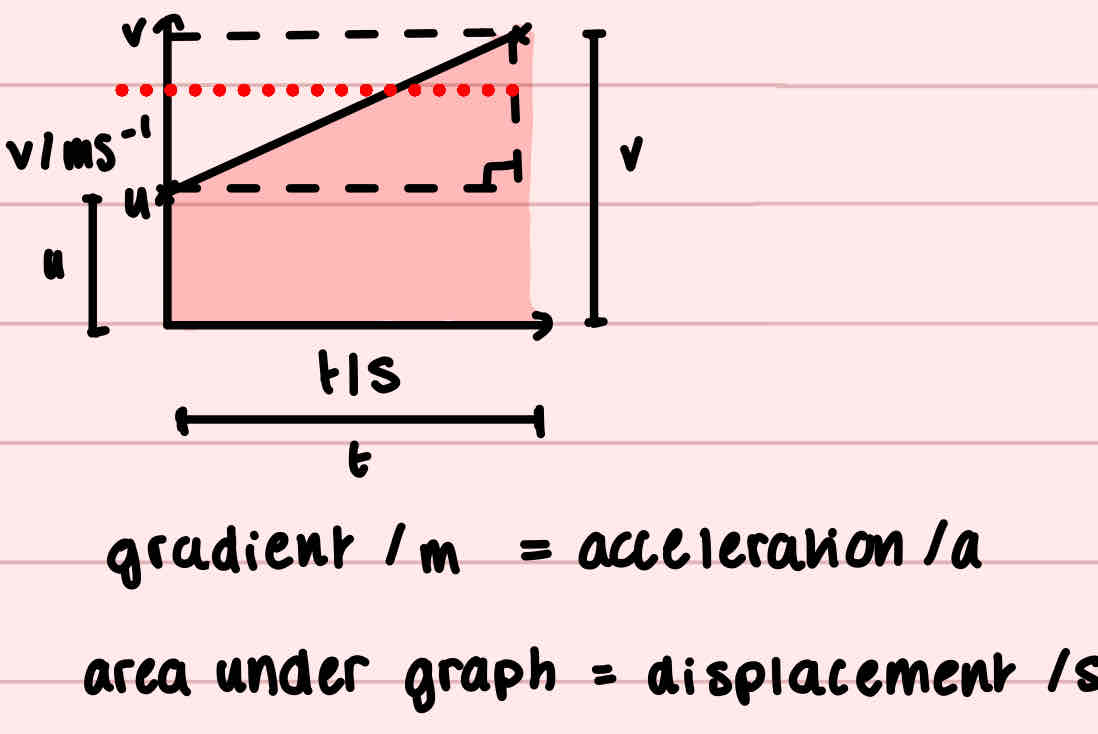
How is the equation without s derived?

Gradient

a = Δv / Δt = v - u / t, xt, +u

v = u + at

How is the equation without v derived?

Area under graph (rectangle and triangle)

Rectangle area = ut

Triangle area = ½ (v-u)t

v = u + at

s = ut + ½ at²

How is the equation without a derived?

Area under graph (trapezium)

½ (a+b)h

½ (u+v)t

How is the equation without t derived?

t = (v - u) / a

s = ½ (v+u) x (v - u) / a x2a

2as = (v+u)(v-u)

v² = u² +2as

What is the acceleration of freefall when an object is falling?

9.81ms^-2

What is the acceleration of freefall/g when an object is rising?

-9.81ms^-2

Describe how to determine the acceleration of freefall

We use a trapdoor and electromagnet/light gates, a steel ball bearing and a data logger.

1) A displacement between the trapdoor and electromagnet/light gates is measured with a metre ruler.

2) The steel ball bearing is dropped from rest. We record the time taken for the ball to travel the entire displacement measured on the data logger. This is repeated 3 times to calculate a mean time for this displacement. We repeat the entire process at regular decreasing displacement intervals.

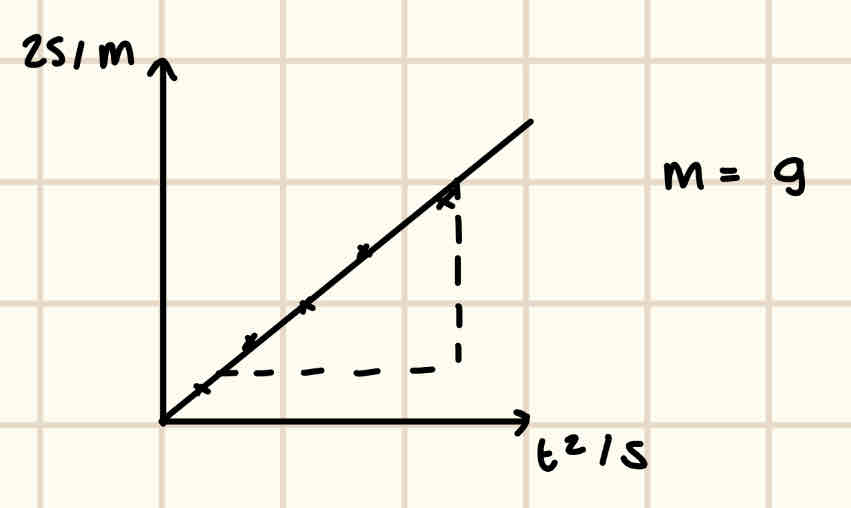
3) We rearrange s = ut + ½ at² to have it in the form y = mx + c where a = g since there’s no external forces acting on the bearing and u = 0 since it’s dropped from rest. We get, 2s = gt².

4) This is the graph:

We draw a line of best fit and the gradient of this line will equal g, m =g