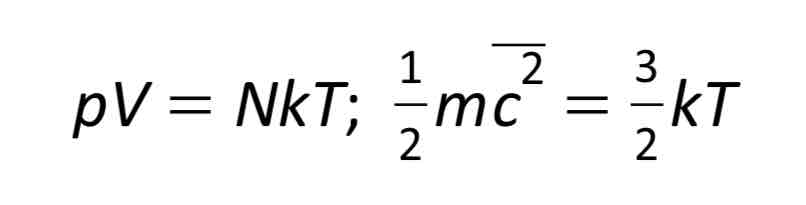Thermal Physics

Thermal Equilibrium

Objects at the same temperature have no net transfer of thermal energy. If one object is hotter than the other, the net flow of thermal energy is from hotter to cooler object until they are the same temperature.

Absolute scale of temperature (ie the thermodynamic scale) that does not depend on property of any particular substance.

The thermodynamic scale uses the triple point of pure water, 273.16K and absolute 0 as its fixed points.

• measured in Kelvin (Which is degrees celcius plus 273.16

Describe the spacing, ordering and motion of solids, liquids and gases. (Aka the kinetic model)

Solids: closely packed together, strong electrostatic forces of attraction between molecules. KE so vibrate around fixed positions. Negative electrostatic potential energy.

Liquids: greater mean separation than solids, more KE so can move around, weaker electrostatic attraction than in solids, less negative electrostatic potential energy

Gases: most KE, elastic collisions causes random speeds and random directions, negligible electrostatic attraction between molecules, maximum electrostatic potential energy of 0J

Brownian motion in terms of kinetic model of matter and a simple demonstration using smoke particles suspended in air.

Demonstrates that molecules of a gas travel in random directions with random velocity. (Smoke particles exhibit random motion because they collide with the air molecules (which are much tinier) which transfers momentum in random ways.

Internal energy

The sum of the random distribution of kinetic and potential energies associated with molecules of a system

Absolute zero

0K, the lowest limit for temperature; the temperature at which a substance has minimum internal energy because no kinetic energy so only electrostatic potential energy. (where all molecules in a substance stop moving completely)

Temperature increase

Temperature rise causes an increase in internal energy

What determines internal energy?

1. Temperature

2. The random motion of molecules

3. The phase of matter

4. Intermolecular forces (determines potential energy) and links to phase of substance

How is internal energy in a system increased? How is it decreased?

Increased:

• doing work on it

• Adding heat to it

Decreased:

• losing heat to its surroundings

• Changing phase (gas to liquid or liquid to solid)

Changes in the internal energy of a substance during change of phase

During phase changes like melting, the temperature remains constant but the change in internal energy is not zero (the heat energy is used to break intermolecular bonds instead of increasing the temperature, so potential energy is still increasing)

Specific heat capacity of a substance

The energy required per unit mass to increase the temperature of 1kg of a substance by 1K.

Estimating specific heat capacity of a substance

The method if mixtures:

1. Known masses of 2 substances at different known temperatures are MIXED together until they reach thermal equilibrium, at which the final temperature is measured.

2. The energy transfer from the hotter substance is the same as the energy transfer from the cooler substance. (Equation used for both sides: E = m x change in temp)

3. If specific heat capacity for one substance is known, it can be used to determine the SHC for the other substance.

An electrical experiment to determine the specific heat capacity of a metal or a liquid

More accurate: use an electrical heater.

1. Known mass of substance is heated by an electrical heater with a known power (or P= IV) for given time (E=Pt).

2. Measure the initial and final temperatures of the substance.

3. Use equations to calculate C.

Make sure you insulate the substance. (Increases accuracy by minimizing external energy transfer).

Specific latent heat of fusion and specific latent heat of vaporisation

E = mL

An electrical experiement to determine the specific latent heat of fusion and vaporisation

Similar to estimating specific heat capacity:

1. Measure mass of substance

2. Heat substance with heater of known power over known time

3. Measure initial and final temperature - and make sure yu measure temperature in between. At some points the temperature remains constant (because the substance is changing shape) - record the duration of these points! This is your time reading.

Amount of a substance in moles

Model of kinetic theory of gases

Assumptions of the model:

• Large number of molecules in random, rapid motion

• Particles (atoms or molecules) occupy negligible volume compared to volume of gas

• All collisions are perfectly elastic and the time of the collisions is negligible compared to the time between collisions

• Negligible forces between particles except during collisions

Pressure (in terms of the model of kinetic theory of gases). Explain pressure in terms of Newtonian theory

Collisions between atoms and wall perfectly elastically = rebound off wall at same speed = changing in momentum is 2mv. (Change in in momentum = F x t) so force exerted on atom by the wall is 2mv/t.

Newton’s third law = every action has an equal and opposite reaction so atom exerts same force back on wall. Total pressure on wall = sum of the force of each collision between atoms in the gas and against the wall and area of the wall.

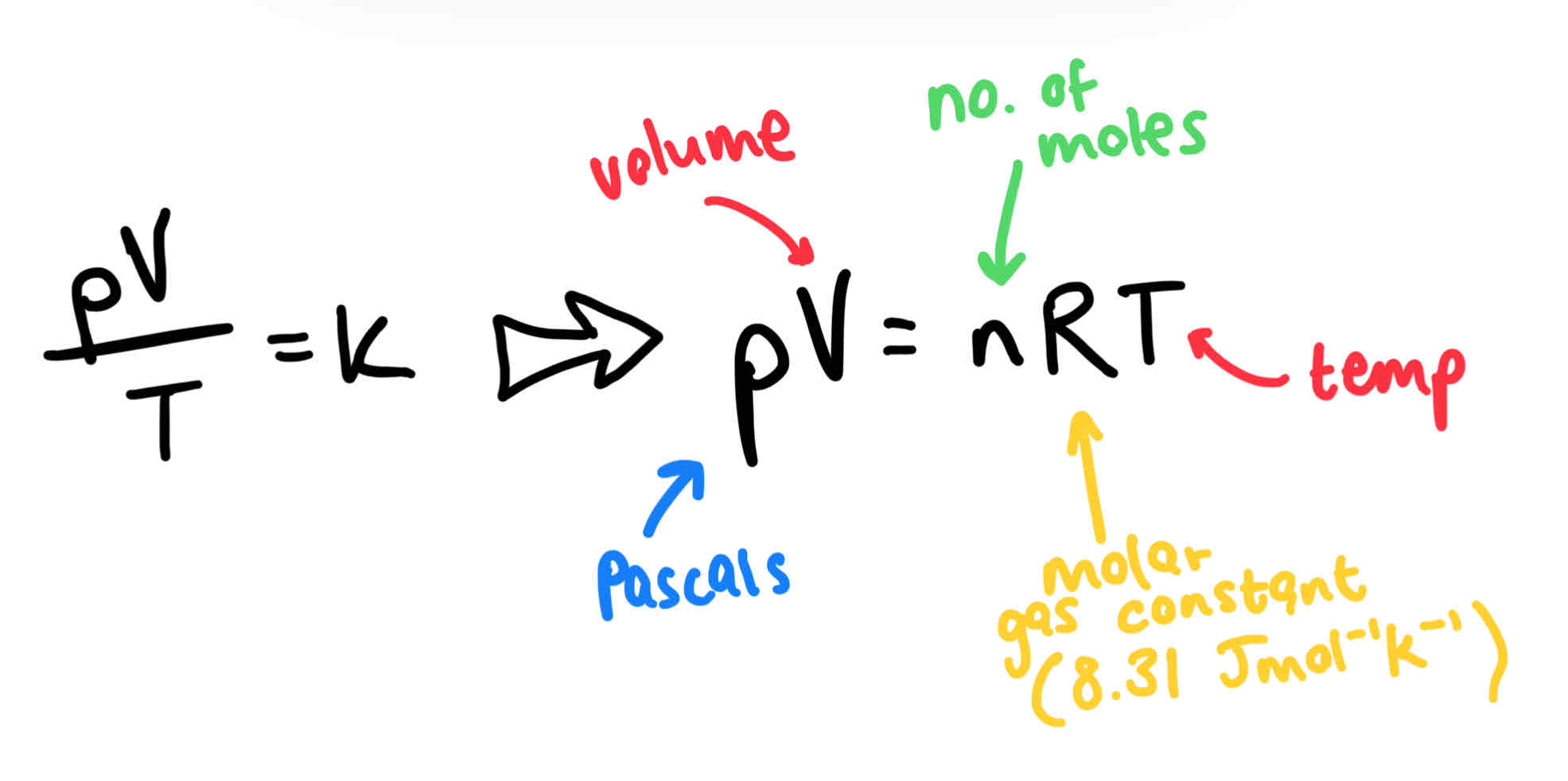
The equation of state of an ideal gas

The 2 ideal gas laws combined:

1. Boyle’s Law: for a fixed mass of gas at a constant temperature, the pressure is inversely proportional to the volume. P = k/V

2. Charles’ law: for a fixed gas at a constant volume, the pressure is proportional to the temperature. P = kT

Techniques and procedures used to investigate PV= constant and P/T = constant

Boyle’s law: PV = constant or P = 1/V

1. Sealed syringe filled with gas and connected to a pressure gauge.

2. Vary the volume of the cylinder using the syringe and record the change in pressure. Lower syringe slowly so no energy is lost as heat in friction (improves accuracy)

3. Plot a graph of P against 1/V

An estimation of absolute zero using variation of gas temperature with pressure.

1. Place a sealed container of air in a water bath (connect the container to a pressure gauge)

2. Vary the temperature of the water bath and record the values of the pressure and temperature.

3. Plot pressure against temperature. (Shows zero kinetic energy of molecules at 0K at x intercept) = no pressure.

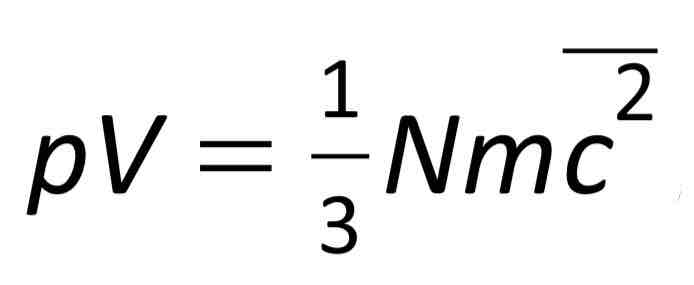
Root mean square speed

Used to find the pressure of a gas at a microscopic level.

Determined by summing the square of all of the individual velocities of molecules, dividing by number of molecules and then finding the square root of this value.

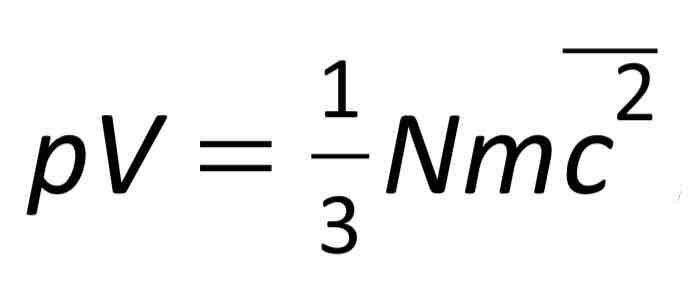
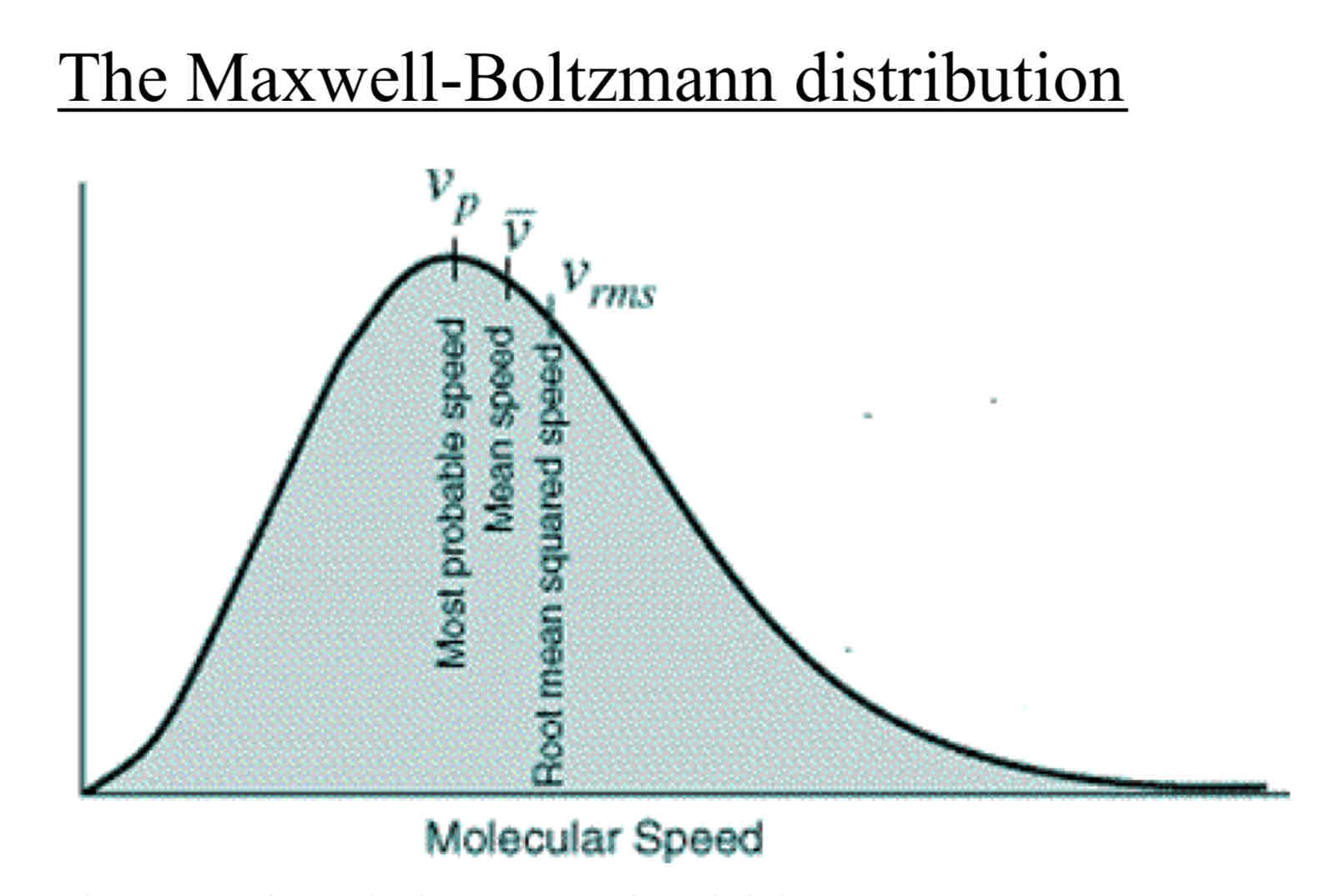
The general characteristics of the Maxwell-Boltzmann distribution

Shows the number of molecules with each speed, against speed c.

The area under the graph represents the total number of molecules

As the temperature of the gas increases, the peak of the graph shifts to a higher speed and the distribution becomes more spread out.

The Boltzmann constant

1.38 × 10 (-23) JK-1.

The Boltzmann constant = molar gas constant (R) divided by Avogadro’s constant (NA)

Used to derive a second equation for the state of an ideal gas: PV= NRT/ NA

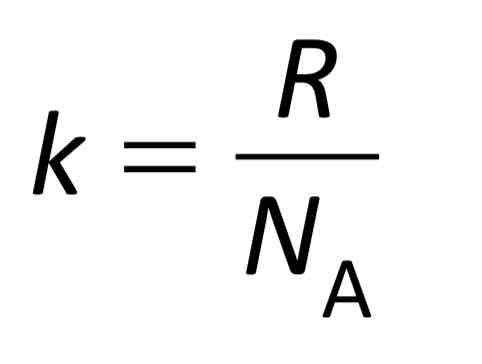
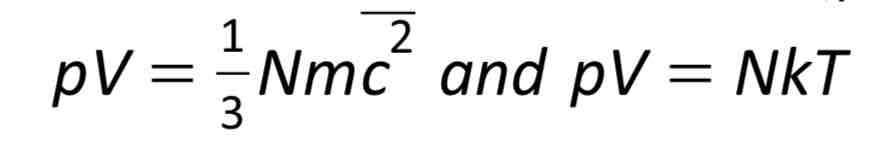
Internal energy of an ideal gas

The sum of the kinetic and potential energies. (No potential energy because there are no electrostatic forces between gas particles.) so internal energy in a gas = kE = which is why internal energy is proportional to temperature.

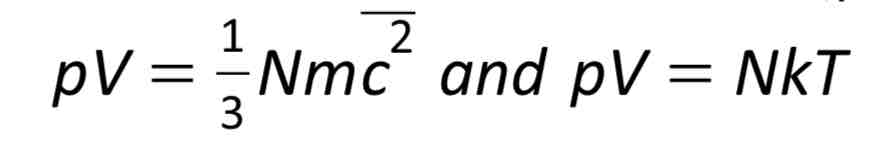
Relate the two equations: