MMW 3.2 - Fractals in Nature

Fractal

• derived from latin word “fractus” meaning fragmented or broken

• a rough/fragmented geometric shape that can be split into parts, each of which is a reduced size copy of the whole (Benoit Mandelbrot)

Characteristics of a Fractal

• Self Similarity

• Fractal Dimension

• Nowhere Differentiable

Self Similarity

Parts have the same form or structure as the whole.

Fractal Dimension

• Associated degree of complexity of shape, structure, and texture of fractals are quantified in terms of fractal dimension

• Measure the space-filling capacity of a pattern that tells how a fractal scales differently than the space in which it is imbedded.

• Does not have to be an integer.

The bigger the fractal dimension-

the more rough is the structure

When a process is repeated over and over, each repetition is called?

iteration

Samples of Geometric Fractals

• Cantor Set

• Sierpinski Triangle

• Sierpinski Carpet

• Menger Sponge

• Koch Snowflake

Cantor Set

• Discovered in 1874 by Henry John Stephen Smith

• Introduced by German mathematician Georg Cantor in 1883

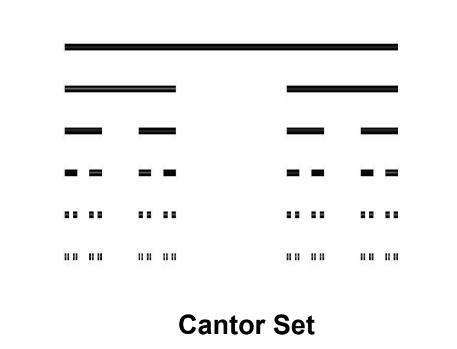
Cantor Set Derivation

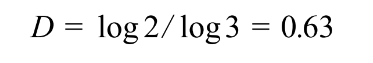
Sierpinski Triangle

• After Polish mathematician Waclaw Sierpinski who discovered and investigated it in 1915

• Dimension: 1.585

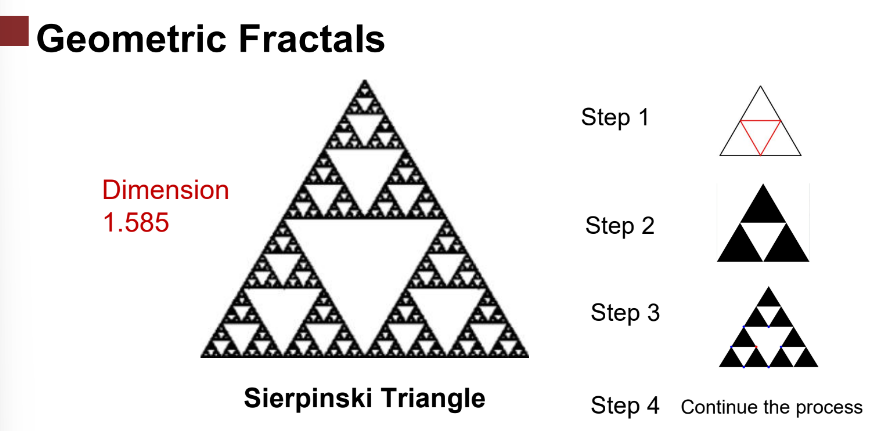
Sierpinski Carpet

• Famous fractal first describe in 1916 by Waclaw Sierpinski (1882-1969)

• Used in designing antennas in cell phones as the number of scales allows for a wide range of receptions

• Dimension: 1.89 (log8/log3)

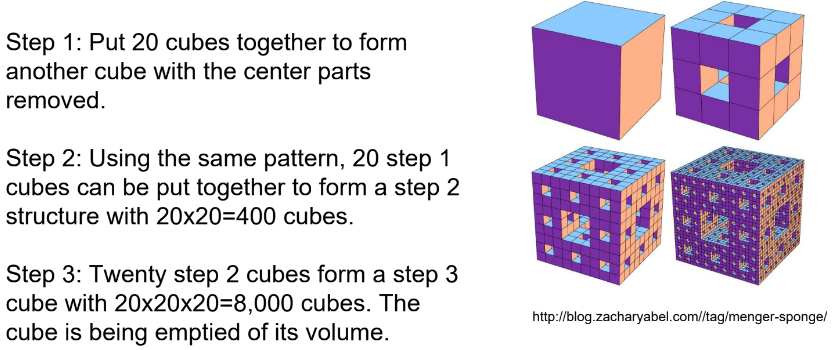
Menger Sponge

• famous fractal solid, 3D equivalent of 1D Cantor Set and 2D Sierpinski Carpet

• First described by Karl Menger in 1926

• Dimension: 2.73 (log20/log3)

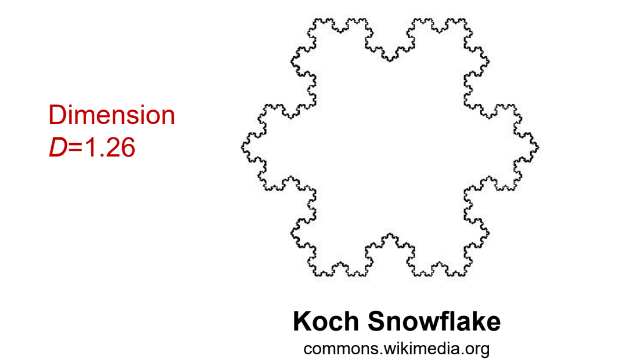
Koch Snowflake

• first appeared in paper published by swedish mathematician Niels Fabian Helge von Kolch in 1996

• Dimension: 1.26 (log4/log3)

Bifurcation

the never-ending process observed in branching algebraic fractals

Fractals in Algebra

• Mandelbrot Set

• Julia Sets

Mandelbrot Set Origin

• Discovered by Benoit Mandelbrot in 1980, responsible for the dev’t of fractal science.

• Discovered shortly after the invention of personal computer and Mandelbrot began his research in IBM

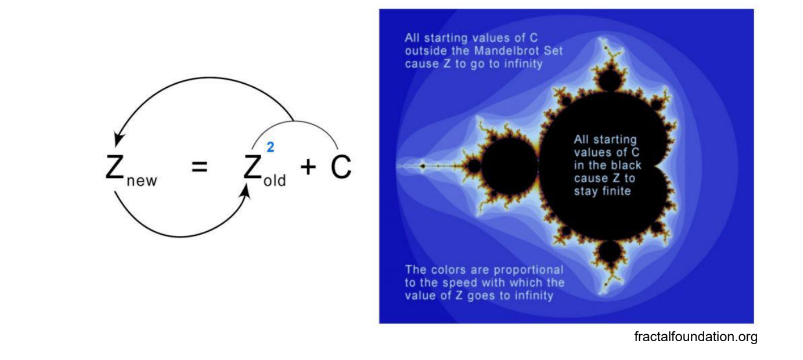
Mandelbrot Set

• Set of points in the complex plane, boundary of which forms a fractal.

• Can be generated using quadratic recurrence equation (Zn+1= Z²n+C)

Julia Sets

• Discovered by Gaston Maurice Julia, closely related to Mandelbrot set

• The iterative function used to produce them is the same as that of the Mandelbrot set (differ only in the way the formula is used)

• In every Mandelbrot, is an infinite number of Julia sets.