MCAT Physics and Math - Waves and Sound

410

sinusoidal waves

individual particles oscillate back and forth with a displacement that follows a sinusoidal pattern; transverse or longitudinal

Transverse waves

the direction of particle oscillation is perpendicular to the propagation of the wave

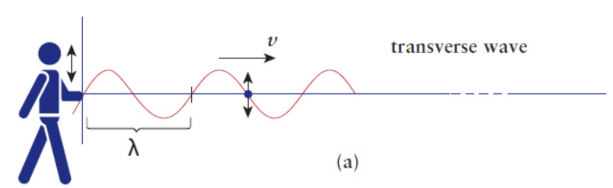
propagation

movement

Longitudinal waves

the particles of the wave oscillate parallel to the direction of propagation

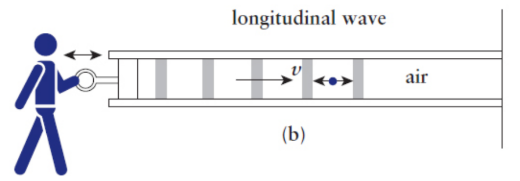
compression

particles closer together

rarefaction/decompression

partices farther apart

crest

maximum of a wave

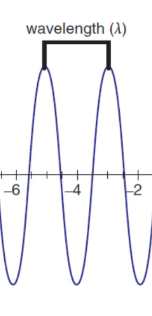
wavelength (λ)

distance from a specific point in the phase of a wave to the next in the same phase, often using the crest/trough

unit: distance (m/cm/nm)

frequency (f)

the number of wavelengths passing a fixed point per second

unit: Hertz (Hz = s^-1)

propagation speed (ν)

ν = fλ

period (T)

number of seconds per cycle

T = 1/f

angular frequency (ω)

scalar measure of the angle per unit time

ω = 2πf

unit: radian/s

equilibrim position.

Waves oscillate about a central point

displacement (x)

describes how far a particular point on the wave is from the equilibrium position, expressed as a vector quantity

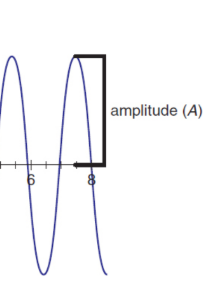
amplitude (A)

maximum magnitude of displacement in a wave; measured from the equilibrium position

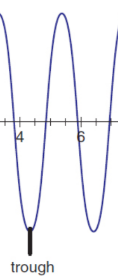
trough

minimum of a wave

phase difference

how well the toughs and crest of two waves that have the same frequency, wavelength, and amplitude and that pass through the same space at the same time align

in phase

crests and troughs coincide; fully constructive interfernece

phase difference = 0

coincide

line up with each other

out of phase

the crests of one wave coincide with the troughs of the other; fully destructive interference

phase difference = λ/2 or 180°

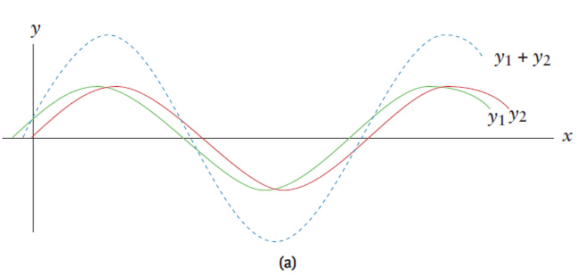
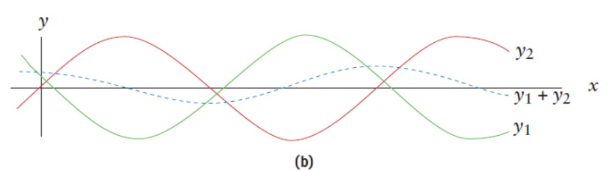
principle of superposition

when waves interact with each other, the displacement of the resultant wave at any point is the sum of the displacements of the two interacting waves

construcive interference.

displacements in the same direction add together; the amplitude of the resultant is equal to the sum of the amplitudes of the two waves

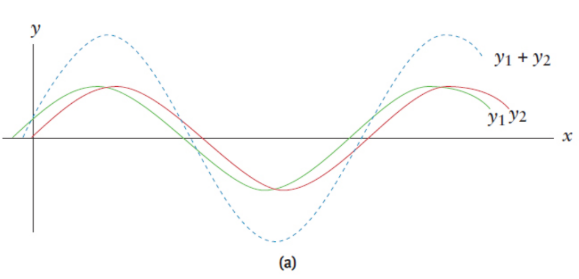
destructive interference

displacements in opposite directions counteract each other; amplitude of the resultant wave is the difference between the amplitudes of the interacting waves

ex. noise-cancelling headphones

traveling wave

move through a medium, transferring energy from one place to another; continuous movement of crests and troughs; no confinement

ex. ocean, sound, light

standing wave

stationary with the only apparent movement of the string is fluctuation of amplitude at fixed points; two waves of same frequency and amplitude travel from opposite directions/reflect back and forth; confined space

ex. instruments with strings, open pipes

nodes

Points in the wave that remain at rest; amplitude is constantly zero

antinodes

Points midway between the nodes fluctuate with maximum amplitude

natural/resonant frequencies

Any solid object, when hit, struck, rubbed, or disturbed in any way will begin to vibrate;can be changed by changing some aspect of the object itself

ex. musical instruments

timbre

quality of the sound; determined by the natural frequency(ies) of the object

noise

resonant frequencies that we do not find particularly musical

fundamental pitch

main resonant frequency

overtones

additional complementary resonant frequencies, related to each other by whole number ratios, producing a richer, more full tone

HUman audible range

frequencies between 20 Hz and 20,000 Hz to healthy young adults, and high-frequency hearing generally declines with age

forced oscillation

periodically varying force is applied to a system, the system will then be driven at a frequency equal to the frequency of the force

force frequency

nearly identical to the swing’s natural frequency

resonating

frequency of the periodic force is equal to a natural (resonant) frequency of the system

damping/attenuation

decrease in amplitude of a wave caused by an applied or nonconservative force

Sound

longitudinal wave produced by the mechanical disturbance of particles in a deformable material along the sound wave’s direction of propagation

speed of sound

v = sqrt(B/ρ)
where B is the bulk modulus, a measure of the medium’s resistance to compression (gas < liquid < solid), and ρ is the density of the medium

spped of sound in air @ 20°C

343 m/s

vocal cords

pair of thin membranes stretched across the larynx, vibrates to make sound

Adult male vocal cords are often larger and thicker than those of adult females; thus, male voices are commonly lower in pitch

pitch

perception of the frequency of sound; proportional

infrasonic

Sound waves with frequencies below 20 Hz

ex. dog whistle

ultrasonic

Sound waves with frequencies above 20,000 Hz

ex. ultrasound

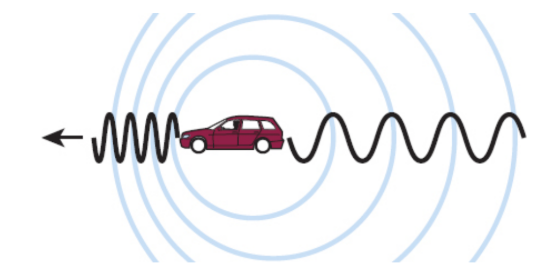
Doppler effect

describes the difference between the actual frequency of a wave and its perceived frequency when the source of the wave and the wave’s detector are moving relative to one another; closer, higher/bluer

Doppler equation

where f′ is the perceived frequency, f is the actual emitted frequency, ν is the speed of sound in the medium, νD is the speed of the detector, and νS is the speed of the source

the upper sign should be used when the detector or source is moving toward the other object; the lower sign should be used when the detector or source is moving away from the other object

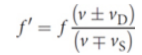
echolocation

the animal emitting the sound (usually a dolphin or bat) serves as both the source and the detector of the sound; how long it takes for the sound to return and the change in frequency of the sound can be used to determine the position of objects in the environment and the speed at which they are moving

shock wave

while traveling at or above the speed of sound; highly condensed wave front; cause physical disturbances as it passes through other objects

sonic boom

passing of a shock wave creates very high pressure, followed by very low pressure

Mach 1

point at which the speed of sound is exceeded

loudness/volume

the way in which we perceive its intensity

Intensity

average rate of energy transfer per area across a surface that is perpendicular to the wave; power transported per unit area

I = P/A

where P is the power and A is the area

I ∝ Amplitude²

units: W/m²

softest audible sound: 10^-12 W/m²

loudest audible sound: 10 W/m²

Instant perforation: 10⁴ W/m²

sound level (β)

logarithmic scale of sound intensity

β = 10 log I/I₀

where I is the intensity of the sound wave and I0

is the threshold of hearing

β_f = β_i + 10 log I/I₀

units: decibels (dB)

Beat Frequency

When two sounds of slightly different frequencies are produced in proximity, as when tuning a pair of instruments next to one another, volume will vary at a rate based on the difference between the two pitches being produced

f_beat = |f₁ - f₂|

Closed boundaries

do not allow oscillation and that correspond to nodes

Open boundaries

allow maximal oscillation and correspond to antinodes

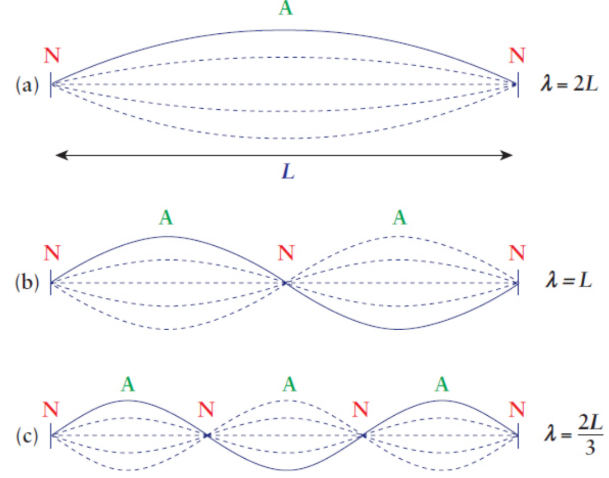
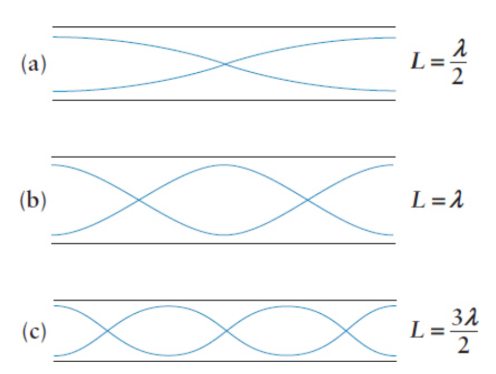
String waves

equation that relates the wavelength λ of a standing wave and the length L of a string

λ = 2L/n

where n is a positive nonzero integer (n = 1, 2, 3, and so on) called the harmonic.

harmonic

corresponds to the number of half-wavelengths

supported by the string

f = nv/2L

fundamental frequency (first harmonic)

lowest frequency (longest wavelength) of a standing wave that can be supported in a given length of string

first overtone or second harmonic

frequency of the standing wave given by n = 2; one-half the wavelength and twice the frequency of the first harmonic

harmonic series

All the possible frequencies that the string can support

open pipes

pipes open on both ends

same harmonics as string

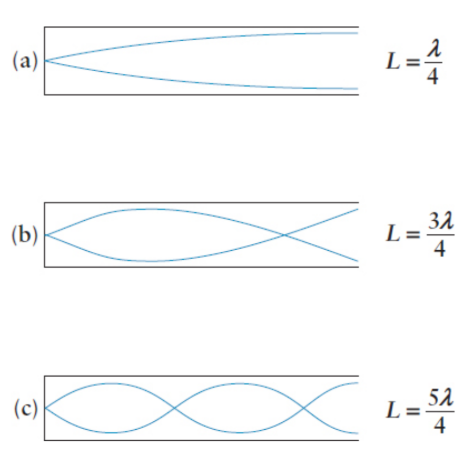
closed pipes

pipes closed at one end

λ = 4L/n

f = nv/2L

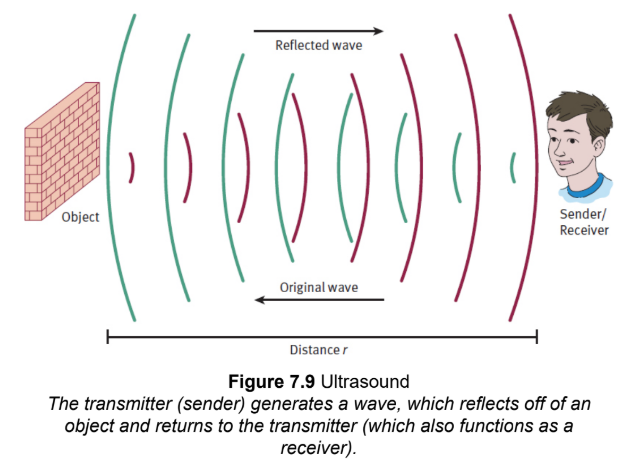
Ultrasound

uses high-frequency sound waves outside the range of human hearing to compare the relative densities of tissues in the body

Doppler ultrasound

used to determine the flow of blood within the body by detecting the frequency shi that is associated with movement toward or away from the receiver.