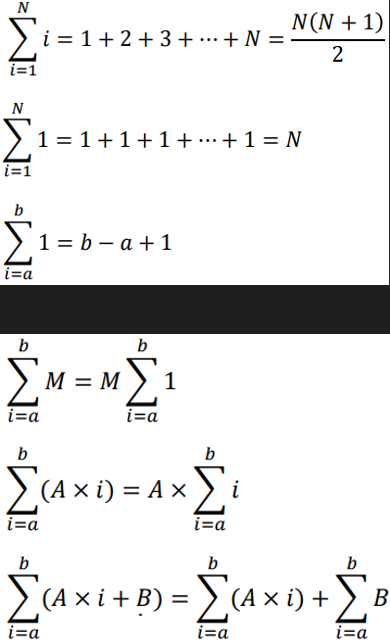Operation Counting

Running Time

depends on the size and the organization of the input

generally, we seek upper bounds (worst case)

Limitations of Experimental Studies

• The algorithm must be implemented, which may take a long time and could be very difficult

• Results may not be indicative for the running time on other inputs that are not included in the experiments

• In order to compare two algorithms, the same hardware and software must be used

• Solution: 

  • Actual runtime can be estimated

  • We will analyse algorithms, and come up with classes of runtimes based on input size

Running Time

depends on the size and the organization of the input

generally, we seek upper bounds (worst case)

Limitations of Experimental Studies

• The algorithm must be implemented, which may take a long time and could be very difficult

• Results may not be indicative for the running time on other inputs that are not included in the experiments

• In order to compare two algorithms, the same hardware and software must be used

• Solution: 

  • Actual runtime can be estimated

  • We will analyse algorithms, and come up with classes of runtimes based on input size

Cost of Operations

• To determine how long an algorithm takes to run we can count-up all the operations it executes

• Let’s first consider what counts as one operation?

• Want to be able to analyse the algorithm itself, independent of the choice of language used to execute

Operations and Instructions

Operations in a high-level language may require many machine-level instructions

However, we ignore minor details 

Operation Counting Example

• The first thing we will do is count how many operations (ignoring minor details) this code executes

• Given an array of integers arr of size n:

int maxel = arr[0];
for (int i = 0; i < n; i++) {
	if (arr[i] >= maxel) {
		maxel = arr[i];
	}
}

• The first line of this code requires 1 operation:

  • As we are ignoring minor differences in implementation

• This operations is always required by the algorithm, regardless of the value of ‘n’ 

• The for loop initialization code also has to always run

• This gives us two more operations: 

  • an assignment (‘i = 0’) and a comparison (‘i < n‘)

  • These will run before the first for loop iteration

• After each for loop iteration, we need two more operations to run,

  • an increment of ’i’ (i.e. ‘i++’) and

  • a comparison (‘i < n’) to check if we'll stay in the loop 

  • Question: How many times do we go around the loop?

• So, if we ignore the loop body, the number of operations this algorithm needs is 3 + 2n

  • 3 operations at the beginning of the for loop

  • 2 operations at the end of each iteration of which we have ’n’ 

• Now, looking at the for body

• We have an array lookup operation and a comparison that always happen

• But the if body may run or may not run, depending on what the array values are

• If it happens to be so that ’arr[i] >= maxel’, then we'll run an additional operation: maxel = arr[i]

• So, we cannot define T(n) easily, because our number of operations doesn't depend solely on the size of input n but also on the organization of the input

  • For example, for arr = [ 1, 2, 3, 4 ] the algorithm will need more operations than for arr = [ 4, 3, 2, 1 ]

For Loop - General Rule

The number of times the instruction within a for loop is executed is given using a general rule

Care: to use this general rule the for loop must be in the above format

Worst Case Analysis (Mostly used)

• In the worst-case analysis, we calculate the upper bound on the running time of an algorithm

• We must know the case that causes a maximum number of operations to be executed

Best Case Analysis (Rarely used)

• In the best-case analysis, we calculate the lower bound on the running time of an algorithm

• We must know the case that causes a minimum number of operations to be executed

Average Case Analysis (Rarely used)

• In average case analysis, we take all possible inputs and calculate the computing time for all of the inputs

• Sum all the calculated values and divide the sum by the total number of inputs

Sentinel Search

A type of Linear search where the number of comparisons is reduced as compared to the linear search

Linear vs Sentinel Search

both have linear time complexity (worst case)

sentinel search requires executing less instructions

Growth Rate of Functions

(use to compare operation counting answers to find most efficient algorithm)

Summation Formula