linear algebra, unit 7

Symmetric Matrix

• A matrix is symmetric if …

• A = A^T

Orthogonal matrix

• a set of orthonormal vectors

• if orthogonal then… A^-1=A^T

Spectral theorm

• A symmetric mxn matrix “A” has the following properties

• A) “A” has n real eigen values

• B) if you had an eigen value with multiplicity k, you are guarunteed the k corresponding vectors exist

• C) the eigenvectors in the eigenspace are orthogonal to eachother

• d) “A” is orthogonally diagonizible

Quadratic form

• you can turn a quadratic equation into the form

• x^TAx

(A is a symmetric matrix)

Building matrix “A” for a quadratic form

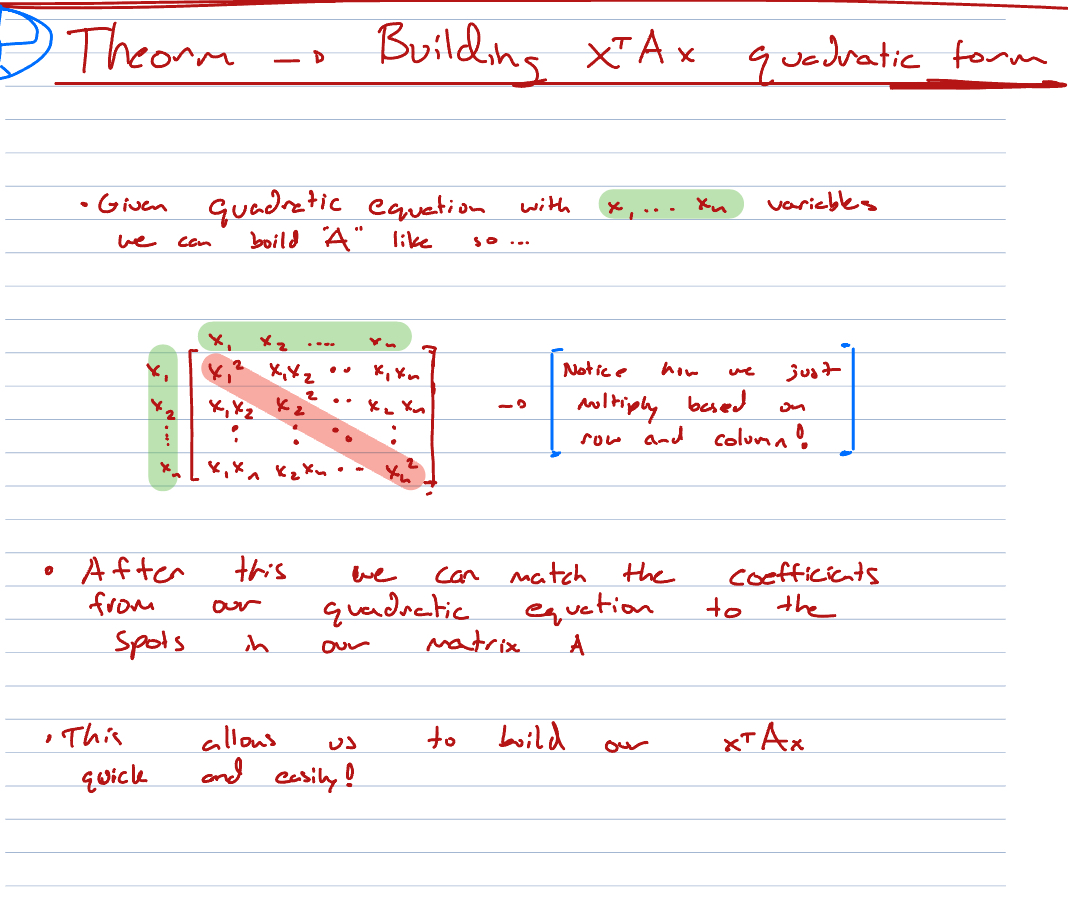
quadratic form classification

Principle Axes theorm(with proof)

Building Single value decomposition

• A=UΣV^T

Σ

• “not necessarily square” diagnosable matrix

• values along it diagonal are decreasing in order and are the square root of the eigenvalues of A^TA

V^T

• We take the eigenvalues (before square rooting them) and turn them into a set of normalized eigenvectors

• We then transpose the matrix(make sure order is proper)

U

• Created by multiplying AV and then turning the columns into unit vectors (V is the set of the eigenvectors before they are normalized)