FInance 4030 Exam I

the Federal Reserve does all of these but which one of the following?

a) Insures Deposits

b) Conducts Monetary Policy

c) Supervises and regulates bank activities

d) serves as the commercial bank for the U.S. Treasury

e) Operates check clearing and wire transfer facilities

a) insures deposits

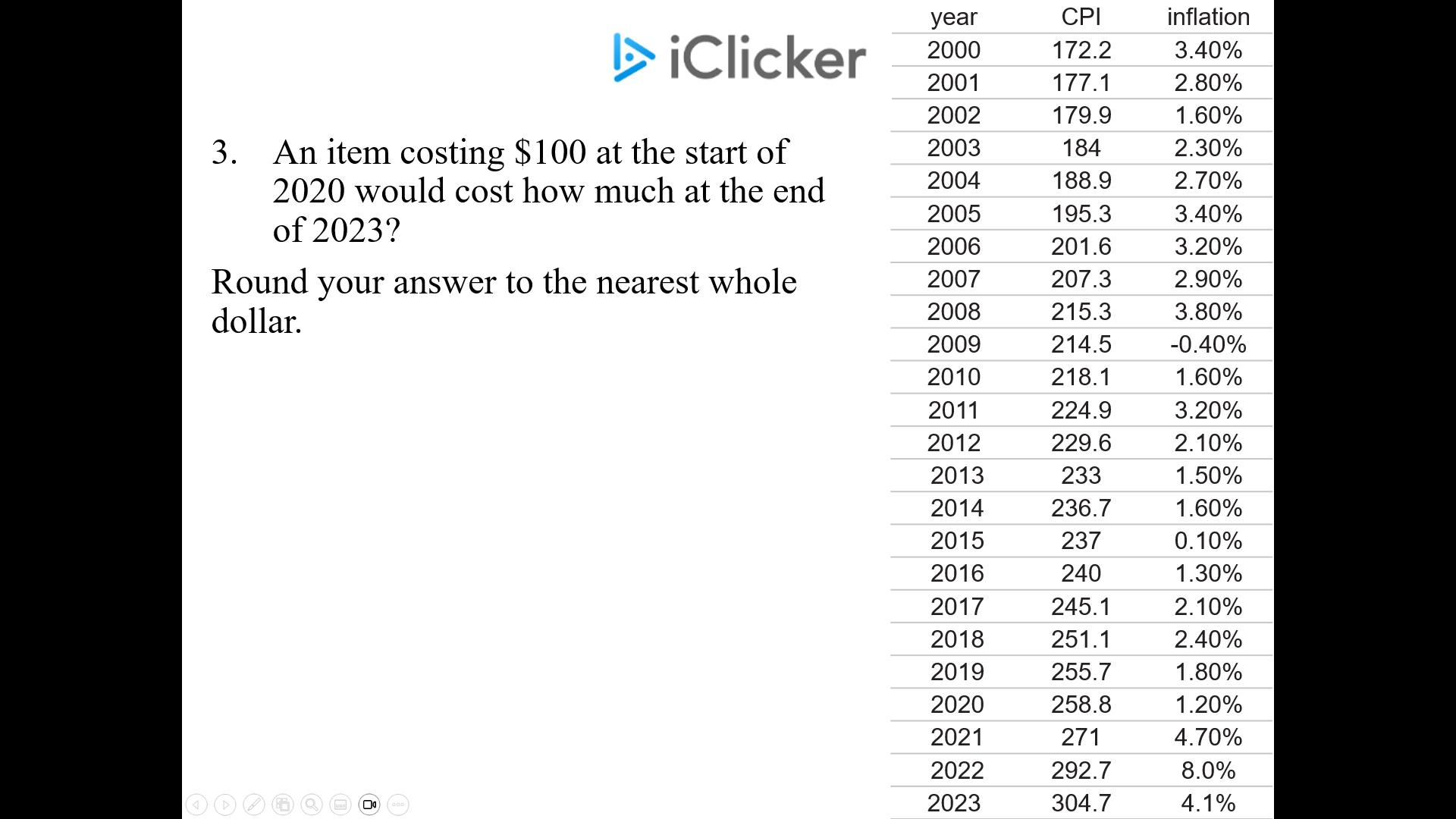
An item costing $100 at the start of 2020 would cost how much at the end of 2023? Round to the nearest dollar

$119 = $100 × 1.012 × 1.047 × 1.08 × 1.041

Calculate the realized return on a 6% APR bond with a semiannual payments and a remaining maturity of 10 years. You purchased the bond 6 years ago at par on a coupon payment and just sold it at par immediately after receiving a coupon payment.

6% → N = 12, P/Y = 2, PV = -1000, PMT = 30, FV = 1000

CPT I/Y → 6.00%

What is the primary tool that the Fed uses to meet its monetary policy

Open Market Operations

How many months will it take to pay off a $9,000 loan with monthly payments of $225? The APR is 18% (round to nearest whole number)

62

Explanation:

N → ??, P/Y=12, I/Y = 18, PV = 9000, PMT = 225, FV = 0

CPT N = 61.54

You have just graduated with $65,000 in student loans. The interest rate is a record-low 2.8 percent APR. and the repayment cells for ten years of monthly payments, the first payment is at the end of the first month. How big are your payments?

621.66

Explanation:

N = 120, P/Y = 12, I/Y = 2.8 , PV = 65000, CPT PMT = -621.66

What rate of return is offered by an investment that costs $5,000 today, and pays $2,000 per year at the end of the year, for three years?

9.7

Explanation:

2 options to figure it out.

1. CF 5000 ±

   ↓ 2000

   ↓3 Enter

   IRR CPT = 9.7

2. N = 3 , P/y = 1, Pv= -5000, PMT = 2000, CPT PMT = 2000

You are considering buying an annuity that promises to pay $1,200 per month for the next 30 years (the first payment due at the end of the first month). If you can earn 8% APR on other investments of similar risk, what is the most that you would be willing to pay for this annuity today?

N = 360, P/Y = 12 , I/Y = 8, PMT = 1200, CPT PV = $163,540.20

You have just won $5000 playing the lottery. You are goign to save this for your retirement in 30 years. If your investment yields 12% how much will you have saved for your retirement?

N = 30, I/Y= 12, PV = 5000, CPt FV = $149,799.61

You have saved $20,000 as a down payment on a $100,000 house. Mortgage rates at 5.5% APR with monthly compounding. If you finance for 15 years, what will be the amount of your monthly payment?

653.67

N = 180, P/Y = 12 , I/Y=5.5 , PV = 80000, CPT PMT = -653.67

You have just signed a lease for a car. You will make monthly payments for 60 months as well as an end-of-lease payment of $2,500. Each payment is due at the START of the month. The first payment is due today. If the interest rate is 6% APR and the car is worth $30,000, calculate the monthly payment.

N = 60, P/Y = 12, I/Y = 6 , PV = 30,000 [BGN] ← 2nd BGN 2nd Set CPT PMT, FV = -2500

CPT PMT = -541.44

You have incurred $45,000 in student loans, to be repaid monthly for 10 yars at 5% APR. Your intention is to pay an extra $50 per month each month. How many months will it take until you are out of debt?

106

N = 120, P/Y = 12, I/Y = 5 , PV = 45000, CPT PMT = -477.29 → PMT - 50 - -527.29 (Use as new PMT), CPT N = 105.68 → 106 Months

What rate of return is offered by a retirement plan where you invest $2000 per year for the next 10 years (the first payment is due today) and receive $250,000 in one payment 30 years from today?

10.24

CF0 = 2000 ±

C01 = 2000 ±

F01 = 9

C02 = 0

F02 = 20

C03 = 250,000

IRR CPT = 10.24

You want to retire in 40 yrs with $1,000,000 You can earn 12% APR on your investments. If you save $180 per month (first payment at the end of the first month) how long will you have to save to meet this goal?

64

Step One:

N = 480, P/Y = 12, I/Y = 12, Pmt= 0 , FV = 1,000,000, CPT PV = -8,428.31

PV = -8,428.31 → 2nd Round ± PV

Step two:

FV = 0, PMT = 180 ±, I/Y= stays the same, PV = 8428.31, CPT N = 63.47

Check work:

N = 63.47 [STO] [2]

I/Y = 12

PV = 0

PMT = 180 ±

CPT FV = 15,849.33 [±][PV]

N = 480 - [RCL][2] = 416.53

I/Y = 12

PV = -15,849.33

PMT = 0

CPT FV = 1,000,000

During your retirement, starting 40 years from now and lasting 30 years, you want to have monthly income of $5,000. If you anticipate earning 8% on your savings, how much should you start saving per month? Your first payment is at the end of this month.

195.19

Step one: N = 360, P/y = 12, I/Y = 8, PMT = 5000, FV = 0, CPT PV = -681,417.47

CPT PV = -681,417.47 [2nd] [Round] [±][FV]

STEP 2

FV = 681,417.47, N= 480, I/Y = 8, PV = 0 , CPT PMT = -195.19

Three years ago, you bought a mini cooper, financing the $30,000 purchase price for five years with a 6% APR loan and monthly payments. You have just made your 36th payment and are considering the purchase of a Chrysler PT Cruiser. How much do you owe on your loan?

Step one

N = 60, P/Y = 12, I/Y = 6 , PV = 30,000 , FV = 0 , CPT PMT = -579.98

PMT = -579.98 [2nd][Round][PMT]

Step two

PMT =579.98, N = 36, I/Y = 6, PV = 30,000 , CPT FV = -13,086.26

You have $50,000 in student loans: $20,000 is financed at 5% APR with monthly payments over 10 years.

$30,000 is financed at 24% APR with monthly payments over 10 years.

what is the interest rate on your portfolio of debt?

17.14

Step one :

N = 120, P/Y = 12, I/Y = 5 , PV = 20,000, CPT PMT = -212.13 [2nd][Round][STO][1]

Step 2

N = , I/Y = 24, PV = 30,000 , CPT PMT =-661.44 [+] [RCL][1] [=] [2nd][Round][PMT]

Step 3

PMT = -873.57, N = , PV = 50,000, CPT I/Y = 17.14

You are considering refinancing your house. Exactly 10 years ago you borrowed $150,000 at 9% APR agreeing to make 360 monthly payments. you have just made your 120th payment. Interest rates have dropped from 9% to 6%. You want to refinance with a 20-year loan at 6%. By how much would your monthly payment decline?

245.87

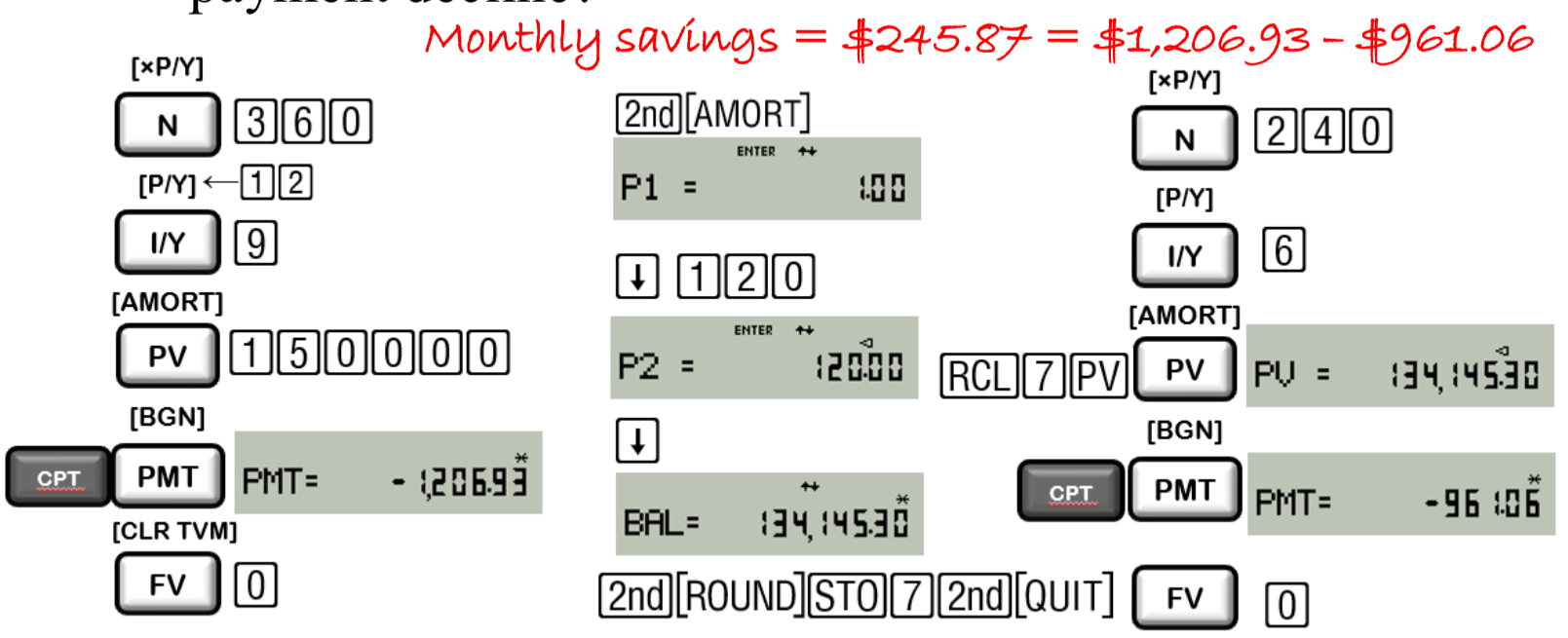
you just graduated with $65,000 in student loans. The interest rate is a record low 2.8% APR, and the repayment calls for ten years of monthly payments, the first payment is at the end of the first month. Now, let’s compute the real-world last payment.

621.89

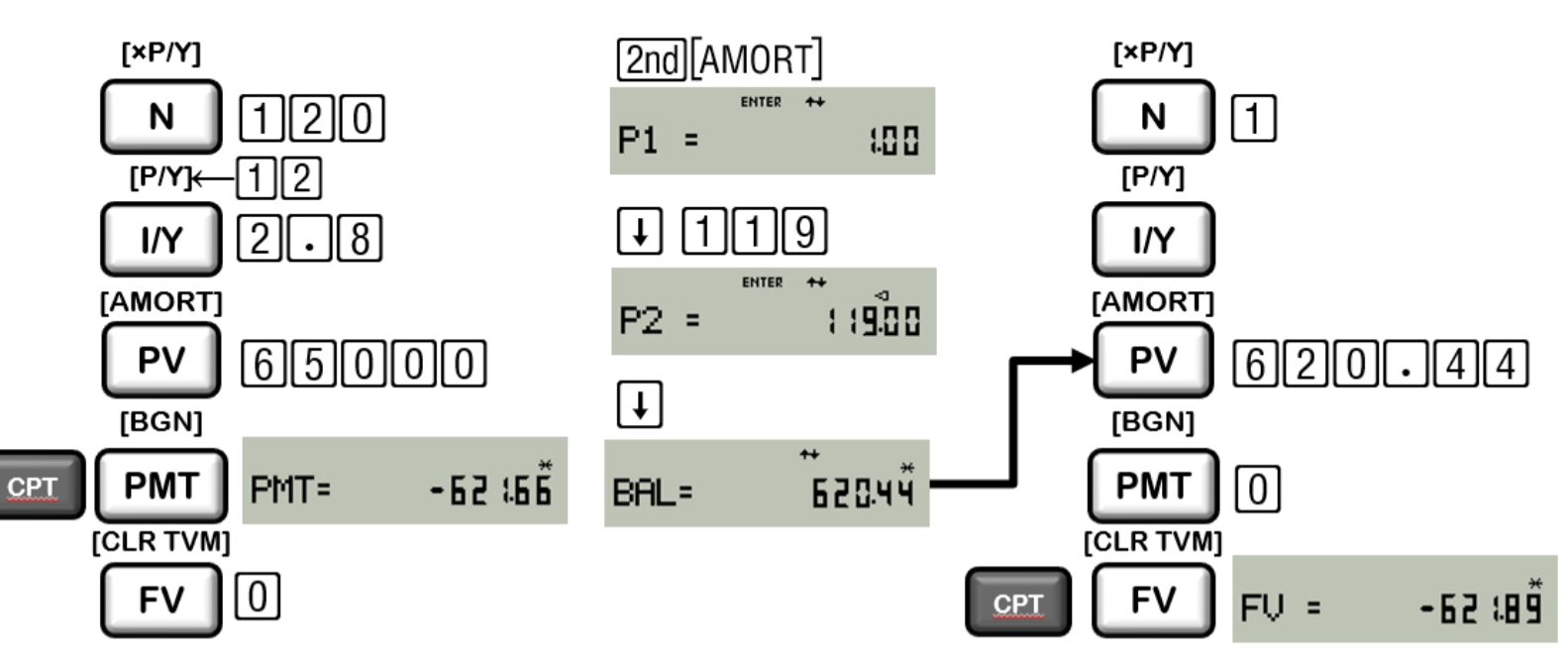
How long is years and motnhs will it take to pay off a $13,500 credit card balance with monthly payments of $485? The APR is 26.5%

Answer: 3 years 8 months

Explanation:

P/Y = 12, I/Y = 26.5 , PV = 13,500 , PMT = 485, FV = 0

CPT N = 43.66

You are considering buying an annuity that promise to pay $5,500 annually for the next 10 years (the first payment due at the end of the first year).

If you pay $35,000 to purchase this annuity calculate the annual rate of interest you earn on this investment.

9.19

N = 10, CPT I/Y, PV = 35,000 , PMT = 5,500, FV = 0

you have just graduated with 40,000 in student loans

The interest rate is 3% APR and the repayment calls for 10 years of monthly payment and the first payment is at the end of the month.

N = 120, P/Y = 12, I/Y = 3, PV - 40,000, CPT PMT = 386.24

you are considering buying a bond that promises to pay 30 euros semi annually for the next 30 years, The par value is 1,000 euros and it just paid a coupon payment.

If the yield to maturity is 9.5% APR on other bonds of similar risk, what is the most that you would be willing to pay (in euro) for this bond today?

the straight bond value is 723.14 euros

N = 30, P/Y = 2, I/Y = 9.5 , PMT = 30,000 , FV = 1,000, CPT PV = 723.14

You have just received $8,500 as graduation gifts. You are going to save this for a down payment on a house in 5 years, as well as adding $250.00 per month starting at the end of the first month. If your investment yields 12.5 percent APR how much will you have saved (in dollars and cents) for your down payment?

N = 5*12 → 60, P/Y=12, I/Y=12.5, PV=8500, PMT=250.00

CPT FV = $36,522.02

Calculate the effective annual interest rate for a 5.5% APR loan with semiannual compounding and a 6-year maturity.

2 ND ICONV = 5.5 APR

EFF= 5.58

You bought a house, financing $400,000.00 for 30 years with a 6 percent APR loan and monthly payments. Calculate, to the penny, the real-world last payment on this loan.

$2,400.30

step one

N = 360 , P/Y = 12, I/Y = 6.00% , PV = 400,000 , FV = 0 , PMT = -2398.2

after a hypothetical 359 payments of $2398.2 we have a remaining balance of $2388.36

Amort P1 = 1.00, P2 = 359 , Balance 2,388.36

N = 1 , I/Y = 6.0%, PV = -2,388.36, PMT = 0, CPT FV = $2400.30

Calculate the real-world last payment on a $50,000 student loan amortized monthly over 10 years at 5% APR.

529.94

Step one

N = 120, P/Y = 12, I/Y = 5, PV = 50,000 , FV = 0 , CPT PMT = -530.33

Step two

Amort P1=1, P2 = 119, Balance = 527.74

Step three:

N = 1 , I/Y=5, PV = 527.74, PMT = 0 , CPT FV =529.94

Calculate the dollar-based return of a US investor who sank $10,000 into shares of British Telecom one year ago at £116.05 and just sold at £135.85 today the GBP is at $1.3196 and one year ago the exchange rate was $1.2602

22.58

Explanation

1. 10,000 / 1.2602 = 7,935.25

2. 7,935.25 / 116.05 = 63.378

3. 63.378 × 135.85 = 9289.13

4. 9289.13 × 1.3196 = 12,257.94

5. (12,257.94-10,000)/10,000= 0.2258 or 22.58%

Calculate the dollar-denominated return for an investor who one year ago (January 2023) starts with $10,000, converts to British pounds at $1.24/£ buys shares of British Petroleum at £475.25. He sells today at £451.00 and converts to USD at $1.27/£

A) -3%

B) 3%

C) 30%

A ) -3%

Explanation:

(10,000/1.24)/475.25 = 16.97 → (16.97 × 451.00)*1.27= 9,719.91

(9,719.91 - 10,000)/(10,000) = -0.0028 → -3%

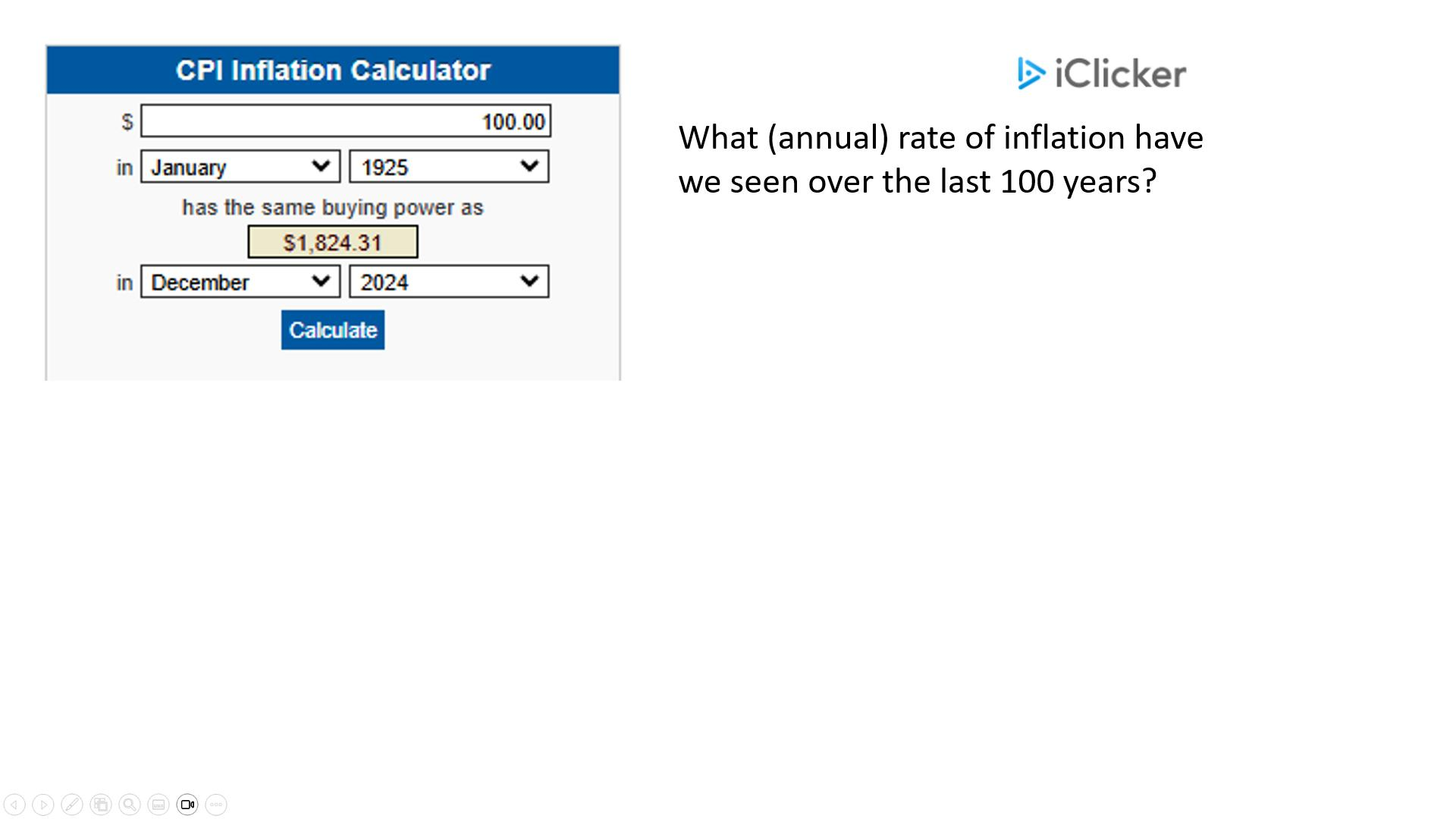
What is the annual rate of inflation we have seen over the last 100 years?

01/1925 → $100

Buying power as of 12/24 → 1,824.31

2.95

Explanation

N = 100, P/Y = 1, PV = -100, FV = 1824.31 CPT I/Y = 2.95

Consider a bond that pays a semi-annual coupon payment of $30 twice a year. The remaining maturity it 5 years. The par value is $1,000. If the bond just sold for $985, calculate the YTM of this bond

6.35

N = 10 , P/Y = 2, PV = - 985 , Pmt = 30 , FV = 1000, CPT I/Y = 6.35

Consider a bond that pays a quarterly coupon payment of $25 four times a year. The remaining maturity is 5 years. The par value is $1,000. If the the YTM of the bond is 3% calculate the price of this bond.

1323.98

N = 20, P/Y = 4, I/Y = 3, PMT = 25, FV = 1000, CPT PV = 1323.89

On Monday 3/3/25 you buy a treasury bond. The bond pais semi annual payments of $30 every july 1 and january 1, compute the accrued interest due the seller of the bond at settlement on tuesday March 4, 2025.

10.28 (look up)

Calculate the annual rate of inflation in the US from August 2000 to August 2025

August 2020 → 100.00

August 2025 → 124.65

4.51 %

N = 5 , P/Y = 1, PV = -100 , FV = 124.65 , CPT I/Y = 4.51%

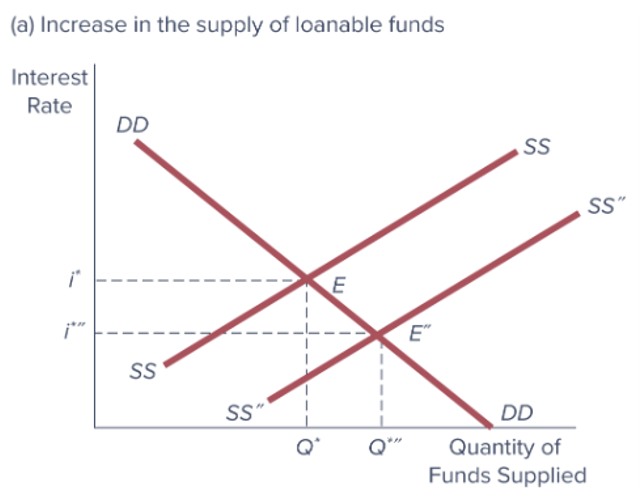
Which of the following would normally be expected to result in an increase in the supply of funds, all else equal?

I. the perceived riskiness of all investments decreases

II. Expected inflation increases

III. Current income and wealth levels increase.

IV. Near term spending needs of households increase as energy costs rise.

I and III only

Inflation causes the demand curve for loanable funds to shift to the _____ and causes the supply curve to shift to the ______.

Right, Left

An individual actually earned a 4% nominal return last year. Prices went up by 3 % over the year. Given that the investment income was subject to a federal tax rate of 28% and a state and local tax rate of 6%, what was the investor’s actual real after-tax rate of return?

-0.36%

Explanation:

(0.04 (1- (.28 + 0.06) )) - 0.03 = -0.0036

On Janaury 25, 2024, the existing or current (spot) one=year, two-year, three-year, and four year zero coupon Treasury security rates were as follows:

₁R₁ = 2.17% , ₁R₂= 2.39% , ₁R₃=2.43% , ₁R₄ = 2.54%

₁R_N = Actual N-period rate today

Using the unbiased expectations theory, calculate the one-year forward rate on zero-coupon Treasury bonds for year two as of January 25, 2024

2.61%

Two Options:

₂F₁ = [(1+₁R₂)²/(1+₁R₁) - 1

=[(1+0.0239)²/(1+.0217)]-1 = 2.61%

OR TVM Calculator

Step one

N = 1, P/Y = 1, I/Y = 2.170, PV = -1000 , PMT = 0, CPT FV = $1,021.70

Step two

N = 2, I/Y = 2.390, PV = -1000 , PMT = 0 , CPT FV = 1,048.37

Step three

N = 1 , PV = 1021.70, PMT = 0, FV = 1048.37, CPT I/Y = 2.610%

On Janaury 25, 2024, the existing or current (spot) one=year, two-year, three-year, and four year zero coupon Treasury security rates were as follows:

₁R₁ = 2.17% , ₁R₂= 2.39% , ₁R₃=2.43% , ₁R₄ = 2.54%

₁R_N = Actual N-period rate today

Using the unbiased expectations theory, calculate the TWO-year forward rate on zero-coupon Treasury bonds for year two as of January 25, 2024

2.690%

step one

N = 2, P/Y = 1, I/Y = 2.39, PV = -1,000 , PMT = 0 , FV = 1,048.37

step two

N = 4, I/Y = 2.540 , PV = -1000, PMT = 0 , FV = 1,105.54

step three

N = 2 , PV = 1048.37 , FV = 1105.54, CPT I/Y = 2.690%