Unit IV (4) - Laplace Transform Analysis of CT Signals + LTI Systems

Laplace Transform (LT)

a frequency domain technique in which signals are represented as a sum of exponentially-varying sinusoids of different complex frequencies (e^st)

Unilateral LT

begins at 0- (ignores minus time) it is most suitable for “causal signals”; system property not signal property but using it to describe a signal

For a given x(t)

finite integral does not exist for all s; implies a “region of convergence (ROC) in the s-plane;

Existennce of the Unilateral LT (ULT)

any signal that grows no faster than an exponential; ROC (for “causal signals”) is thus always always to the right of a vertical line at some s=sigmao in the s-plane

Can a signal that blows up have an LT?

as long it is not faster than an exponential sso exponentials can have an LT

Inverse LT

c is a constant to ensure convergence of the integral; contour integral indicates that the LT indeed represents a CT signal as a sum of exponentally varying sinusoids

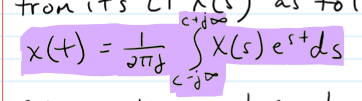
Partial Fraction Expansion (PFE) Approach

1. break LT X(s) fown into simpler components via PFE

2. find the inverse LT of the simpler components via table look-up

3. sum the inverse LTs to arrive at the inverse LT x(t)

only applicable when the LT is a rational function → a ratio of polynomials in s

LT Properties

linearity, time-shifting, frequency-shifting, time-differentiation, time-integration, time convolution, and LCCDEs

Linearity

x1(t) ←> X1(s) + x2(t) ←> X2(s) then ax1(t) + bx2(t) ←> aX1(s) + bX1(s)’ a and b are any constants (linear combination)

Time shifting

x(t) ←> X(s) then x(t-to) ←> e^(-sto) X(s) = e^(-(sigma + jw)to x(s)

x(t) is causal and can be viewed as x(t)u(t) to be more explicit

property is useful for determing the LT of sognals w/ diff. time intervals

Frequency-shifting

x(t) ←> X(s) then x(t)e^(Sot) (exponential-varying sinusoid) ←> X(s-So)

Time-differentiation

x(t) ←> X(s) then dx(t)/dt ←> xX(s) - x(0-)

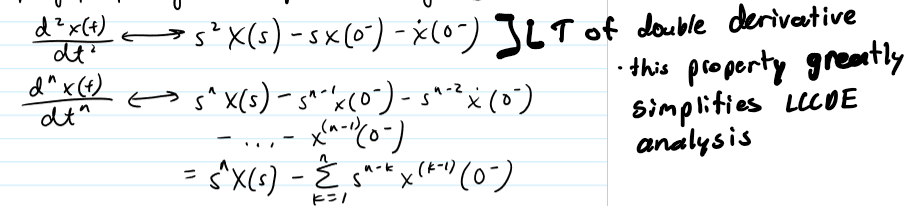
Time Integration

x(t) ←> X(s) then the running integral (integral from 0- to t of x(T) dT ←> X(s)/s

Time Convolution

x1(t) ←> X1(s) + x2(t) ←> X2(t) then x1(t) * x2(t) ←> X1(s) X2(s)

if convolve 2 signals in time, multiply thier LTs

Implication of Time convolution Property

flipping and sliding can be circumuated as follows

1. compute the LT of x(t) to get X(s) and the LT of h(t) to get H(s) (system fcn

2. compute Y(s) = H(s) X(s) (multiplication)

3. take inverse LT of Y(s) to get y(t)

LCCDEs Revisited

time differentiation property of the LT along w/ the PFe approach for determing teh inverse LT make LCCDE analysis easy

Total Response

can be decomposed into ZSR and ZIR; sum ZIR and ZSR to get original this;

ZSR and ZIR

forced response and natural response can be determined from these but not vice versa; they are general

H(s) - the system fcn for an LCCDE

P(s)/Q(s) = Y(s)/X(s); can be inverse transformed to arrive at the impulse response h(t) of an LCCDE

System Function for a CT LTI System

H(s) = Y(s)/X(s) = P(s)/Q(s) = Y{h(t)}; detrmines teh complex scale factor applied by the system to inputs of the form e^(Sot) → y(t) = H(So)e^(Sot)

Q(s)

characteristic polynomial

P(s)

the “input” polynomial

What happens if P(s) and Q(s) have common factors?

roots of the numerator + denominator polynomials of H(s) are NOT the same as the input and characteristic polynomials

Poles

roots of the denominator polynomial; after common factors are canceked (if there is any)

Zeros

roots of the numerator polynomial; H(s) = 0

Pole-Zero Diagrams

indicate the location of the system poles and zeros in the s-plane; pole denoted w/ an X and a zero is denoted w/ an O

A causal system is?

1. BIBO stable if its poles are in the left-half s-plane (LHP)

2. unstable if poles in the RHP

3. marginally stable if there are no poles in the RHP but pole(s) on the jw-axis

ZERO LOCATIONS ARE NOT RELEVANT FOR STABILITY