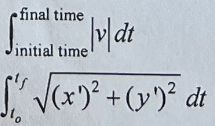AP Calculus BC - Stuff You Must Know
4.5(2)
4.5(2)
Card Sorting
1/59
Earn XP
Description and Tags
This includes a ton of stuff you must remember for the AP Test. It includes equations, theories, rules, derivatives, integrals, and more. I only recommend using these as flashcards or multiple choice only.
Calculus
Differential Equations
AP Calculus BC
Unit 1: Limits and Continuity
AP
Calculus BC
Review
Final
Images
Everything!
Everything
Equations
Theorems
Theories
Rules
Derivatives
Integrals
Slope
Distance
Displacement
Polar
Parametric
Cartesian
Average Value Theorem
Mean Value Theorem
Extreme Value Theorem
Continuity
Final Review
AP Test
11th
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
60 Terms
1
New cards
L'Hôpital's Rule
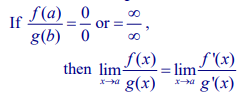
2
New cards
Slope of a Parametric equation
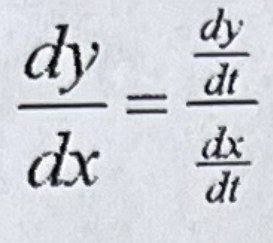
3
New cards
Euler’s Method
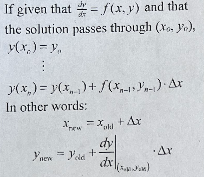
4
New cards
Polar Area
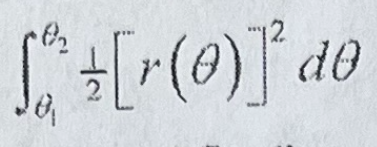
5
New cards
Polar Slope
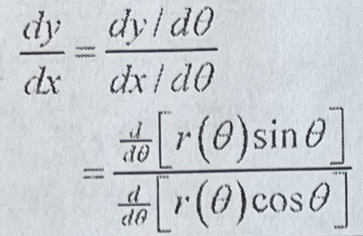
6
New cards
Integration by parts
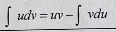
7
New cards
Integral of logarithms
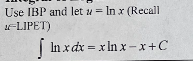
8
New cards
Ratio Test
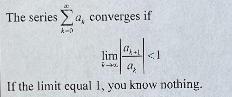
9
New cards
sin(2x)
2sin(x)cos(x)
10
New cards
cos(2x)
cos^2(x) - sin^2(x)
11
New cards
cos(2x)
1 - 2sin^2(x)
12
New cards
cos^2(x)
1/2(1+cos(2x))
13
New cards
sin^2(x)
1/2(1-cos(2x))
14
New cards
sin^2(x) + cos^2(x)
1
15
New cards
1+tan^2(x)
sec^2(x)
16
New cards
cot^2(x) + 1
csc^2(x)
17
New cards
sin(-x)
\-sin(x)
18
New cards
cos(-x)
cos(x)
19
New cards
Taylor Series
f(x) = f(a) + f’(a)(x-a) + \[f’’(a)(x-a)^2 / 2!\] + \[f’’’(a)(x-a)^3 / 3!\] + …
20
New cards
Lagrange Error Bound
\
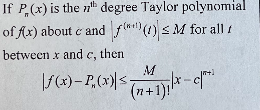
21
New cards
Maclaurin Series
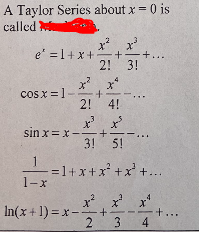
22
New cards
Alternating Series Error Bound
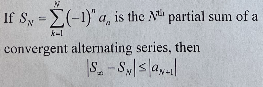
23
New cards
Geometric Series
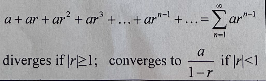
24
New cards
sin(0)
0
25
New cards
cos(0)
1
26
New cards
tan(0)
0
27
New cards
sin(pi/6)
1/2
28
New cards
cos(pi/6)
root3/2
29
New cards
sin(pi/4)
root2/2
30
New cards
cos(pi/4)
root2/2
31
New cards
sin(pi/3)
root3/2
32
New cards
cos(pi/3)
1/2
33
New cards
sin(pi/2)
1
34
New cards
cos(pi/2)
0
35
New cards
Chain Rule
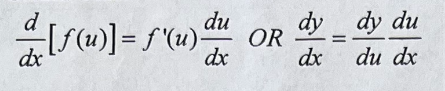
36
New cards
Product Rule
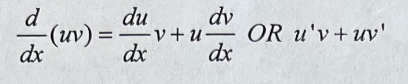
37
New cards
Quotient Rule
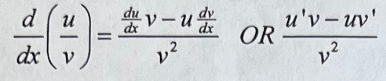
38
New cards
Trapezoidal Rule
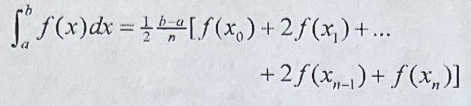
39
New cards
NEVER FORGET (for integrals)
\+C
40
New cards
Average Value
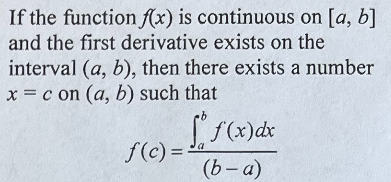
41
New cards
d/dx sin(x)
cos(x)
42
New cards
d/dx cos(x)
\-sin(x)
43
New cards
d/dx tan(x)
sec^2(x)
44
New cards
d/dx cot(x)
\-csc^2(x)
45
New cards
d/dx sec(x)
sec(x)tan(x)
46
New cards
d/dx csc(x)
\-csc(x)cot(x)
47
New cards
d/dx ln(u)
1/u
48
New cards
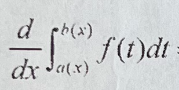
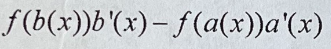
49
New cards
Solid Disk Method
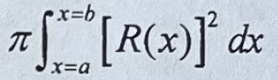
50
New cards
Solid Washer Method
\
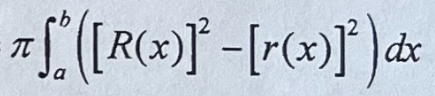
51
New cards
Cartesian Arc Length
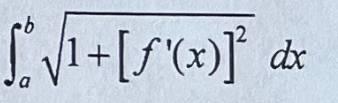
52
New cards
Polar Arc Length
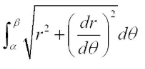
53
New cards
Parametric Arc Length
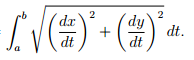
54
New cards
Intermediate Value Theorem
If the function f(x) is continuous on \[a,b\], then f(x) achieves every value between f(a) and f(b) in the open interval (a,b).
55
New cards
Mean Value Theorem
If the function f(x) continuous on \[a,b\], and the first derivative exists on the interval (a,b), then there is at least one number x = c in (a,b) such that f’(c) = \[ f(b)-f(a) \] / (b-a).
![If the function f(x) $$continuous on \[a,b\], and the first derivative exists on the interval (a,b)$$, then there is at least one number x = c in (a,b) such that f’(c) = \[ f(b)-f(a) \] / (b-a).](https://knowt-user-attachments.s3.amazonaws.com/a559904ffac24820b04928c7ae6b6bda.jpeg)
56
New cards
Rolle’s Theorem
Same as mean value theorem but if f(a) = f(b), then there is at least one number x = c in (a,b) such that f’(c) = 0.
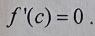
57
New cards
d/dx loga(x)
1/xln(a)
58
New cards
Displacement
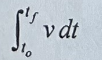
59
New cards
Speed
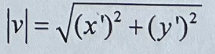
60
New cards
Distance