Chapter 21: Capacitance

Capacitor

An electrical component

• Comprises two metal plates separated by an insulator

• Stores charge

Storing Charge

When capacitor is connected to a cell

• Electrons briefly flow from cell

• Cannot travel between plates because of insulating material

• Very brief current means:

  • Electrons are removed from first plate (acquires positive charge)

  • Electrons deposited to second plate (acquires negative charge)

• Current is equal throughout circuit, so charge is conserved:

  • plates have equal but opposite charge Q⁺ and Q^-

• Current falls to zero when p.d across plates = e.m.f of the cell

  • Capacitor is fully charged

Capacitance

Charge stored per unit p.d across a capacitor

• C = Q / V

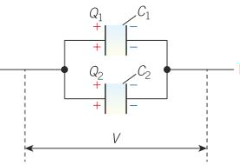
Capacitors in Parallel

• p.d across each capacitor is the same

• Charge is conserved → Total charge = Sum of individual charges

• Total Capacitance = C₁ + C₂ + C_3^…

Capacitors in Series

• Kirchoff’s Second Law→p.d across the combination = sum of individual p.d’s = V₁ + V₂ + V₃…

• Charge stored by each capacitor is the same

• Total capacitance is given by 1/C₁ + 1/C₂ + 1/C₃ …

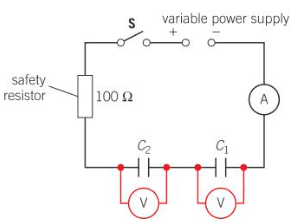
Investigating Capacitance

• Circuit diagram is set up, with capacitance of each capacitor known

• Switch closed → Current is briefly registered but quickly settles to zero

  • Electrons move in circuit only until capacitor is fully charged

• V₁ and V₂ of each capacitor can be taken from the voltmeters

• Changing the fixed resistor has no effect on the charges stored

Energy stored by a capacitor

• Work is done to overcome the electrostatic forces from the electrons on the negatively charged plate

• This pushes an electron from the positively charged plate to the negatively charged plate,

• This is provided by the battery

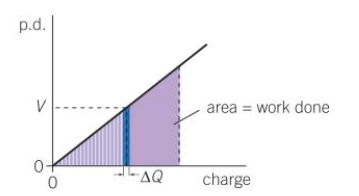
Potential Difference-Charge graphs

• x-axis: Q

• y-axis: V

• Area = Energy stored

  • W = ½ QV

Energy equations

• W = ½ QV

• W = ½ V²C

• W = ½ Q² / C

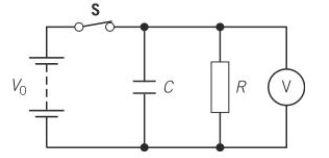
Discharging a Capacitor

• Switch is initially closed and capacitor is fully charged

• When switch is opened at t = 0:

  • V across the capacitor = V₀

  • Current in resistor = V₀ / R

  • Charge stored in capacitor = V₀C

• capacitor discharges

  • Charge stored decreases with time

  • Thus, V decreases with time

  • Thus, Current in resistor decreases with time

• Eventually V and Q of Capacitor and I in resistor = 0

V/Q/I against time

• V = V₀e^-t/CR

• I = I₀e^-t/CR

• Q = Q₀e^-t/CR

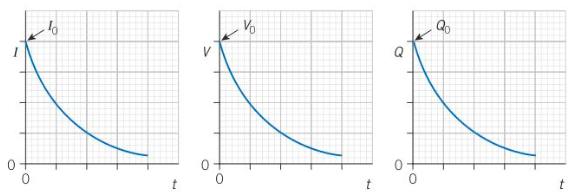
Time Constant

• CR = Capacitance x Resistance

• Same units as time

• Time it takes for V/Q/I to decrease to e^-1 of its initial value

Modelling exponential decay

• Q = VC → V = Q/C

• I = V/R →I = (Q/C) / R

  • I = V/R = Q/CR

• I = -ΔQ/Δt = -Q/CR

  • Q = Q₀e^-t/CR is a solution for the equation

Iterative modelling

Use equation ΔQ/Δt = -Q/CR

• Start with Q₀ and known value for CR

• Choose a time interval, Δt, which is very small compared to CR

• ΔQ = Δt/CR x Q → Charge leaving capacitor

• Q - ΔQ = charge left in capacitor → Sub into equation again

• Repeat for subsequent multiples of the time interval Δt

Charging Capacitors

• Switch is closed, Capacitor charges up

• Potential Difference across Capacitor increases

• Kirchhoff’s 2nd law →V_c + V_R = V₀

  • Thus, as V_C increases, V_R decreases’

• Current decreases exponentially

• After a long time (depending on CR), Capacitor is fully charged

  • potential difference of Capacitor = V₀

  • V_R = 0

  • At this point, I = 0

Current / p.d in a charging capacitor

• I = I₀e^-t/CR

Since V = IR

• V_R = V₀e^-t/CR

Since V₀ = V_C + V_R

• V₀ = V_C + V₀e^-t/CR → V_C = V₀ - V₀e^-t/CR

• V_C = V₀(1 - e^-t/CR)