Discrete Math Flashcards

Vocabulary flashcards for review.

Recursive Algorithm

An algorithm that reduces a problem to an instance of the same problem with smaller input.

Euclidean Algorithm

A method for computing the greatest common divisor of two nonnegative integers a and b with a < b using reduction: gcd(a,b) = gcd(b mod a, a) and the condition gcd(0,b) = b when b > 0.

Merge Sort

Works by iteratively splitting a list into two sublists of equal length until each sublist has one element and each sublist is represented by a balanced binary tree. At each step a pair of sublists is successively merged into a list with the elements in increasing order.

The Product Rule

A procedure that can be broken down into a sequence of two tasks. There are n1 ways to do the first task and n2 ways to do the second task. Then there are n1∙n2 ways to do the procedure.

The Sum Rule

If a task can be done either in one of n1 ways or in one of n2 ways, where none of the set of n1 ways is the same as any of the n2 ways, then there are n1 + n2 ways to do the task.

Subtraction Rule

If a task can be done either in one of n1 ways or in one of n2 ways, then the total number of ways to do the task is n1 + n2 minus the number of ways to do the task that are common to the two different ways.

Division Rule

There are n/d ways to do a task if it can be done using a procedure that can be carried out in n ways, and for every way w, exactly d of the n ways correspond to way w.

Tree Diagrams

A method to solve counting problem, where a branch represents a possible choice and the leaves represent possible outcomes.

The Pigeonhole Principle

If k is a positive integer and k + 1 objects are placed into k boxes, then at least one box contains two or more objects.

The Generalized Pigeonhole Principle

If N objects are placed into k boxes, then there is at least one box containing at least ⌈N/k⌉ objects.

Permutation

An ordered arrangement of a set of distinct objects.

Cartesian product

In set theory, it is the set of all ordered pairs (a, b) where a is in A and b is in B.

Binary Relations

A binary relation R from a set A to a set B is a subset R ⊆ A × B.

Reflexive Relations

R is reflexive if (a,a) ∊ R for every element a ∊ A.

Symmetric Relations

R is symmetric if (b,a) ∊ R whenever (a,b) ∊ R for all a,b ∊ A.

Antisymmetric Relations

A relation R on a set A such that for all a,b ∊ A if (a,b) ∊ R and (b,a) ∊ R, then a = b is called antisymmetric.

Transitive Relations

A relation R on a set A is called transitive if whenever (a,b) ∊ R and (b,c) ∊ R, then (a,c) ∊ R, for all a,b,c ∊ A.

Composition

Suppose R1 is a relation from a set A to a set B and R2 is a relation from B to a set C. Then the composition (or composite) of R2 with R1, is a relation from A to C. if (x,y) is a member of R1 and (y,z) is a member of R2, then (x,z) is a member of R2∘ R1.

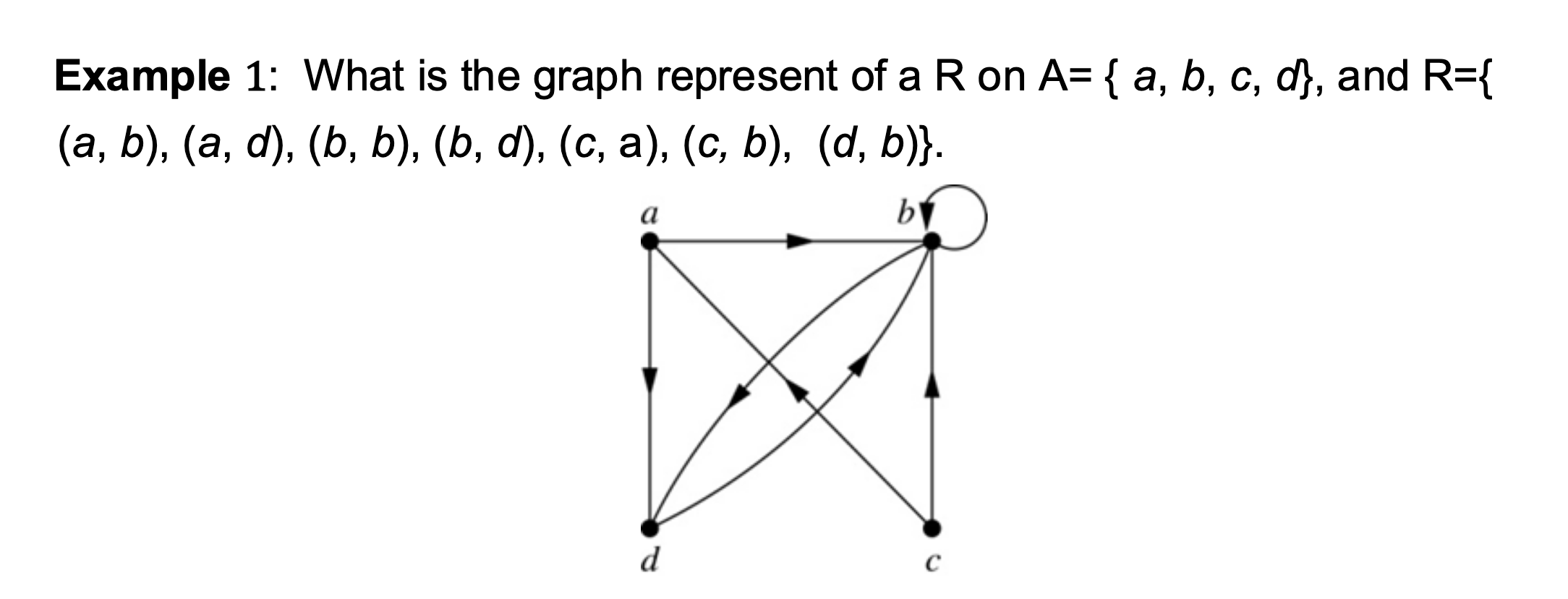
Directed graph

A directed graph, or digraph, consists of a set V of vertices (or nodes) together with a set E of ordered pairs of elements of V called edges (or arcs). The vertex a is called the initial vertex of the edge (a,b), and the vertex b is called the terminal vertex of this edge.

Equivalence Relations

A relation on a set A is called an equivalence relation if it is reflexive, symmetric, and transitive.

Equivalence Class

Let R be an equivalence relation on a set A. The set of all elements that are related to an element a of A is called the equivalence class of a.

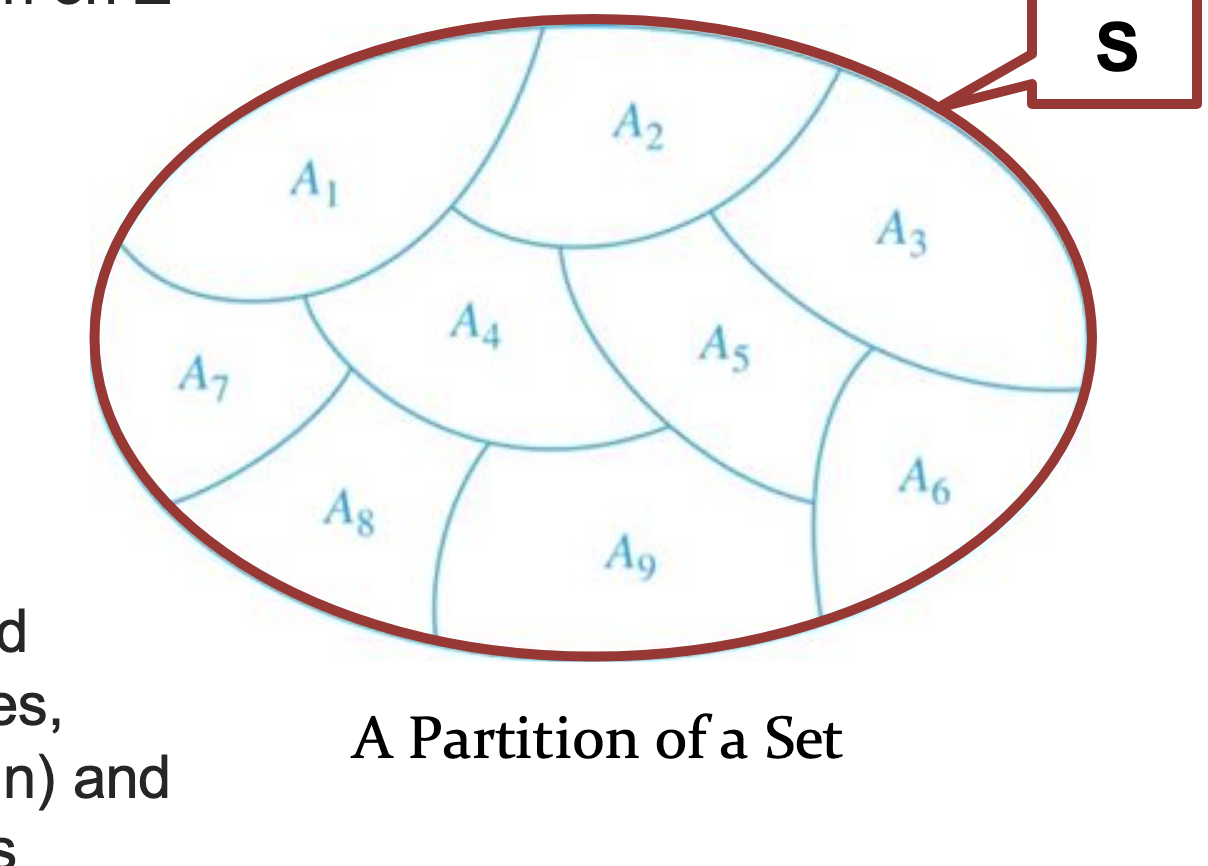
Partition of Set

A partition of a set S is a collection of disjoint nonempty subsets of S that have S as their union.

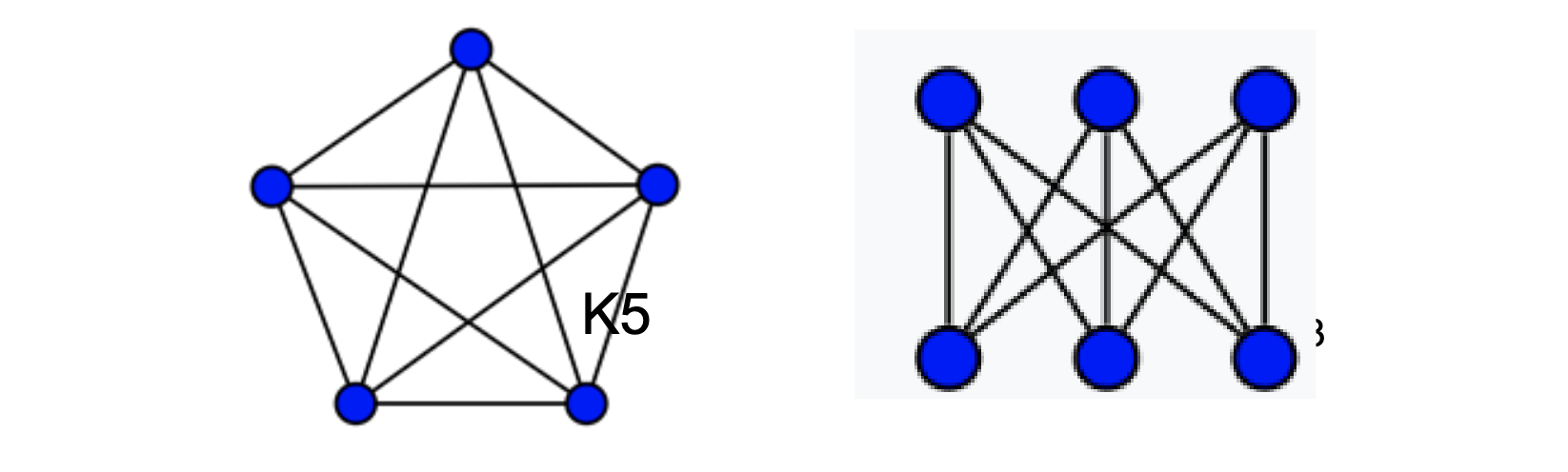
Planar Graph

A graph that can be drawn on the plane without edge crossings.

Graph Traversal

The process of visiting each vertex in a graph.

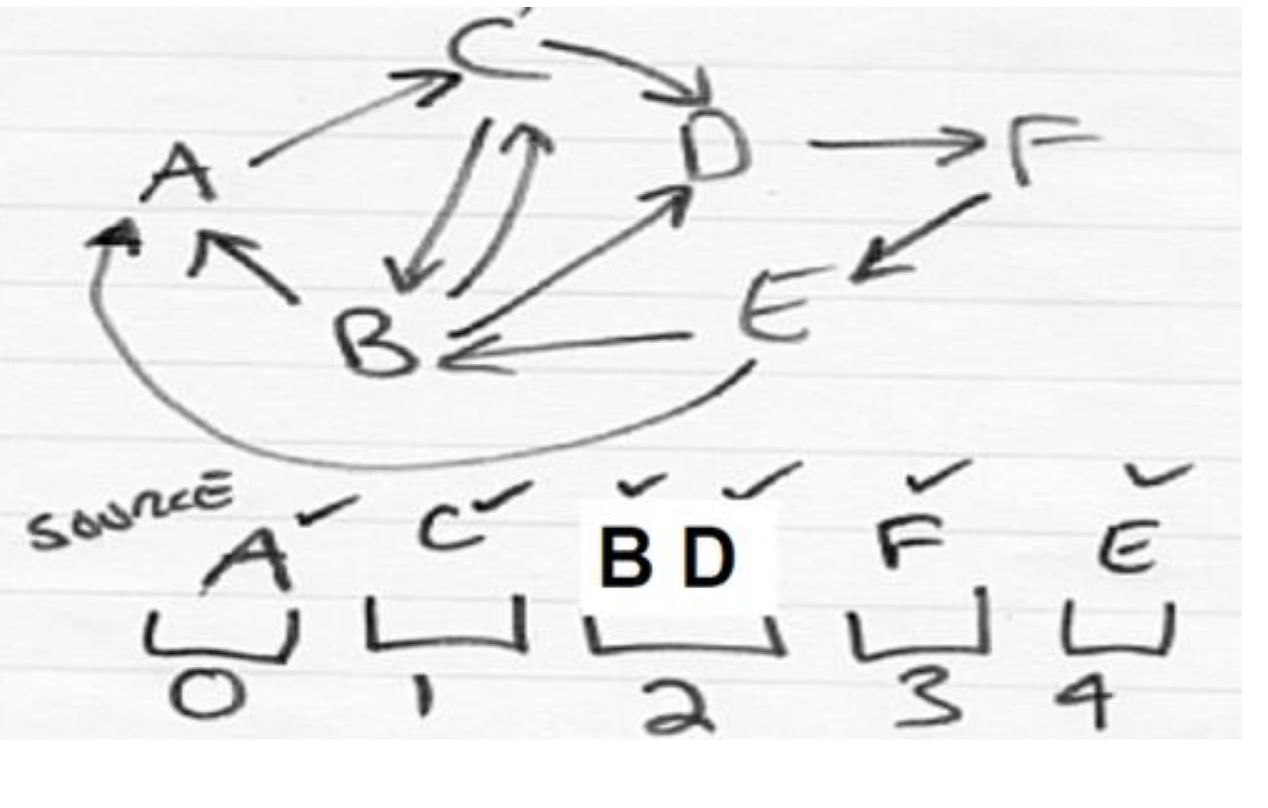
Breadth First Search

Visit vertices one edge from a given source, two edges from source, etc.

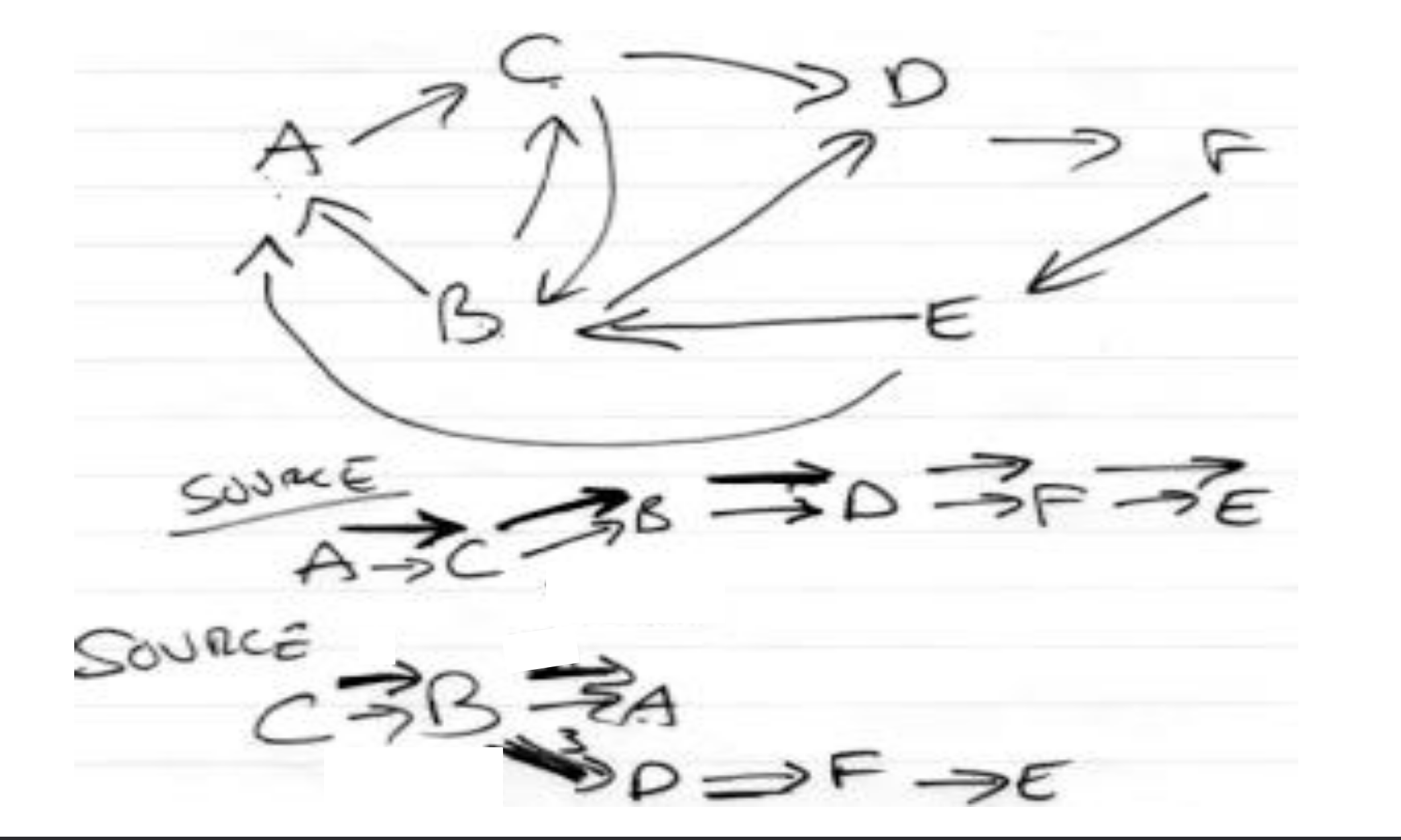
Depth First Search

As we visit a vertex we try to move to a new adjacent vertex that hasn’t yet been visited, until nowhere else to go, then backtrack.

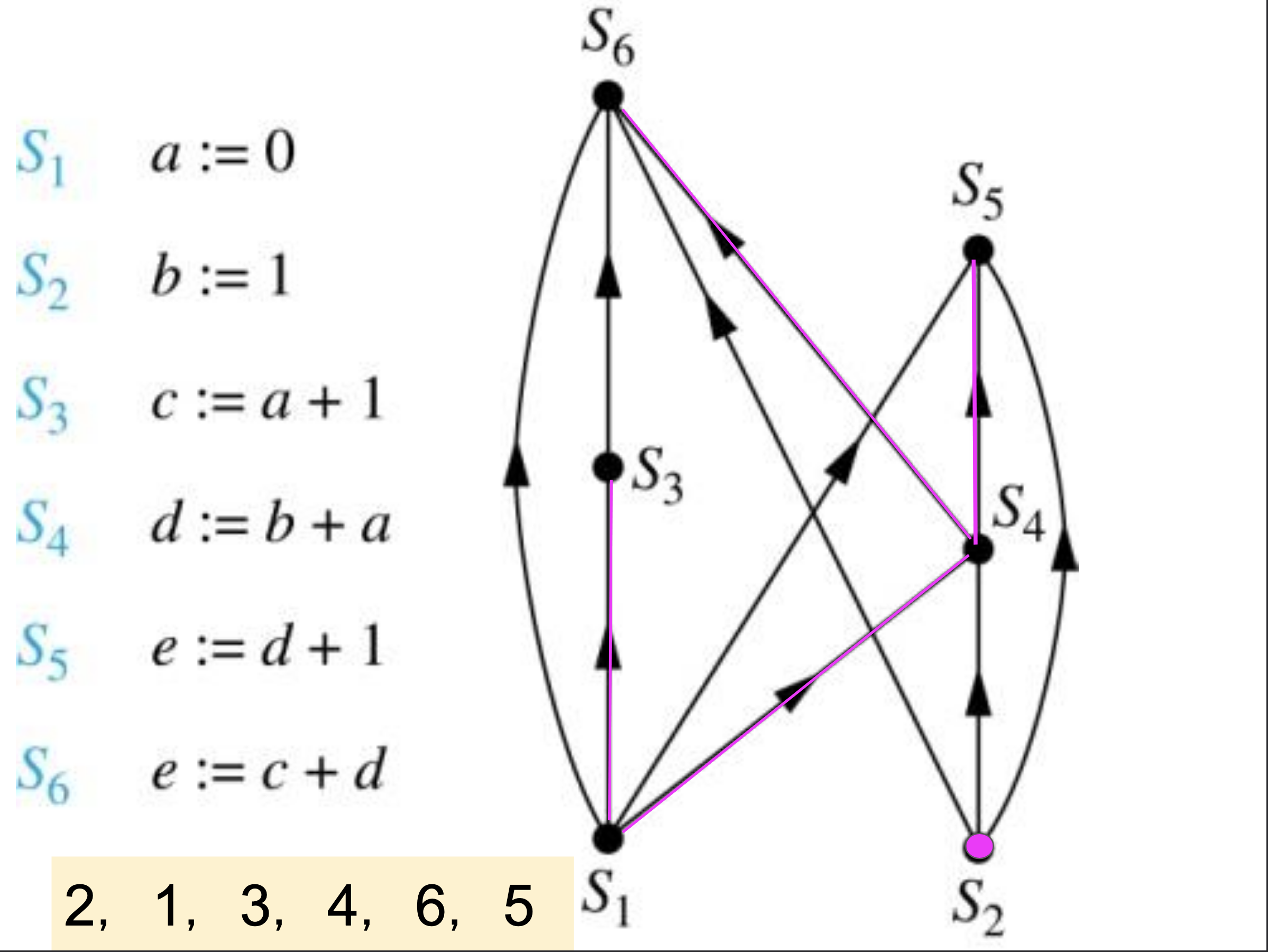
Topological Sort

A linear ordering of all its vertices such that if G contains an edge (u, v), then u appears before v in the ordering.

Tree

A connected undirected graph with no simple circuits.

Rooted Tree

A tree in which one vertex has been designated as the root and every edge is directed away from the root.

Forest

A forest is a graph that has no simple circuit, but is not connected. Each of the connected components in a forest is a tree.

Ordered Rooted Tree

Rooted tree where the children of each internal vertex are ordered.

Binary Tree

Rooted tree where each internal vertex has at most two children.

m-ary Tree

A rooted tree is called an m-ary tree if every internal vertex has no more than m children. The tree is called a full m-ary tree if every internal vertex has exactly m children.

Combination

An unordered arrangement of a set of distinct objects.

Graph Coloring

An assignment of colors to the vertices of a graph such that no two adjacent vertices share the same color.