MCAT Physics and Math - Fluids

228

Fluids

characterized by their ability to flow and conform to the shapes of their containers; liquids and gases

Solids

do not flow and are rigid enough to retain a shape independent of their containers

shear (tangential) forces

the component of stress coplanar with a material cross section, only solids can withstand

perpendicular forces

fluids and solids

ex. falling into water

density

ratio of their mass to their volume; scalar

ρ = m/V

where ρ (rho) represents density, m is mass, and V is volume

units: kg/m³, g/mL, g/cm³

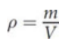
weight from density

multiplying the substance’s density by its volume and the acceleration due to gravity

F_g = ρVg

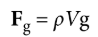
specific gravity

the density of a fluid compared to that of pure water at 1 atm and 4°C; can be used as a tool for determining if an object will sink or float in water

SG = ρ/1 g/cm³

density of pure water at 1 atm and 4°C

exactly 1 g/cm³

Pressure

ratio of the force per unit area; scalar; is the same at all points along the walls of the container and within the space of the container itself so applies in all directions at any point

P = F/A

where P is pressure, F is the magnitude of the normal force vector, and A is the area

measured in pascals (Pa = N/m²), mmHg, torr, atmosphere (atm)

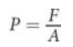
presure unit equivalence

1.013 × 10⁵ Pa = 760 mmHg ≡ 760 torr = 1 atm

Atmospheric pressure

changes with altitude; increases at lower altitudes; impacts a number of processes, including hemoglobin’s affinity for oxygen and the boiling of liquids

Absolute (hydrostatic) pressure

total pressure that is exerted on an object that is submerged in a fluid

P = P₀ + ρgz

where P is the absolute pressure, P₀ is the incident or ambient pressure, ρ is the density of the fluid, g is acceleration due to gravity, and z is the depth of the object

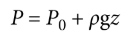
incident or ambient pressure (P₀)

the pressure at the surface, does not always stand for atmospheric pressure; often equal to 1 atm

ex. pressure cookers increase atosmpheric pressure to raise water’s boiling point, to reduce cooking time and prevent loss of moisture

gauge pressure

the difference between the absolute pressure inside the tire and the atmospheric pressure outside the tire

P_gauge = P – P_atm = (P₀ + ρgz) – P_atm

Hydrostatics

the study of fluids at rest and the forces and pressures associated with standing fluids

Pascal’s principle

fluids that are incompressible (volumes that cannot be reduced by any significant degree through application of pressure), a change in pressure will be transmitted undiminished to every portion of the fluid and to the walls of the containing vessel

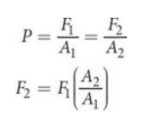
hydraulic systems

systems take advantage of the near-incompressibility of liquids to generate mechanical advantage

ex. car brakes, bull dozers, cranes, lifts

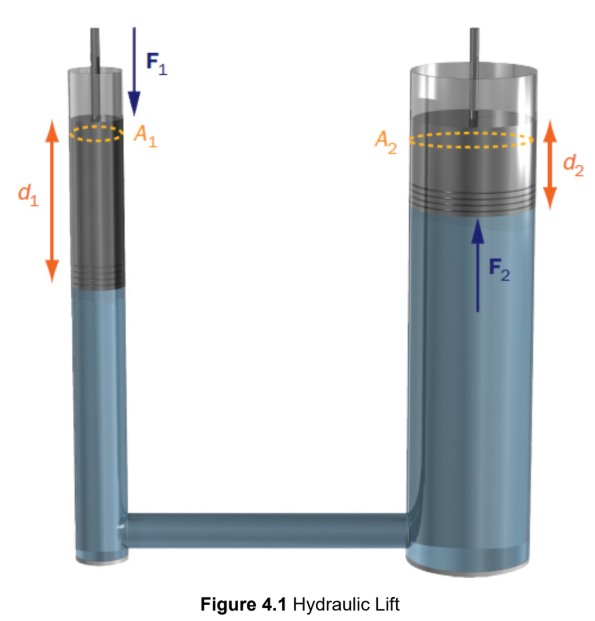
Pascal’s and distance moved

the volume displaced by piston 1 is equal to the volume dispkaced at piston 2

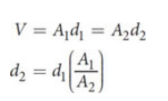
work and Pascal’s principle

derived from W = PΔV

Archimedes’ principle

a body wholly or partially immersed in a fluid will be buoyed upwards by a force equal to the weight of the fluid that it displaces.

F_buoy = ρ_fluidV_{fluid displaced}g = ρ_fluidV_submergedg

buoyancy/bouyant force/upthrust

net upward force exerted by a fluid that opposes the weight of a partially or fully immersed object; the force of the liquid trying to return to the space from which it was displaced, thus trying to push the object up and out of the water

F_buoy = ρ_fluidV_{fluid displaced}g = ρ_fluidV_submergedg

average density of object > density of fluid = no buoyant force = submerged fully

average density of object < density of fluid = buoyant force = floats

Surface tension

special physical property of liquids at the interface between a liquid and a gas that causes the liquid to form a thin but strong layer like a “skin” at the liquid’s surface; results from cohesion, molecules on surface have strong attractive forces from the molecules below them, which pulls the surface of the liquid toward the center.

cohesion

the attractive force that a molecule of liquid feels toward other molecules of the same liquid

ex. droplets of water

adhesion

the attractive force that a molecule of the liquid feels toward the molecules of some other substance

ex. car windshield on rainy day

meniscus

curved surface in which the liquid “crawls” up the side of the container a ; small amount; form when the adhesive forces are greater than the cohesive forces; measure from trough of meniscus

ex. water

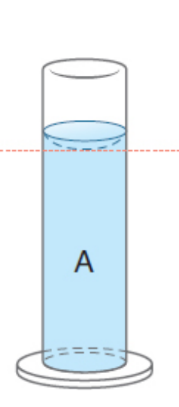
backwards (convex) meniscus

the liquid level higher in the middle than at the edges, occurs when the cohesive forces are greater than the adhesive forces; measure from peak of meniscus

ex. mercury

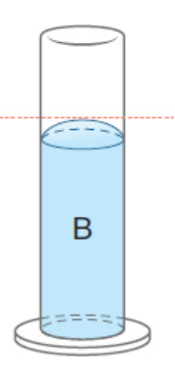
fluid dynamics

study of fluids in motion

viscosity (η)

the resistance of a fluid to flow; more viscous fluids will “lose” more energy while flowing; mostly negligible

unit is pascal-second (Pa*s)

viscous drag

nonconservative force that is analogous to air resistance, caused by increased viscosity

inviscid

no viscosity, only ideal fluids

Laminar flow

smooth and orderly flow, modeled as layers of fluid that flow parallel to each other; the layer closest to the wall of a pipe flows more slowly than the more interior layers of fluid

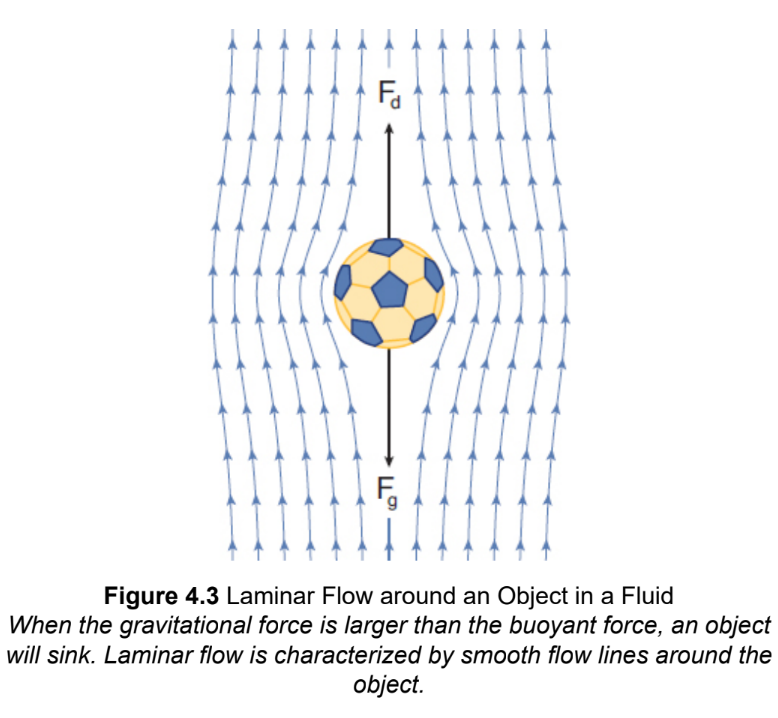
Poiseuille’s law

calculate the rate of flow with laminar flow through a pipe or confined space

where Q is the flow rate (volume flowing per time), r is the radius of the tube, ΔP is the pressure gradient, η (eta) is the viscosity of the fluid, and L is the length of the pipe.

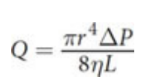
Turbulent flow

rough and disorderly flow, cauing eddies

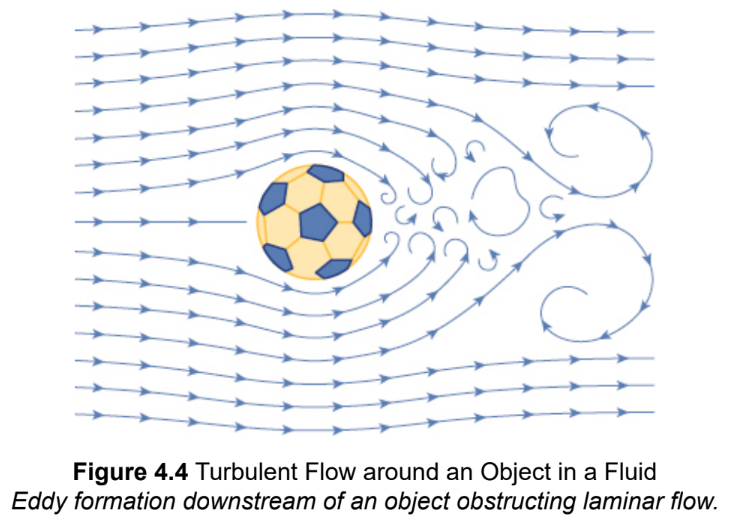
eddies

swirls of fluid of varying sizes occurring typically on the downstream side of an obstacle

critical speed

turbulence can arise when the speed of the fluid exceeds this threshold; depends on the physical properties of the fluid, such as its viscosity and the diameter of the tube

where vc is the critical speed, NR is the Reynolds number, η is the viscosity of the fluid, and ρ is the density of the fluid.

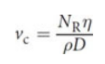
boundary layer

the thin layer of fluid adjacent to the wall, where laminar flow occurs even past critical speed; the flow speed immediately at the wall is zero and increases uniformly throughout the layer

Reynolds number

dimensionless constant depends on factors such as the size, shape, and surface roughness of any objects within the fluid

streamlines.

indicate the pathways followed by tiny fluid elements/particles as they move; velocity vector of a fluid particle will always be tangential to the streamline

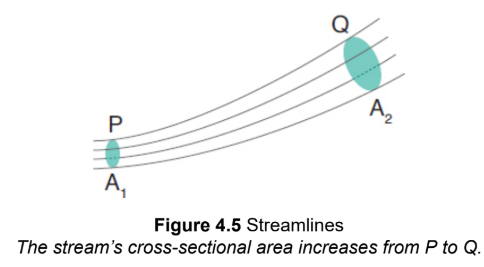
flow rate

the volume per unit time, constant for a closed system and is independent of changes in cross-sectional area; the product of linear speed and cross-sectional area

Linear speed

a measure of the linear displacement of fluid particles in a given amount of time;

continuity equation

fluids will flow more quickly through narrow passages and more slowly through wider ones

Q = v1A1 = v2A2

where Q is the flow rate, v1 and v2 are the linear speeds of the fluid at points 1 and 2, respectively, and A1 and A2 are the cross-sectional areas at these points.

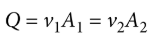
Bernoulli’s equation

where P is the absolute pressure of the fluid, ρ is the density of the fluid, v is the linear speed, g is acceleration due to gravity, and h is the height of the fluid above some datum

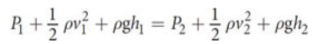
dynamic pressure

pressure associated with the movement of a fluid, kinetic energy divided by volume

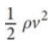
energy density

ratio of energy per cubic meter

ex. pressure

static pressure

absolute pressure although h is used here to imply height above a certain point, whereas z was used earlier to imply depth below a certain point

pitot tubes

specialized measurement devices that determine the speed of fluid flow by determining the difference between the static and dynamic pressure of the fluid at given points along a tube

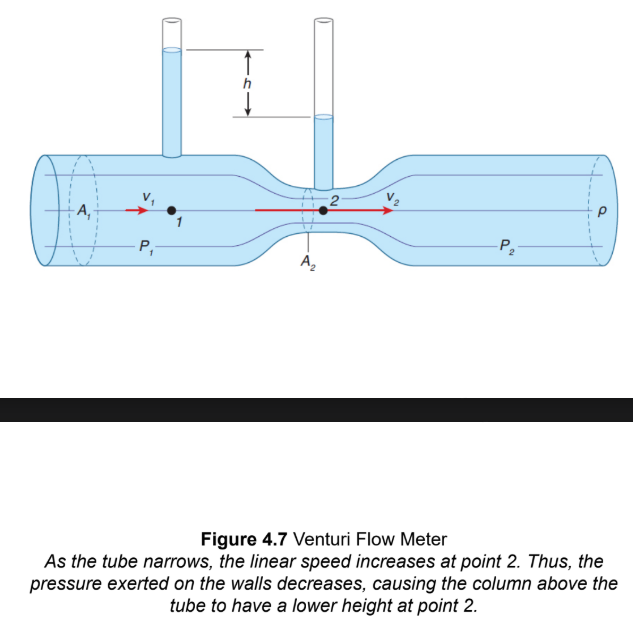
Venturi flow meter/Venturi effect

start by noting that the average height of the tube itself remains constant. therefore, the ρgh term remains constant at points 1 and 2. Note that the h shown in Figure 4.7 is the difference in height between the two columns at points 1 and 2, not h from Bernoulli’s equation, which corresponds to the average height of the tube above a datum. As the cross-sectional area decreases from point 1 to point 2, the linear speed must increase according to the continuity equation. then, as the dynamic pressure increases, the absolute pressure must decrease at point 2. With a lower absolute pressure, the column of fluid sticking up from the Venturi tube will be lower at point 2.

closed loop

a processing system in which effluents are recycled, that is, treated and returned for reuse

pulse

the regular throbbing of the arteries, caused by the successive contractions of the heart, especially as may be felt at an artery, as at the wrist

circulatory system

closed lop w/ nonconstant flow rate

• valves

• gravity

• elasticity of vessels

• heart mechanics

• felt as pulse

loss of volume - difference btwn osmotic/oncotic and hydrostatic pressures

• returned by lymphatic system

volume leaving heart = volume entering heart

more resistance further from heart BUT vessels are all in parallel so total resitance decreases

return flow - mechanical squeezing of skeltal muscles → increases limb pressure + expansion of heart → decreases pressure

pressure gradients created in the thorax by inhalation and exhalation also motivate blood flow

Venous circulation holds approximately three times as much blood as arterial circulation.

Heart murmurs, which result from structural defects of the heart, are heard because of turbulent blood flow.

Respiratory system

mediated by changes in pressure

inspiration - negative pressure gradient that moves air into the lungs

expiration - this gradient reverses

when air reaches the alveoli, it has essentially no speed