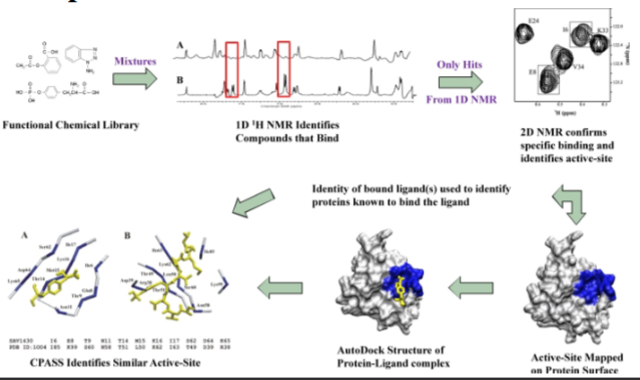
Modern Ch. 19 (Nuclear Magnetic Resonance Spectroscopy)

NMR Spectroscopy in a Nutshell

Nuclear magnetic resonance (NMR) spectroscopy is based on the measurement of the absorption of EM radiation in the radio- frequency range of roughly 4 to 900 MHz.
Nuclei of atoms are involved in the absorption process.
To cause nuclei to develop the energy states required for absorption to occur, the analyte must be placed in a magnetic field.
Two types of NMR, continuous-wave and Fourier transform
- 1970's switch from CW-NMR to FT-NMR and nearly all NMR
instruments produced today are FT

Quantum Description of NRM: Spin

To account for the properties of certain nuclei, we must assume that the nuclei rotate about an axis and thus have the property of "spin".
Nuclei with this property of "spin" have an angular momentum (p).
Analogous to a magnetic field produced when electricity flows through a coil of wire, a spinning, charged nucleus creates a magnetic field with a magnetic moment (μ), which is oriented along the axis of spin and is proportional to the angular momentum:
μ = γp
where the proportionally constant is referred to as the magnetogyric, (or gyromagnetic ratio) (γ).
NOTE: The magnetogyric ratio (γ) is a factor in the relationship between the frequency of the absorbed energy and the magnetic field strength

Quantum Description of NRM: Nuclei of Interest

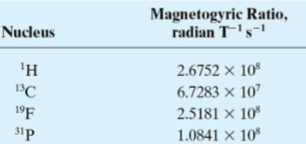
¹H, ¹³C, ¹⁹F, and ³¹P nuclei useful for organic chemistry and biochemistry and thus will be focus of our discussion.

magnetogyric ratio (γ)
The "spin" for these nuclei is 1/2 and thus have two spin states corresponding to +1/2 and -1/2.
The relationship between nuclear spin and magnetic moments leads to a set of observable magnetic quantum states (m), +1/2 and -1/2.
Note: heavier nuclei can have spin numbers that range from 0 (no net spin component) to 9/2.

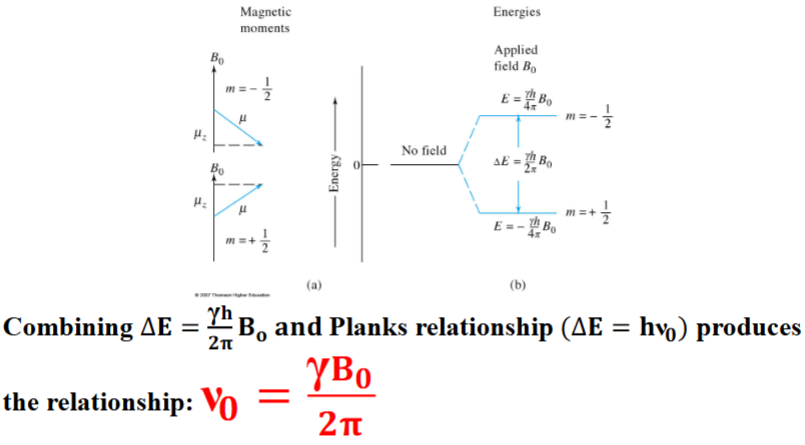
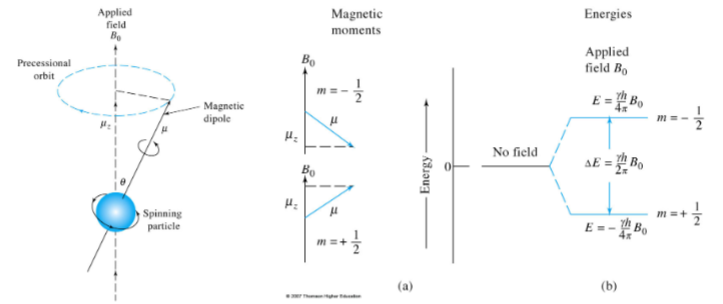
Quantum Description of NMR Spectroscopy

When a nucleus with a spin quantum number of 1/2 is brought into an external magnetic field (B0), its magnetic moment (μ) becomes oriented in one of two directions, with respect to the magnetic field, depending on its magnetic quantum state. The absorption/emission of the frequency (ν0) can be related to the magnetogyric ratio.

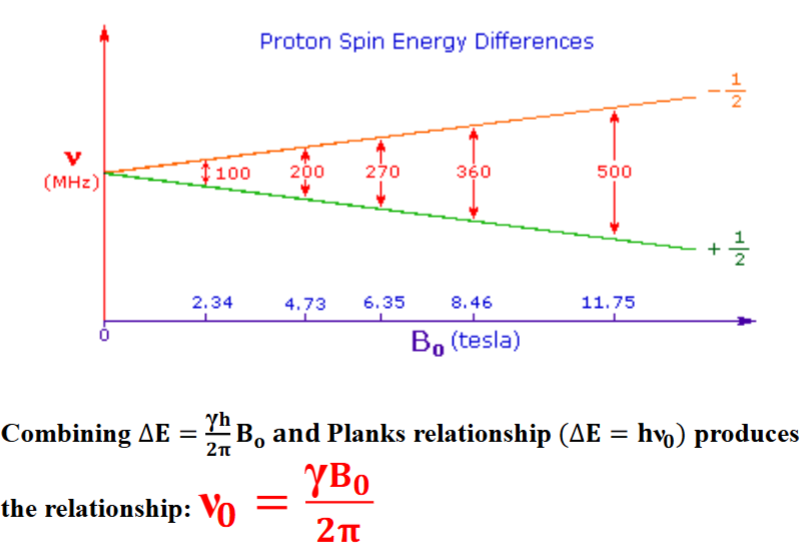
Proton Spin Energy Differences

Classical Description of NMR Spectroscopy

A classical picture of the behavior of a charged particle in a magnetic field helps rationalize the measurement of the absorption process involved in NMR.
We can consider a spinning particle (nuclei) in a applied magnetic field (B0 ) analogous to a gyroscope when it is displaced from the vertical position by application of a lateral force

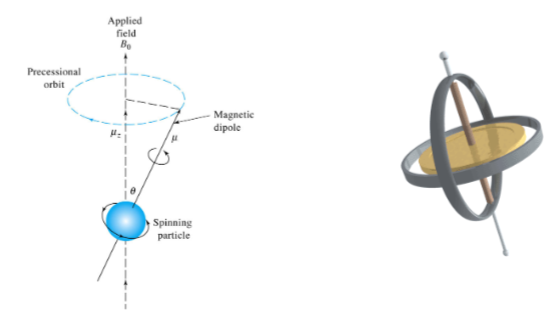
Classical Description of NMR Spectroscopy

The angular velocity of this motion (ω 0) is related to the applied magnetic field via the magnetogyric, (or gyromagnetic ratio) (γ): ω 0 = γB₀
The angular velocity can be converted to the frequency of precession (ν0) known as the Larmor frequency by diving by 2 π: ν₀ = γ 𝑩₀/𝟐𝝅
Note this is the identical equation as the quantum mechanical description of NMR.

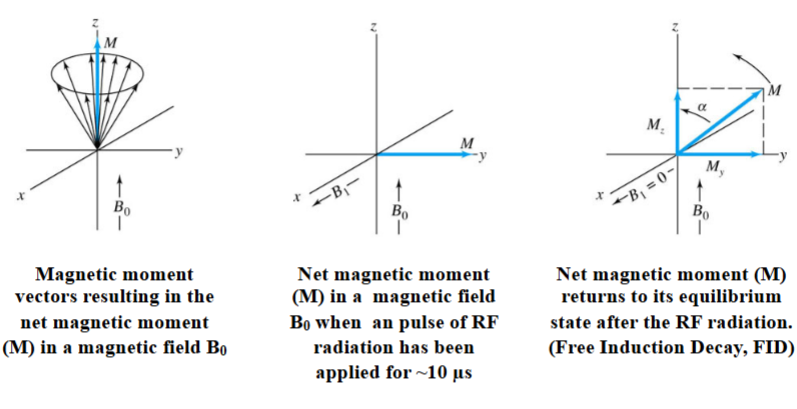
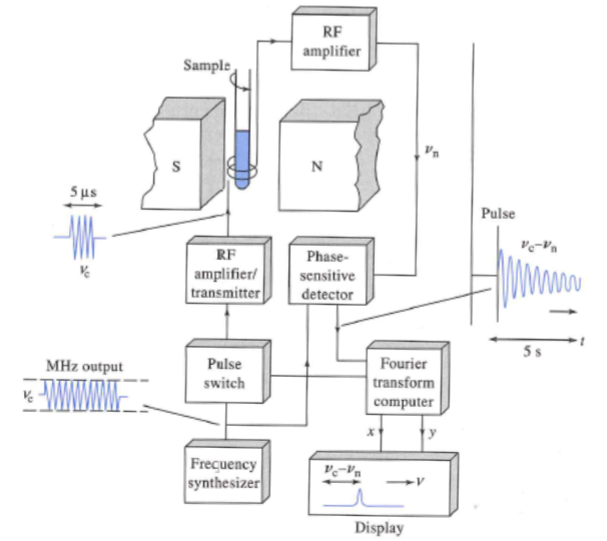
Fourier Transform NMR

Nuclei in a strong magnetic field are subjected periodically to very brief pulses of
intense RF radiation.
Figure A shows the waveform including the pulse train, pulse width, and timer intervals between pulses.
Figure B shows an expanded view of one of the pulses illustrating that each pulse is an actual packet of RF radiation.
Pulses are typically less than 10 μs and the frequency is on the order of 10 2 to 103
MHz. The interval between the pulses (T) is typical a several seconds.
During T, a time-domain RF signal, called the free-induction decay (FID) signal, is emitted by the nuclei as they relax. This is due to two mechanisms: spin-lattice and spin-spin lattice interactions. This signal is collected by a RF coil (typically the same used to make the pulse) and stored for data processing (e.g. FT).

Pulsed Excitation via RF Radiation

With each RF pulse, the magnetic moment of the nuclei (M) experiences torque that tips it off the z axis.

Relaxation Processes in NMR Spectroscopy

Spin-Lattice Relaxation (T₁) and Spin-Spin Relaxation (T₂)

Spin-Lattice Relaxation (T₁)

Lattice refers to the collection of atom that makeup of the sample. Vibrational and rotational motion of these nuclei creates a complex field around each magnetic nucleus and contains a continuum of magnetic components. These components interact and convert nuclei from a higher to a lower state. It is a first-order exponential decay.

Spin-Spin Relaxation (T₂)

Various effects that diminish relaxation times and broaden NMR lines. Neighboring nuclei of the same kind have identical precession rates but are in different magnetic fields of each can interact to cause an interchange of states. Net-effect s a decrease in the lifetime

Free-Induction Decay (1)

¹³C FID signal and FT of the signal of dioxane when the pulse frequency is identical to the Larmor frequency.

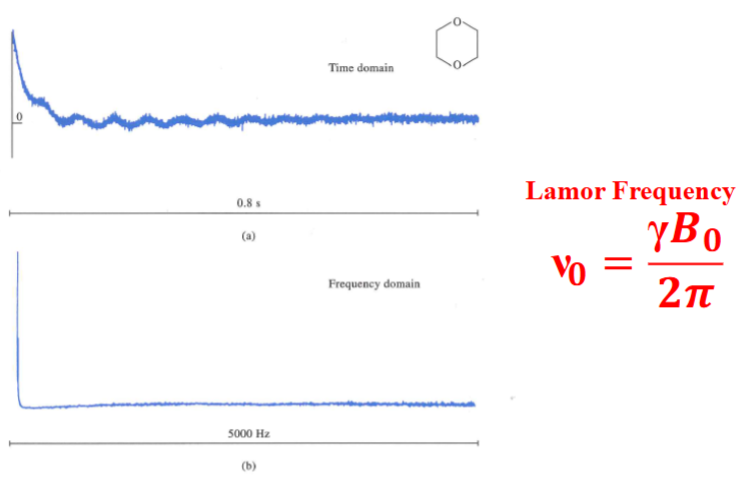
Free-Induction Decay (2)

¹³C FID signal and FT of the signal of dioxane when the pulse frequency is offset to the Larmor frequency by 50 Hz.

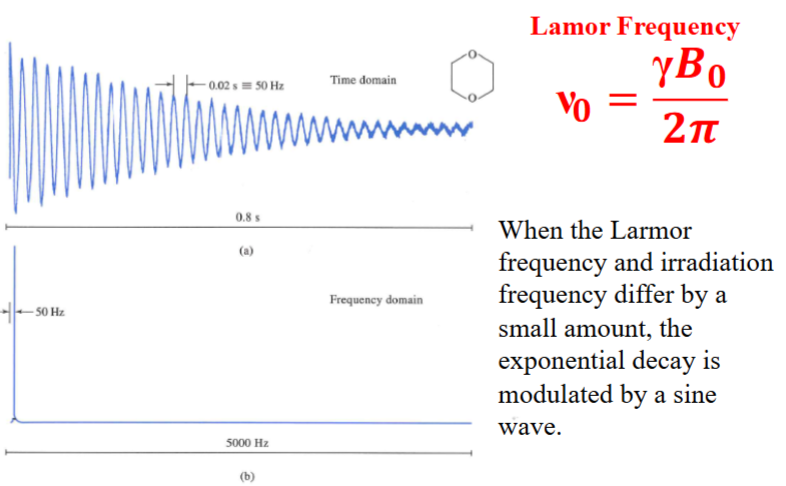
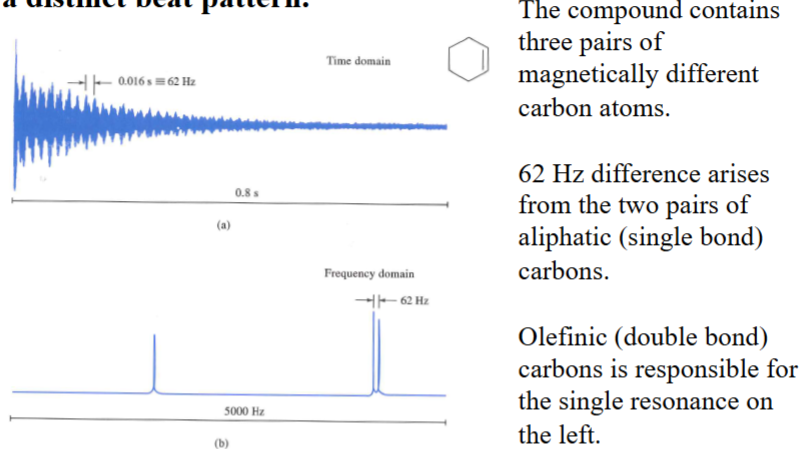
Free-Induction Decay (3)

¹³C FID signal and FT of the signal of cyclohexne. When magnetically different nuclei are present, the FID develops a distinct beat pattern.

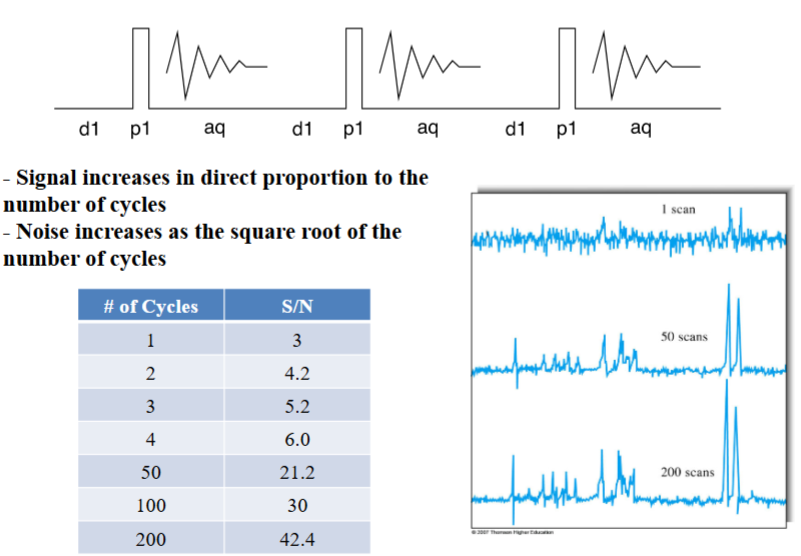
Putting Everything Together: Simple 1D Acquisition

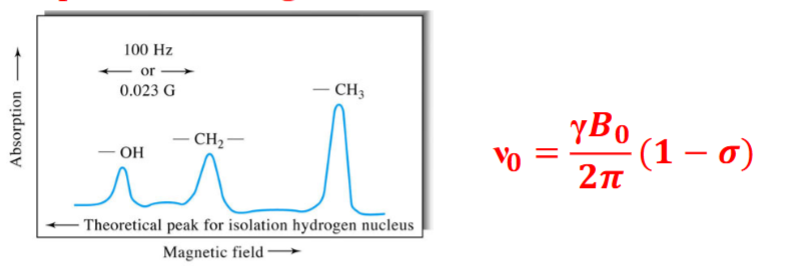
Origins of the Chemical Shift

Chemical shifts are cause by small magnetic fields generated by the electrons as they circulate around nuclei. Typically, nuclei are exposed to an effective field that is smaller than the external field. This is directly proportional to the applied external field.

𝐁₀ = 𝐁_appl − 𝛔𝐁_appl = 𝐁_appl (𝟏 − 𝛔)

B₀ is the magnitude of the resultant field, which determines the resonance behavior of the nucleus
B_appl is the magnitude of the applied filed and
σ is the shielding constant determined by the electron density and spatial distribution around the nucleus

Origins of the Chemical Shift

The electron density depends on the structure of the compound containing the nucleus.

Example: Ethanol
The screening constant in a methyl is larger than the corresponding constant for a methylene protons, and it is even smaller for the proton in an -OH group.
Note either the B appl or the excitation oscillator frequency must be held constant while the other component is increased to bring about the resonance condition. The shielding (σ) differs for protons for various functional groups

Abscissa Scales for NMR (1)

The absolute magnetic field strength with the accuracy required for high resolution NMR is impossible. But, the magnitude of a change in the field strength is possible to within a tenth of milligauss or better.
Therefore, report the position of resonances relative to the resonance for an internal standard. It depends on the nucleus being studied and the solvent system.
For example, tetramethylsilane (TMS) is used for proton NMR in organic solvents. It is inert and readily soluble in organic solvents.

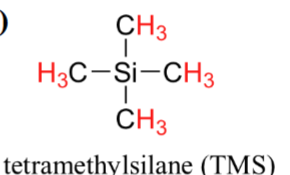
Abscissa Scales for NMR (2)

- We use the chemical shift parameter (δ) to express the chemical shift relative to the internal standard where: δ = (σ_r - σ_s) × 10⁶
- σr shielding constant of analyte sample and σs refers to the shielding constant of the internal standard.
- An advantage of this strategy is that for a given resonance, δ is the same regardless of whether a 200- or a 800-MHz instrument is used.
- Most proton resonances lie in the δ range of 1 to 13.
- The chemical shift is enhanced with the higher frequency instrument.

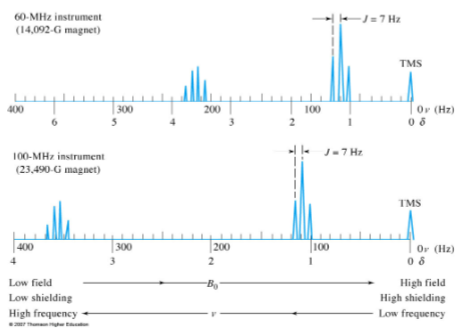
Abscissa Scales for NMR (3)

- Historically the data were plotted with the field increasing from left to right. Thus, the internal standard (e.g.: TMS) will appear on the far right hand side of the plot.
- Zero corresponds to the internal standard (e.g.: TMS) peak.
- Other nuclei have different ppm ranges: ¹³C = 0 to 220 ppm, ¹⁸F = 0 to 800 ppm, ³¹P = 0 to 300ppm

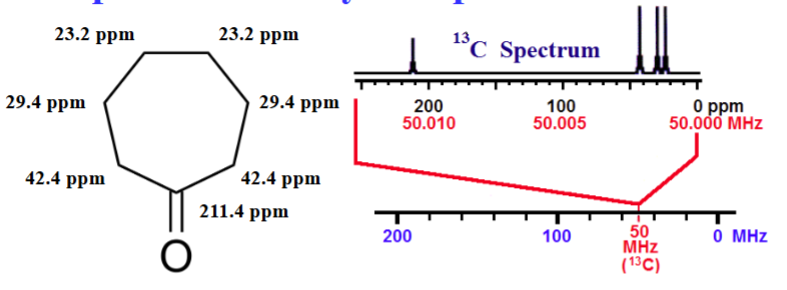
¹³C Spectrum for Cyclohepatanone

Resonant frequency for a particular nucleus at a specific position a molecules is equal to a fundamental frequency of that isotope (50.00 MHz for ¹³C) multiplied by a factor for the chemical shift.
Resonant Frequency = ν 0 (1 + (δ × 10^-6 ))
For the ¹³C nucleus @ the C4 potions of cycloheptanone (δ = 23.2 ppm) resonates at 50.00 MHz (1+(23.2 × 10^-6 )) = 50.001160 MHz

NMR Hardware: ~$1000/MHz

NMR Components: Magnets

permanent, conventional, superconducting magnets

Permanent magnets

are seldom used because of little to no control due to low field strengths, temperature sensitivity, and drift

Conventional magnets

are seldom used for same reasons as permanent magnets.

Superconducting magnets

are used in most modern instruments and can attain magnetic fields as large as 23 T, which corresponds to a proton frequency of 1 GHz. Wrapped niobium-tin/niobium-titanium wire bathed in liquid helium Dewar flask surrounded by liquid nitrogen. Liquid nitrogen must be filled once a week and liquid helium every few months. Advantages of superconducting magnets: high field strengths, high stability, low operating cost, simplicity, small size compared to permanent and electromagnet.

NMR Components: Locking the Magnetic Field

A reference nucleus is continuously irradiated and monitored at a frequency corresponding to its resonance maximum at the radiated field strengths of the magnet.
Changes in the intensity of the reference signal control a feedback circuit to correct for drift.
Typically, the reference signal is provided by the deuterium in the solvent with a second transmitter coil tuned to the frequency deuterium.
Most common instruments can run for 1-20 min without being locked.

NMR Components: Shimming

pairs of wire loops, which carry currents, to adjust and correct for magnetic field inhomogeneities.
Computer controlled and done for each sample

NMR Components: Sample Spinning

the sample along its longitudinal axis counteracts field inhomogeneities.
By spinning the sample at 20 to 50 revolutions per minute to attain an average reading.
A minor disadvantage of spinning is that magnetic field is modulated at the spinning frequency, which may lead to side bands

NMR Components: Sample Probe

- Holds the sample in a fixed position
- Contains an air turbine for spinning
- Houses coils for excitation and detection
- Houses coils for locking and decoupling experiments
- Variable temperature capabilities
Typical size of NMR sample cell: 5 mm outside diameter tube containing 500-650 μL of liquid

NMR Sample Handling

- Typically 2% to 15% solution of the sample is used, but pure liquid samples can also be examined if there viscosities are sufficiently low.
- Solvent must have no resonances of their own in the spectral region of interest. Usually, NMR solvents are deuterated to provide the field-frequency lock signal. Most common solvents include deuterated chloroform (CDCl3 ), CD 3 OD, acetone-d 6 , and DMSO-d 6 .
- NMR tubes must be cleaned and dried prior to use. Chromic acid- sulfuric acid should not be used as chromium ions can absorb to the walls and broaden proton NMR spectra

Applications of Proton (¹H) NMR

Identification of Compounds, Quantitative Analysis

Identification of Compounds

- ID components by combining NMR spectra with Mass spectrometry and FTIR.
- Identify functional groups such as hydroxyl groups, aldehydes, olefins, etc.

Quantitative Analysis

- Amount of 1 H is directly proportional to peak areas and number of nuclei responsible for the peak.
- Does not require pure samples for calibration. Instead, one needs to know signal area per proton. This quantity can be obtained from a known concentration of an internal standard.
- Cost, potential of overlapping resonances, sensitivity, and convenience, limits the instrument for quantitative work

Applications of ¹³C NMR

Widespread use began in the 1970's although it was first studied in the 1950's.
Because of sensitivity:
1) low natural abundance 1.1% of all carbon
2) Small magnetogyric ratio (0.25)
In other words, 13 C NMR is ~6000 times less sensitive than 1 H NMR!
Advantages of 13 C NMR compared to 1 H NMR
1) Backbone rather than periphery of molecules
2) Chemical shifts are over a large range (200 ppm 13 C NMR versus 15 ppm for ¹H NMR)
3) Homonuclear coupling not observed because 13 C is very rare (1.1% of all carbon).
4) Methods exist to decouple protons and carbon atoms

Applications of NMR with other Nuclei

Nuclei must have a magnetic moment
- examples include ³¹P, ¹⁵N, ¹⁹F, ²D, ¹¹B, ²³N, etc.
Useful for biomolecules/proteins Inorganic species