Chapter 7: Design of a Study: Sampling, Surveys, and Experiments
In this chapter, we study techniques for gathering data so that we have reasonable confidence that they are representative of our population of interest.
Census
- A procedure by which every member of a population is selected for study.
- Doing a census when the population of interest is quite large, is often impractical, too time-consuming, or too expensive.
- The goal of sampling is to produce a representative sample, one that has the essential characteristics of the population being studied and is free of any type of bias.
Probability Sample
- A list of all members of the population from which we can draw a sample is called a sampling frame.
- A probability sample is one in which each member of the population has a known probability of being in the sample.
- Probability samples use some sort of random mechanism to choose the members of the sample.
Types of probability samples:
1.Random Sampling Techniques
Random Sample: Each member of the population is equally likely to be included.
Simple Random Sample (SRS): A sample of a given size is chosen in such a way that every possible sample of that size is equally likely to be chosen.
Systematic Sample: The first member of the sample is chosen according to some random procedure, and then the rest are chosen according to some well-defined pattern.
[[A systematic sample is random because of the random start, but not a simple random sample because not every sample of size n is equally likely.[[
Stratified Random Sample: The population is first divided into distinct homogeneous subgroups called strata and then a random sample is chosen from each subgroup. For example, you might divide the population of voters into groups by political party and then select an SRS of 250 from each group.
Cluster Sample: The population is first divided into sections or “clusters.” Then we randomly select one or more clusters and include all the members of the selected cluster(s) in the sample.
2.Non-Random Sampling Techniques
- Self-Selected Sample or Voluntary Response Sample: People choose whether or not to participate in the survey. A radio call-in show is a typical voluntary response sample.
- Convenience Sampling: The pollster obtains the sample any way he can, usually with the ease of obtaining the sample in mind. For example, handing out questionnaires to every member of a given class at school.
- Quota Sampling: The pollster attempts to generate a representative sample by choosing sample members based on matching individual characteristics to known characteristics of the population. This is similar to a stratified random sample, only the process is non random.
Sampling Bias
- Undercoverage: This happens when some part of the population being sampled is somehow excluded. This can happen when the sampling frame isn’t the same as the target population.
Example:
A pollster conducts a telephone survey to gather opinions of the general population about welfare. Persons too poor to be able to afford a telephone are certainly interested in this issue but will be systematically excluded from the sample. The resulting sample will be biased because of the exclusion of this group.
- Voluntary Response bias: This occurs with self-selected samples. Persons who feel most strongly about an issue are most likely to respond.
Example:
You decide to find out how your neighbors feel about the neighbor who seems to be running a car repair shop on his front lawn. You place a questionnaire in every mailbox within sight of the offending home and ask the people to fill it out and return it to you. About 1/2 of the neighbors return the survey, and 95% of those who do say that they find the situation intolerable. We have no way of knowing the feelings of the 50% of those who didn’t return the survey—they may be perfectly happy with the “bad” neighbor. Those who have the strongest opinions are those most likely to return your survey—and they may not represent the opinions of all. Most likely they do not.
- Nonresponse bias: The possible biases of those who choose not to respond, is a related issue.
- Wording bias: This occurs when the wording of the question itself influences the response in a systematic way.
Example:
Compare the probable responses to the following ways of phrasing a question.
(i) “Do you support using taxpayers’ money for sculpture in public spaces?”
(ii) “Do you support beautification of public spaces with sculpture from local
artists?”
It’s likely that (i) is designed to show that people are against public art and that (ii) is designed to show that people are in favor of public art. The authors of both questions would probably argue that both responses reflect society’s attitudes toward public art.
- Response bias: The respondent may not give truthful responses to a question, the respondent may fail to understand the question, the respondent desires to please the interviewer, the ordering of the question may influence the response, etc.
Example:
What form of bias do you suspect in the following situation? You are a school principal and want to know students’ level of satisfaction with the counseling services at your school. You direct one of the school counselors to ask her next 25 counselees how favorably they view the counseling services at the school.
Solution:
A number of things would be wrong with the data you get from such a survey.
- First, the sample is nonrandom—it is a sample of convenience obtained by selecting 25 consecutive counselees. They may or may not be representative of students who use the counseling service.
- Second, you are asking people who are seeing their counselor about their opinion of counseling. You will probably get a more favorable view of the counseling services than you would if you surveyed the general population of the school.
- Also, because the counselor is administering the questionnaire, the respondents would have a tendency to want to please the interviewer. This would be a response bias.
- The sample certainly suffers from Undercoverage—only a small subset of the general population is actually being interviewed. What do those not being interviewed think of the counseling?
Experiments and Observational Studies
Statistical Significance:
- One of the desirable outcomes of a study is to help us determine cause and effect.
- We say that a difference between what we would expect to find if there were no treatment and what we actually found is statistically significant if the difference is too large to attribute to chance.
- An experiment is a study in which the researcher imposes some sort of treatment on the experimental units.
- An observational study , on the other hand, simply observes and records behavior but does not attempt to impose a treatment in order to manipulate the response.
- There are two classes of observational studies: retrospective and prospective .
Retrospective Studies: These studies examine data for a sample of individuals. Sample surveys are retrospective studies.
Prospective Studies: These studies select a sample of individuals and follow their behavior as time goes on. Sometimes over many years.
Confounding Variable
[[A confounding variable is one that has an effect on the outcomes of the study but whose effects cannot be separated from those of the treatment variable.[[
Example:
A study is conducted to see if Yummy Kibble dog food results in shinier coats on golden retrievers. It’s possible that the dogs with shinier coats have them because they have owners who are more conscientious in terms of grooming their pets.
Both the dog food and the conscientious owners could contribute to the shinier coats. ==The variables are confounded because their effects cannot be separated.==
3 Basic Principles of Experimental Design.
- Statistical control refers to a researcher holding constant variables not under study that might have an influence on the outcomes.
- Randomization is to equalize groups so that the effects of extraneous variables are equalized among groups. It involves the use of chance to assign subjects to treatment and control groups.
- Replication involves applying the treatment to enough subjects to reduce the effects of chance variation on the outcomes.
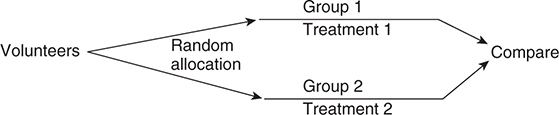
Completely Randomized Design
Involves three essential elements:
- Random allocation of subjects to treatment groups
- Administration of different treatments to each randomized group.
Some sort of comparison of the outcomes from the various groups.
Double-Blind Experiments
- A study is said to be double-blind when neither the subjects nor the evaluators know which group(s) is/are receiving each treatment or control.
- Reason: On the part of subjects, simply knowing that they are part of a study may affect the way they respond, on the part of the evaluators, knowing which group is receiving which treatment can influence the way in which they evaluate the outcomes.
Randomized Block Design
- Randomization as the main method to control for confounding variables.
- Randomized block design involves doing a completely randomized experiment within each block.
- A particular block design of interest is the matched-pairs design.
- One possible matched-pairs design involves before and after measurements on the same subjects. In this case, each subject becomes a block on which the experiment is conducted.
- Another type of matched pairs involves pairing the subjects in some way (matching on, say, height, race, age, etc.)
Click the link to go to the next chapter