Chapter 7

Axis

center point around which circular motion occurs

Rotation

circular motion around an internal axis

Revolution

circular motion around an external axis

Period, T

time it takes to make one complete oscillation; SI unit- s

Frequency, f

number of cycles made in a given time, usually a second; SI unit- Hz, 1/s, or s^-1

Angular Displacement, θ

angle through which an object rotates; positive is counter clockwise and negative is clockwise

Angular Displacement SI Unit

radian

Angular Displacement convert measurements of

360° degrees = 2π

Angular Displacement equation

s/r; arc length / radius

Angular Velocity, ω

rate of angular displacement

Angular Velocity Equation

ω = Δθ/t

Angular Velocity SI unit

rad/s

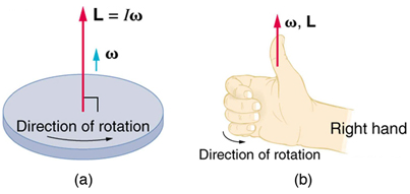
Angular Velocity Right Hand Rule

the direction in which the thumb of your right hand points when you curl your fingers in the direction of rotation

Does angular speed depend on radius?

No

Tangential Velocity, v_t

the speed and direction of an object moving in a circle; direction is always tangent to the circle; aka linear speed

Tangential Velocity Equations

v_t = rω

v_t = 2πr/T or = C/T

Does tangential speed depend on radius?

Yes

Tangential Velocity SI Unit

m/s

UCM

motion of an object travelling at a constant speed in a circular path with fixed radius; use circumference (C = 2πr   or C = πd)

Speed of an object in UCM equation

v_t = 2πr/T

How does an object accelerate if it’s moving at a constant speed?

For an object in UCM the magnitude of tangential velocity is constant but its direction is constantly changing (varying velocity) and therefore, accelerate even with constant speed (same magnitude of velocity)

Centripetal Acceleration, a_c

acceleration towards a circle’s center

Centripetal Acceleration Equations

a_c = v_t²/r 
a_c = rω²

Centripetal Force, F_c

force that causes centripetal acceleration. It isn’t a new force, just a force caused by something pulling inward, such as friction, weight, or tension

Centripetal Force Equation

F_c = m a_c

Un-banked curve

a curve that is not inclined above the horizontal, ex: level

What force holds an object in an unbanked curve?

friction causes the centripetal force

Un-banked curve equation to determine maximum speed

F_c = F_s → v_t = sqrt(u_sgr)

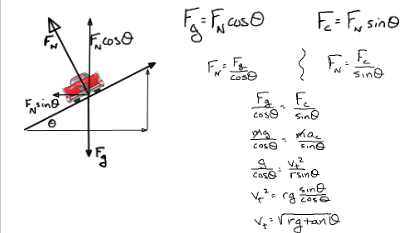
Banked Curves

incline; inclining the turn in the axial direction

What is the main reason an object stays on a banked curve?

reduces the reliance on friction when turning the corners

Banked Curve equation to determine maximum speed

F_g = F_Ncos(θ) & F_c = F_Nsinθ → v_t = sqrt(rgtanθ)

Angular Acceleration, α

when circular motion is nonuniform; rate of angular velocity changes

Angular Acceleration Equation

α = Δω/t

Angular Acceleration SI unit

rad/s²

Angular Acceleration Right Hand Rule

find angular velocity with right hand rule then extend thumb to point in direction of angular velocity then:

If the angular velocity points upward and is increasing, then the angular acceleration points in the same direction as angular velocity. If the angular velocity is decreasing, then the angular acceleration points in the opposite direction of the angular velocity. Likewise, if the angular velocity is pointing downward and is increasing, then the angular acceleration also points downward. On the other hand, if the angular velocity points downwards and is decreasing, then the angular acceleration points upward

Rotational Kinematic Equations

ω = ω_ο + αt

θ = ω t

θ = ω_ot + ½αt²

ω² = ω_o² + 2αθ

* only if acceleration is constant

Tangential Acceleration, a_t

if tangential speed changes, an acceleration is occurring.

Tangential Acceleration Equation

a_t = rα

Tangential Acceleration SI unit

m/s²

Total Acceleration, a

vector sum of centripetal and tangential acceleration

Total Acceleration equation

a² = a_c² + a_t²

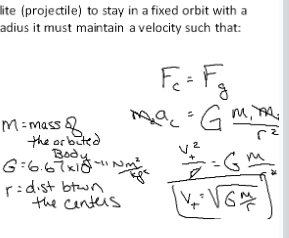
Newton’s Law of Universal Gravitation

Calculate the gravitational force on objects given mass and position

a_g/g = (R_E/r)²

^Where:

^{g = 9.80m/s2}

 ^{R_E = earth’s radius}

 ^{r = distance between center of earth and center of the object}

Gravitational Potential Energy, U_g

potential energy for object’s far from earth’s surface, like satellites; for two point masses separated by distance

Gravitational Potential Energy equation

U_g = (-Gm₁m₂)/r

 r = distance between earth’s center and the mass

As distance away increases, U becomes

less negative (closer to zero), meaning the object is free of the gravitational field

When to use different potential energies

Satellites in Circular Orbit

for a satellite (projectile) to stay in a fixed orbit with a constant radius it must maintain a velocity such that: F_c = F_g → v_t = sqrt(Gm/r)

What force holds a satellite in orbit?

centripetal force

Equation to determine speed of a satellite

v_t = sqrt(Gm/r)

Kepler’s 1st Law of Planetary Motion

Planets move in elliptical orbits with the sun at one of the focal points

Kepler’s 2nd Law of Planetary Motion

Speed of planets vary during their orbit, they move faster when closer to the sun. Remember conservation of energy.  When the potential energy changes, so does the kinetic energy

Kepler’s 3rd Law of Planetary Motion

The period squared is directly proportional to the radius cubed for planets orbiting the sun; T² = (4π²/GM)R³

Escape Velocity

the satellite’s velocity such that the mechanical energy of the satellite–central-object system is equal to zero; When the only force exerted on a satellite is gravity from a central object, a satellite that reaches escape velocity will move away from the central body until its speed reaches zero at an infinite distance from the central body.

Escape Velocity Equation

v_esc = √2GM/R

Why do astronauts on the I.S.S. not experience weight?

it travels around the Earth at such high speed, its travelling forwards equals out the falling and the ISS stays more or less at the same height

Perform calculations to determine a means to simulate gravity

stimulate by spinning; find v_t; use U_g equation or v_t equations