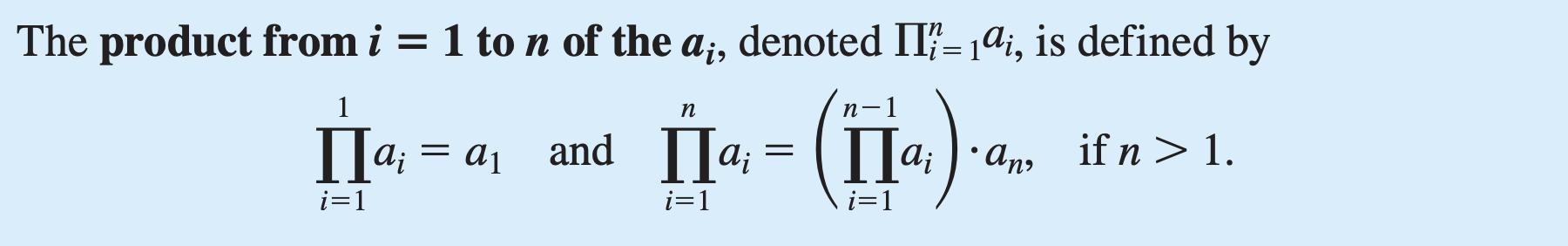Chapter 5 - Sequences, mathematical induction, and recursion

Sequence

A function whose domain is either all the integers between two given integers or all the integers greater than or equal to a given integer. Represented as a set of elements written in a row (a_m, a_m+1, a_m+2, ..., a_n).

each individual element a_k

Term ("a sub k")

The k in a_k

Subscript or index

Infinite sequence

A sequence that continues indefinitely, without a final term or limit.

Explicit formula (or general formula)

A rule that shows how the values of a_k depend on k.

The summation from k equals m to n of a-sub-k

The summation from k equals m to n of a-sub-k

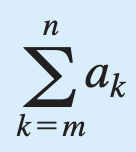
The sum of all the terms a_m, a_m+1, a_m+2, ..., a_n.

The expanded form of a sum

a_m + a_m+1 + a_m+2, ... + a_n.

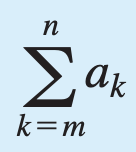
What are k, m, and n?

k is the index, m is the lower limit, n is the upper limit.

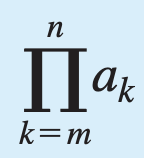
the product from k equals m to n of a-sub-k (if m and n are integers and m ≤ n).

The product from k equals m to n of a-sub-k

The product of all the terms a_m, a_m+1, a_m+2, ... , a_n.

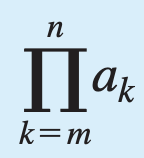
We write

a_m * a_m+1 * a_m+2 * ...* a_n

Recursive definition for the product notation

n factorial

n! (n is a positive integer)

0!

1

“n choose r” and represents the number of subsets of size r that can be chosen from a set with n elements (let n and r be integers with 0 ≤ r ≤ n).

Formula for computing

Principle of Mathematical Induction

Suppose the following two statements are true: P(a) is true and for every integer k ≥ a, if P(k) is true then P(k + 1) is true. Then the statement for every integer n ≥ a, P(n) is true.

Closed form

If a sum with a variable number of terms is shown to equal an expression that does not contain either an ellipsis or a summation symbol.

Geometric sequence

An ordered set of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the common ratio.

A recurrence relation for a sequence a0, a1, a2, ...

A formula that relates each

term ak to certain of its predecessors ak−1, ak−2, ... , ak−i, where i is an integer with k - i ≥ 0.

Initial conditions

The starting value(s) for a sequence.

The summation from i = 1 to n of the a_i

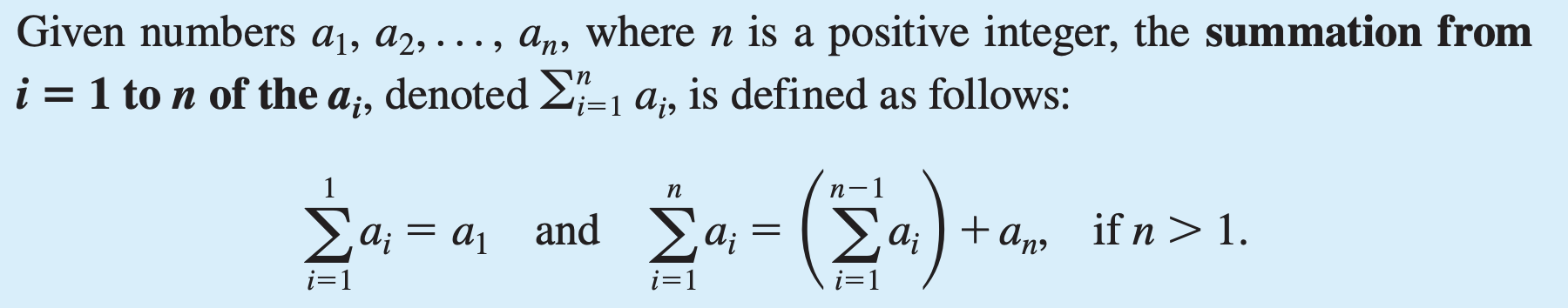
The product from i = 1 to n of the a_i

Iteration

The process of repeatedly applying a function or algorithm, where the output of one step becomes the input for the next, until a specific condition is met.

Arithmetic sequence

A sequence of numbers where each term is formed by adding a constant value, called the common difference, to the preceding term.