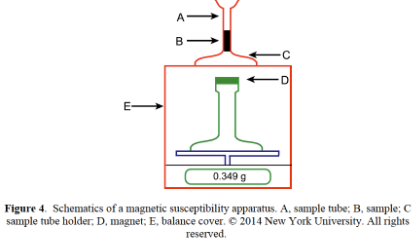
Magnetic Susceptibility

ferromagnetism

significant attraction to a magnetic field and capable of making magnetic field of its own

ex. iron, nickel, cobalt, -16°C gadolinium, other cold alloys

ordinary magnetism

all substances posses some ability to react to a magnetic field; 10³ to 10⁶ times weaker than ferromagnetism

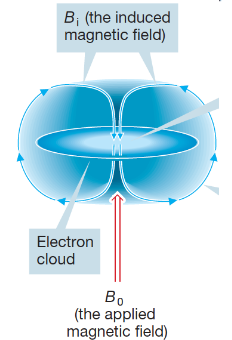
diamagnetic

magnetic dipole moment per unit volume is antiparallel to the field; paired electrons; present in all substances, no net mag. moment because all spins cancel out; temperature independent

in external field, induction causes internal current due to the change in the electron orbital angular momentum; this current opposes the ex. field

ex. bismuth

paramagnetic

magnetic dipole moment per unit volume is parallel to the field; unpaired electrons; permanent mag. moment; electron spins and orbital angular moments are not zero; temperature dependent

in external field, moments tend to line up with the mag. field; relatively small force

ex. odd # electrons, free atoms and ions with partially filled inner shell, molecular oxygen, organic biradicals, metals

Ferromagnetic phenomena

exhibits a net magnetic moment (spontaneous magnetization) even in the absence of an external magnetic field; Electron spins (magnetic moments) are arranged in a regular (parallel) pattern due to magnetic interactions between them (nearest neighbor)

magnetic interaction

any dependence of the energy of 2 or more moments on their relative orientations; orginates from electrostatics not magnetism

no magnetic interactions in the absence of external field

Individual mag. moments point in random directions due to thermal motions, no net mag. moment

Antiferromagnetic phenomena

mag. moments (spins) are ordered in an antiparallel arrangement; no net total mag. moment (in the absence of an external field); magnetic interactions favors antiparallel orientation of neighboring moments

ex. MnO and Cr

Magnetism and temperature

spontaneous magnetization decreases with increasing temp. and vanishes above a certain critical temp.

So, ferro- and antiferromagnets display their properties below their critical temp.

Can magnetism be explained by classical/statistical mechanics?

NO! Classic system in thermal equilibrium cannot display a magnetic moment

partition function

describes the statistical properties of a particular system in thermodynamic equilibrium

Bulk Magnetism

induced magnetisation depends on strength of magnetic field

M=χB

M = magnetic moment per unit volume

B = external magnetic field

χ = magnetic susceptibility per unit volume/volume susceptibility/induced moment per unit volume per unit applied field

• >0 for paramagnetic

• <0 for diamagnetic

mass susceptibility

induced moment per unit mass per unit applied field (m³kg^-1)

χ_w = χ/ρ

ρ = density

molar susceptibility

induced moment per mole per unit applied field (m³mol^-1)

χ_w = ℳχ_{w = V}χ

ℳ = molar mass

V = molar volume

Macro- and microscopic magnetic properties

magnetic moemt of atom results from

1. electron spin - paramagnetic

2. orbital angular momentum of electrons about the nucleus - paramagnetic

3. change in the orbital momentum induced by an external magnetic field - diamagnetic

since diamagnetic term is so small, μ_m=797.1μ_Bsqrt(Tχ_m)

assume μ_m=μ_S, μ_S=μ_Bsqrt(n(n+2))

Hund’s rules

electronic orbitals are filled according to these; gorund electronic state characterised by

1. maximum value of the total spin S allowed by the exclusion principle

2. max. value of the total orbital angular momentum L consistent with value of S

3. Value of the total angular momentum J is

   1. equal to |L-S| when the shell is less than half full

   2. equal to L+S when shell is more than half full

   3. equal J=S when the shell is half full (since application of first rule gives L=0)

Spin paramagnetism

odd # electrons OR even # if degen. electronic level is only partially filled

S=n/2, when there are n electrons in the given orbital and n≤2l+l

permanent mag. dipole moment μ_s = g₀μ_Bsqrt(S(S+1)) = μ_Bsqrt(n(n+1))

μ_B = ℏe/2m

Orbital paramagnetism

arises from orbital angular momentum; electron in orbital with 1+ units of angualr momentum behaves like an electric current in circular wire = produces mag. moment; when all orbitals equally filled = orbital moments cancel out; may arise but be cancelled out by neighbouring atom/ion interaction; neglible contribution

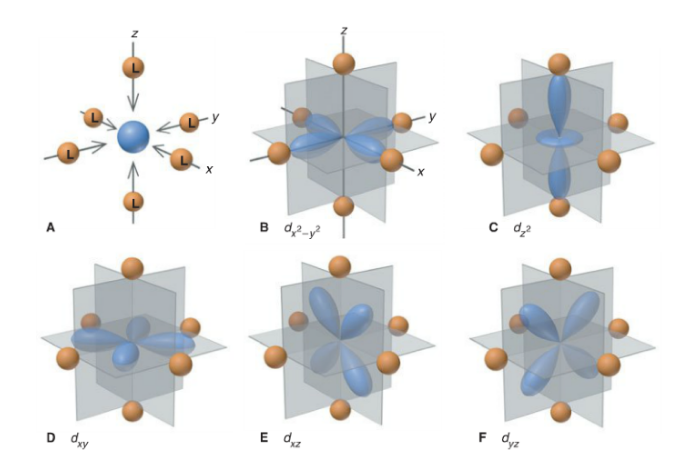
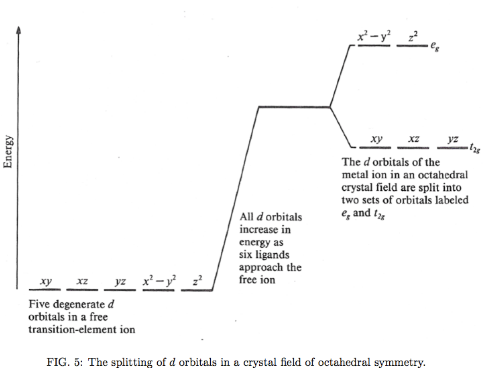
Transition metal complexes

metal surrounded by negative or neutral ligands

free transition element ion = 3d subshell has 5 degen. d orbitald

complex ion = ligands form electrostatic crystal field of high (octahedral) symmerty about the central metal ion; remove degeneracy

electronic balance

diamagnetic = repel = Δm>0

paramagnetic = attract = Δm<0