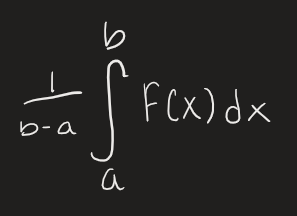BC Definitions and Some AB

bc and ab basic shit

Integration By Parts

∫udv = uv -∫ [vdu]

Geometric Series

infinite series of ar^n
a= first term, r =common ratio
from n=0 to infinity of ∑ ar^n

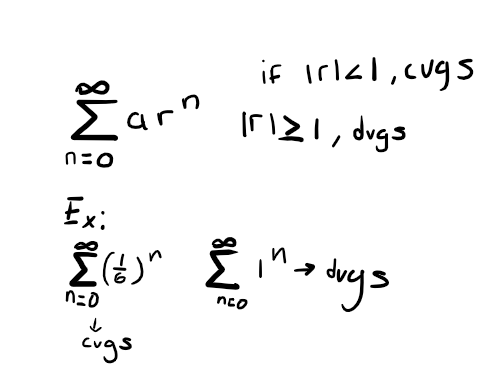
Taylor Series Formula

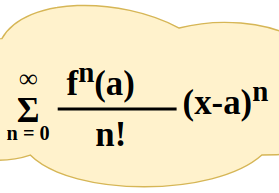
Maclaurin Series Formula

• Maclaurin series is a Taylor series but not vice versa

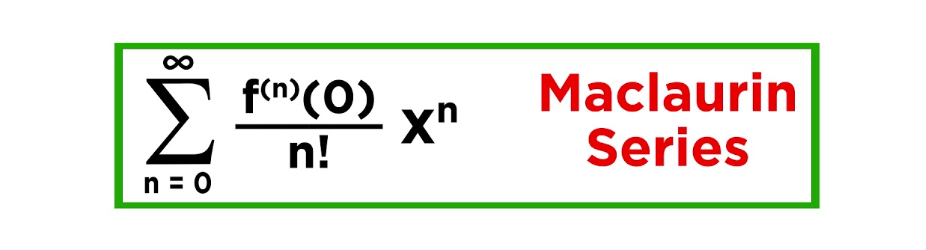
sin(x) Maclaurin Series

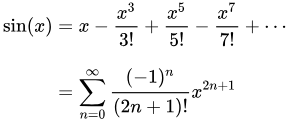
cos(x) Maclaurin Series

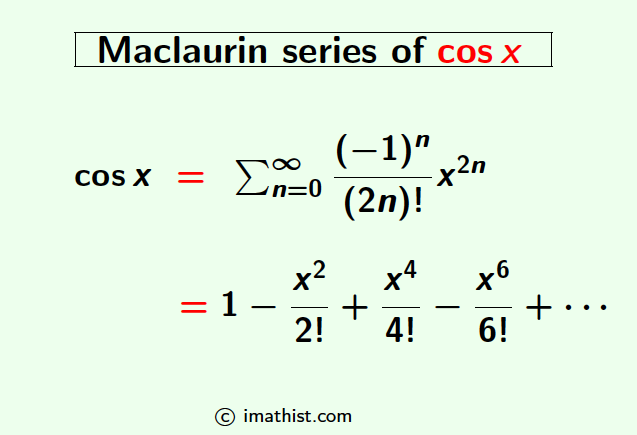
1(1+x) Maclaurin Series

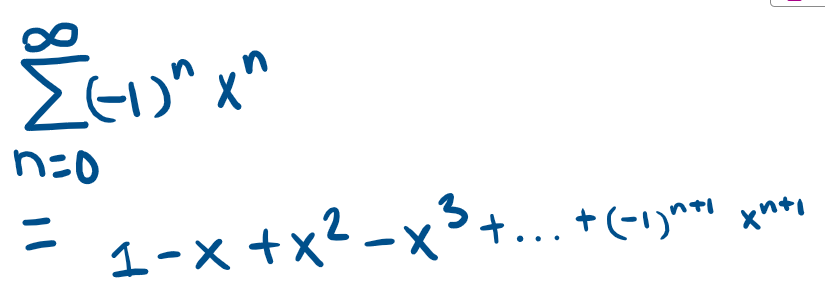
arctan(x) Maclaurin Series

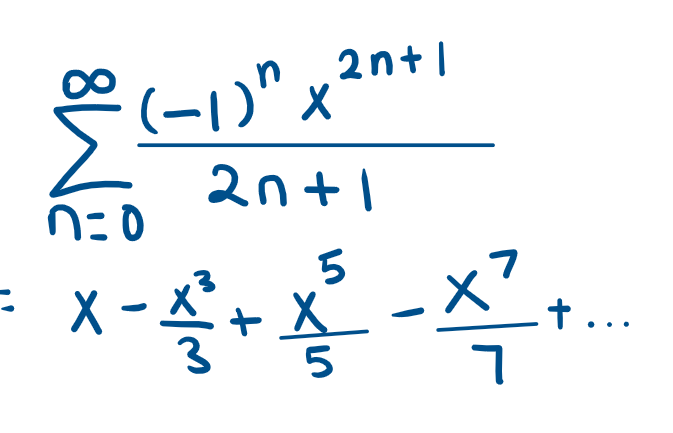
1/(1-x) Maclaurin Series

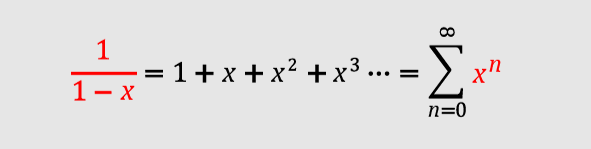
ln(1+x) Maclaurin Series

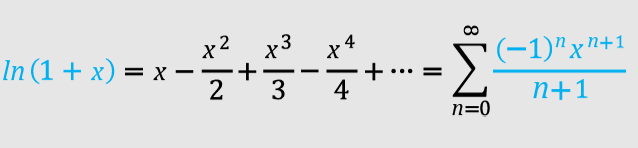
e^x Maclaurin Series

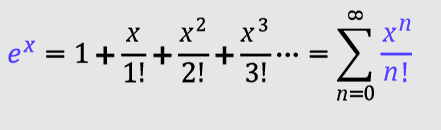
Lagrange Error Bound

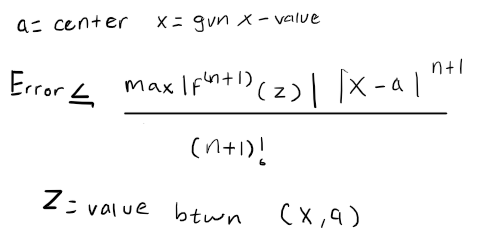
Alternating Series Error Bound

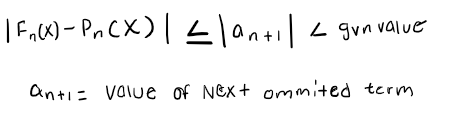
Divergence/nth term test

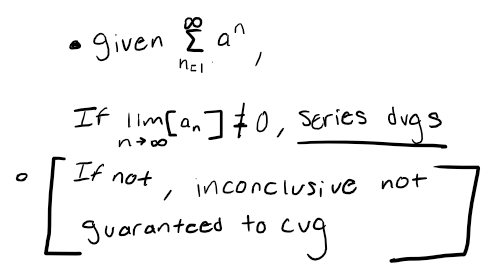
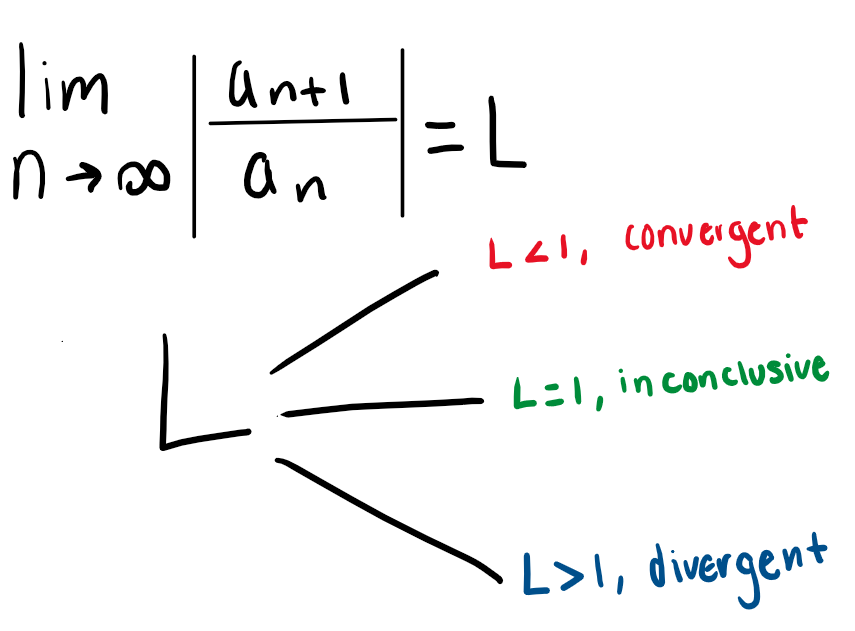
Ratio Test

nth Root Test

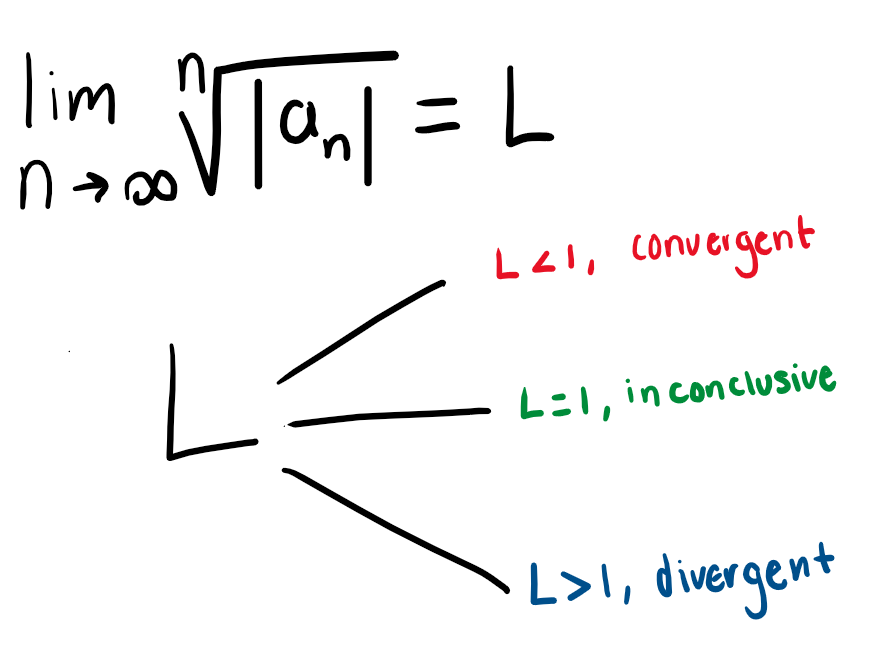
Integral Test

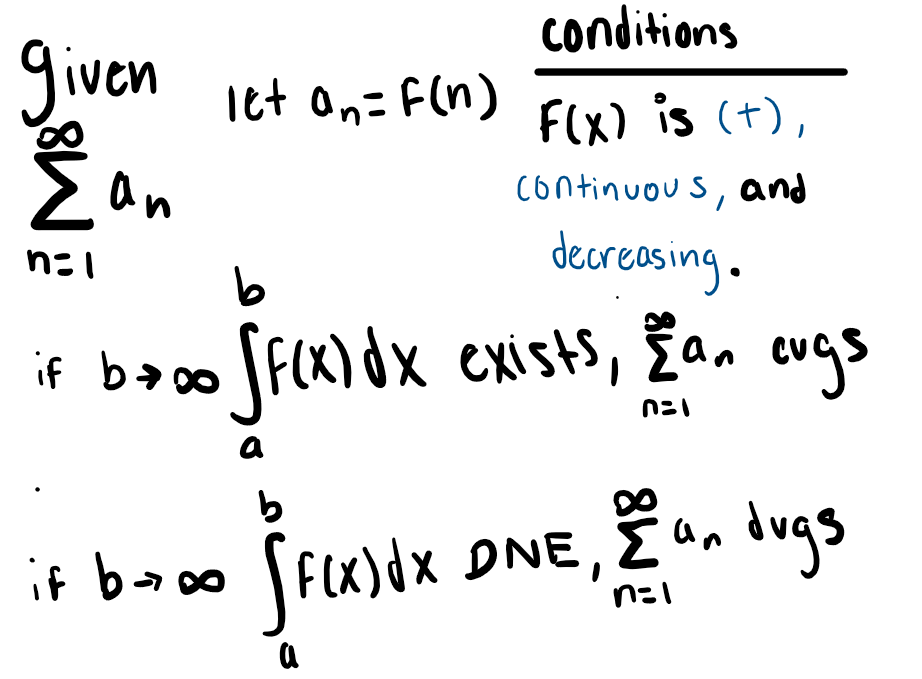
Alternating Series Test

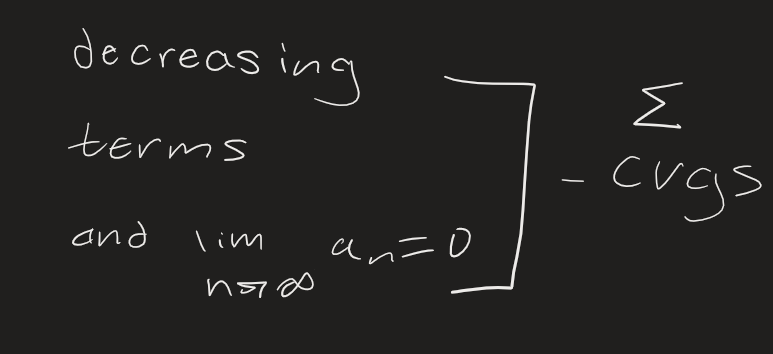
P-series Test

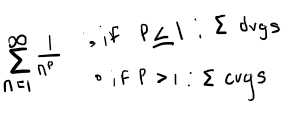
Direct Comparison Test

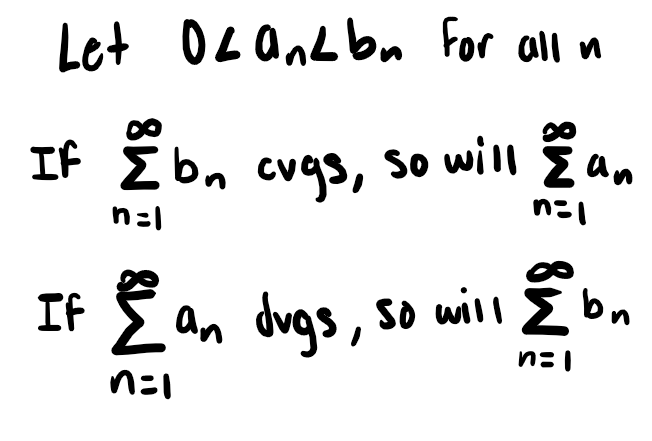
Limit Comparison Test

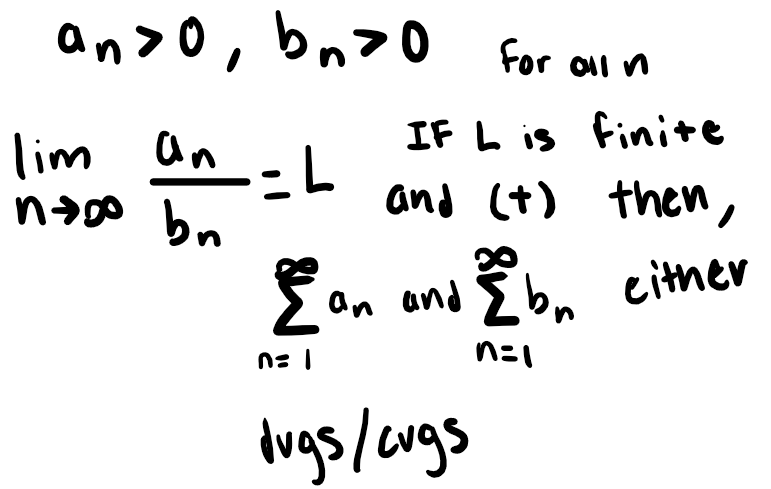
Absolute Convergence Test

Power Series General Form

In Polar Cords what is x and y equal to?

tanθ = ?

x = rcos(θ) y= rsin(θ)

tan(θ) = y/x

Also

• r² = x²+y²

• θ = tan-1(y/x)

Area for Polar Curve

A = ½ ∫r²dθ

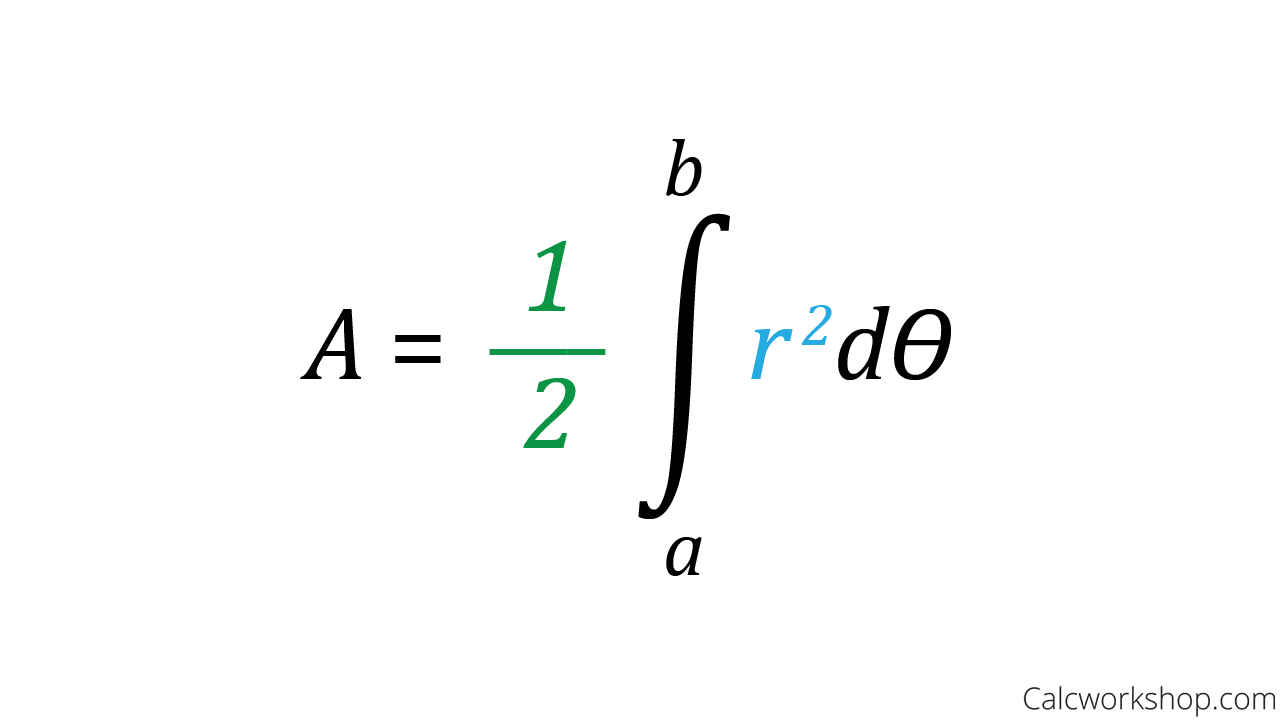
slope for a polar curve

dy/dx = (dy/dθ)/(dx/dθ)

Slope for a parametric curve

dy/dx = (dy/dt)/(dx/dt)

Second derivative of a parametric curve

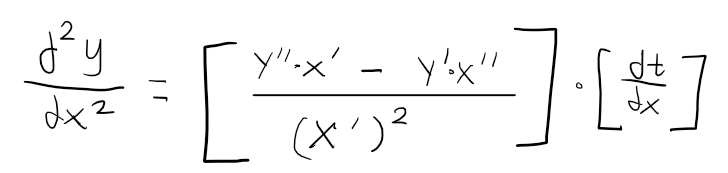
Position, Velocity and Acceleration Vectors.

• P = <x(t), y(t)>

• V =<x’(t), y’(t)>

• A = <x’’(t), y’’(t)>

Arc Length Formula

Remember Arc length parametric terms is simply distance formula

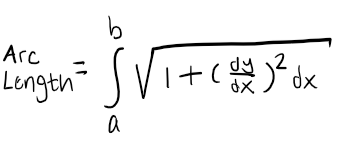
Speed Formula

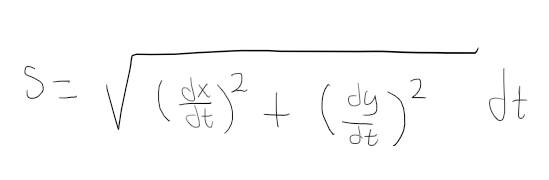
Distance Formula

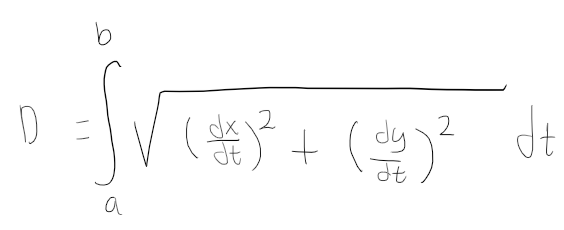
When is the Particle moving to the left and moving to the right?

Velocity = (-) , left

Velocity =(+), right

When is the particle speeding up/moving away from origin?

When Velocity and Acceleration are the same sign

Logistic Differential Equation General Form

dp/dt = kP(1 - P/C)

• P = population at time t

• C = carrying capacity

• k = constant

Logistic Solution Form

P = c/(1+Ae^-kt)

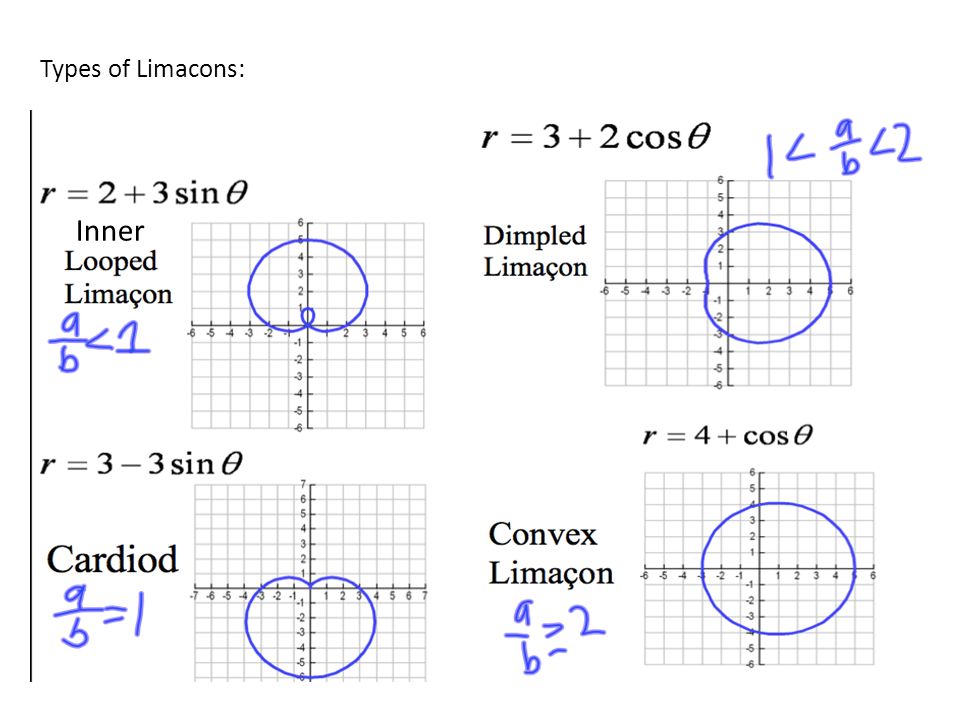
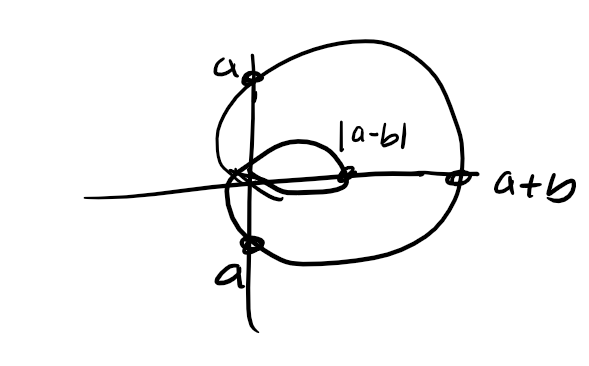
Limacons Variations and General Equation

r = a±bcosθ or r = a±bsinθ

• Inner Loop

• Cardioid

• Dimpled

• Convex

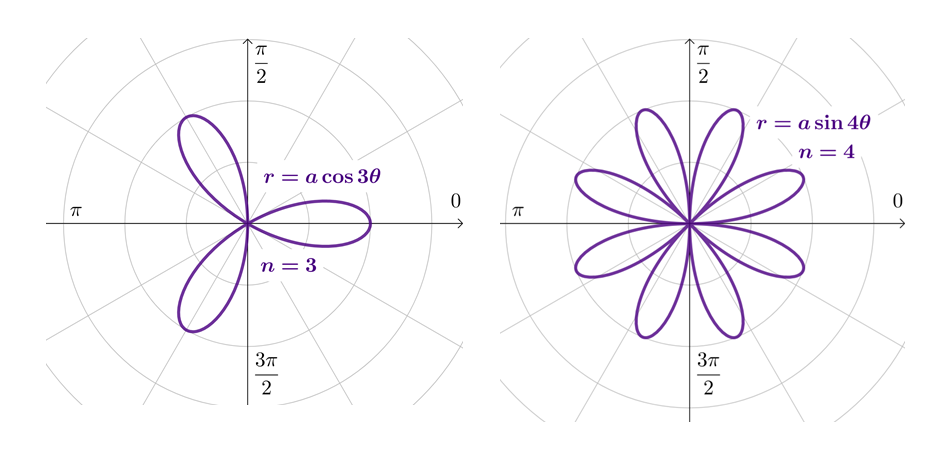
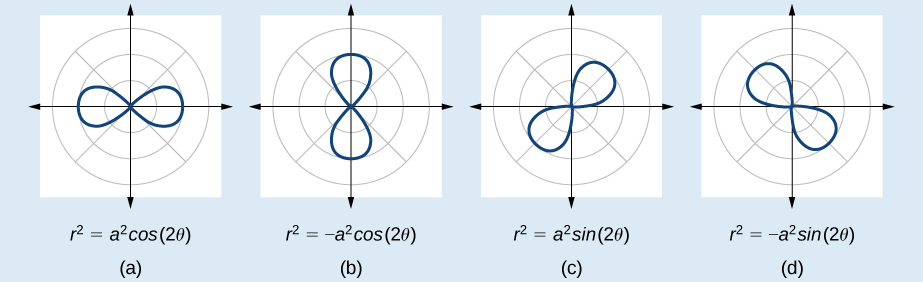
Rose Curves and General Equation

acos(nθ) or asin(nθ)

• If n is odd, there are n petals

• If n is even, there are 2n petals

First petal positions:

• Cos curve - On the x-axis

• Sin curve - First Quadrant

Limacon Inner Loop Points

Leminiscate General Equation

r = a²sinθ or a²cosθ

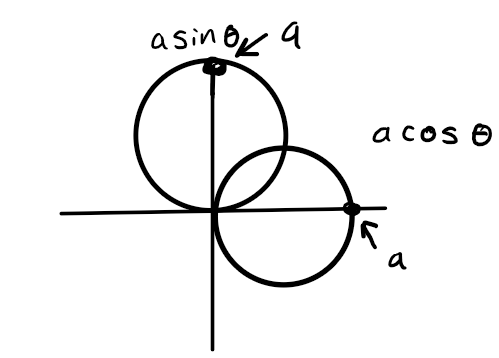
Circle General Equation

r = acosθ or asinθ

Spiral General Equation

r = θ

Infinite Sum

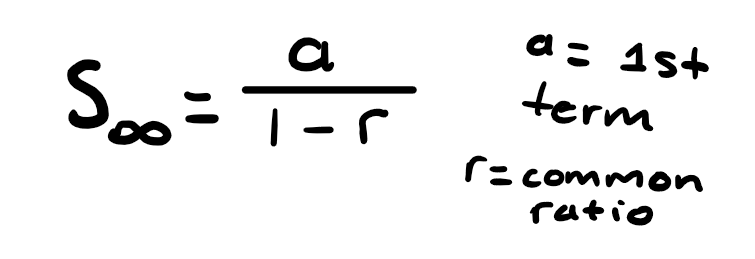
Finite sum

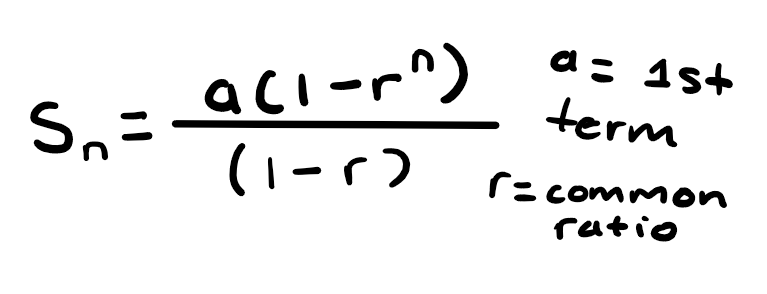
Telescoping Series

First and last term are the only remaining terms within series.

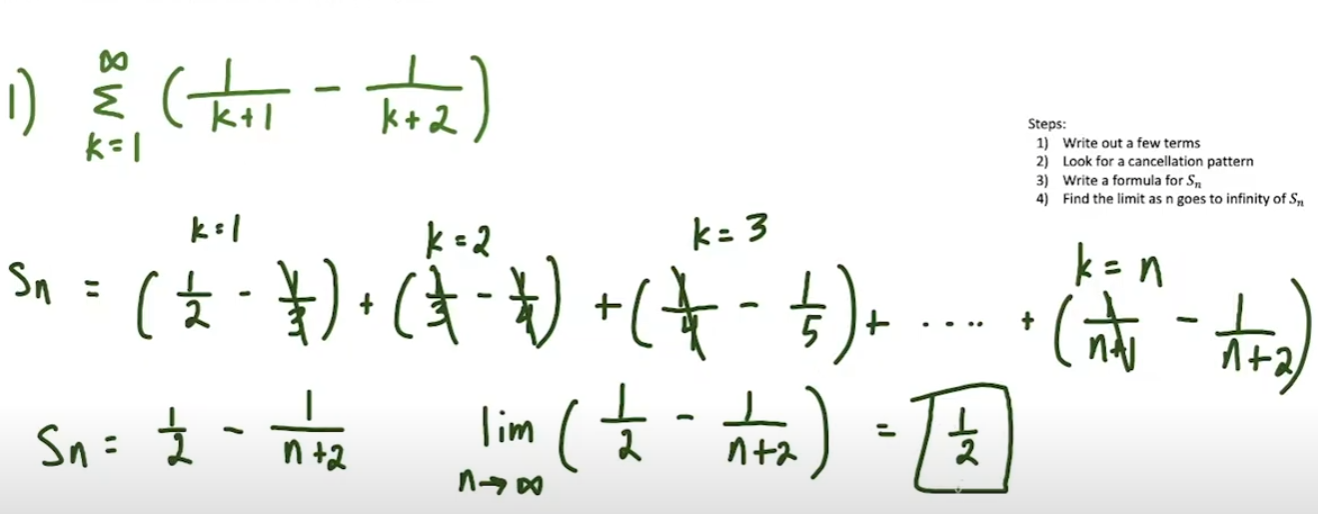
Euler’s Method

Inflection Point/POI

f’’(x) =0 or und and changes sign

Critical Point

f’(x) = 0 or und

Relative Min/Max

Min: f’ changes from (+) to (-) and f’ = 0 or und

f’ changes from (-) to (+) and f’ = 0 or und

What does concave up/down mean?

f’’ > 0 for concave up, f’’<0 for concave down

Tangent Line Eq/ Normal Line eq

Tangent Line: y-y1=m(x-x1)

Norm Line: y-y1=1/m(x-x1)

Riemann Sums

Right hand - overestimate for increasing functions and under for decreasing functions

Vice versa for Left hand

The Trapezoidal sum is the same as the average of the left and right Riemann sums (Goldilocks for estimating)

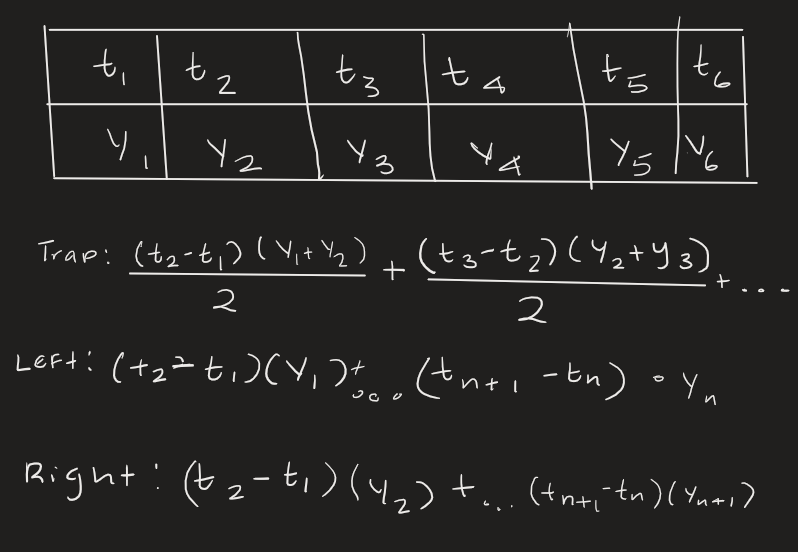
MVT

continuous on [a,b], and differentiable on open,

then exists x=c where f’(c ) =f(b)-f(a)/(b-a)

EVT

If F(x) is continuous on [a,b], then f has both an abs minimum and an abs max

IVT

If f(x) is continuous on [a,b], and k is between f(a) and f(b), and a<C<b then F(C) = k

Cross Section Volume Identities

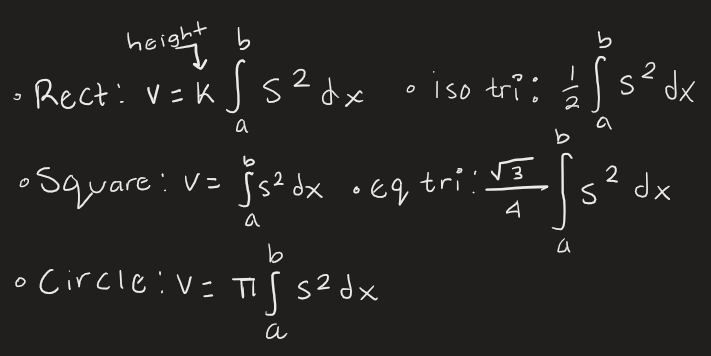
Avg Value