Circle Theorems

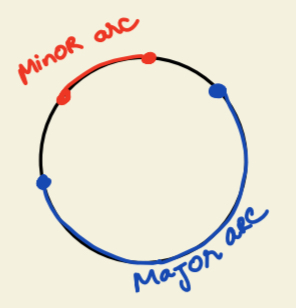
Minor Arc, Major Arc

Major arc >180

Minor arc < 180

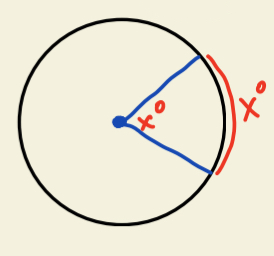
Central Angle

Central angle has the same measure with the arc

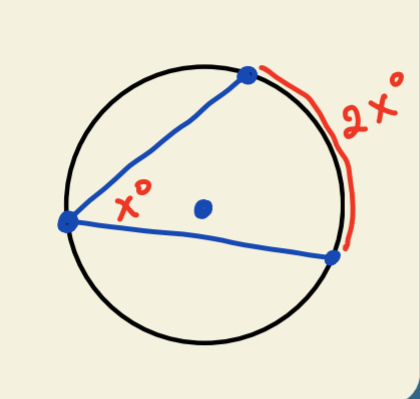
Inscribed Angle

Inscribed angle is half the arc

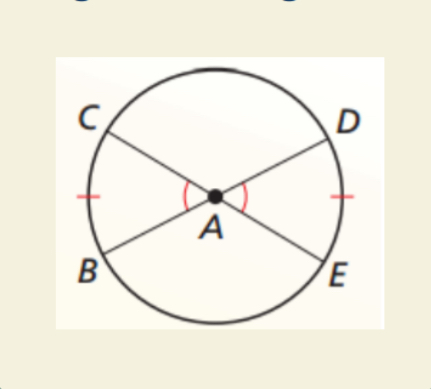
Congruent Central Angles Theorem

Minor arcs congruent iff corresponding central angles are congruent

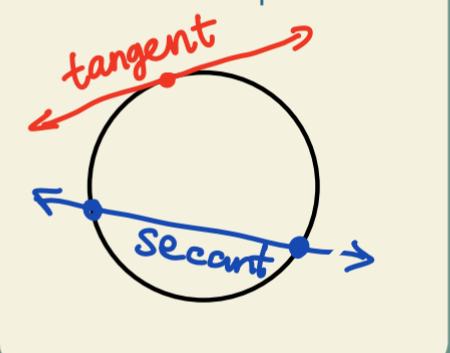
Tangent Line & Secant Line

Tangent line cuts the circle at 1 point Secant line cuts the circle at 2 points

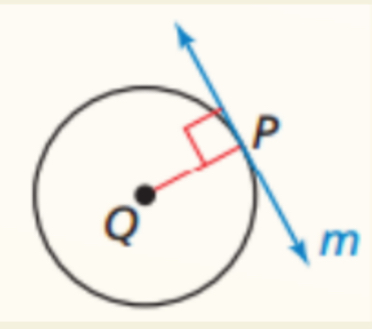
Tangent Line to Circle Theorem

Tangent line is perpendicular with radius

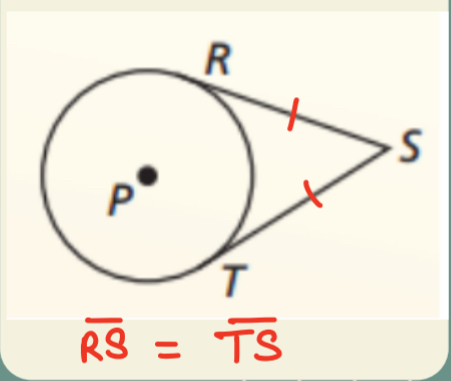
External Tangents Congruent Theorem

Tangent segments from external point are congruent

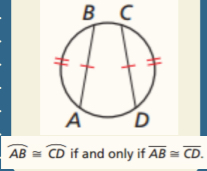
Congruent Corresponding Chords Theorem

2 minor arcs congruent iff corresponding chords are congruent

Perpendicular Chord Bisector Theorem

Diameter perpendicular to chord then diameter bisects chord & its arc

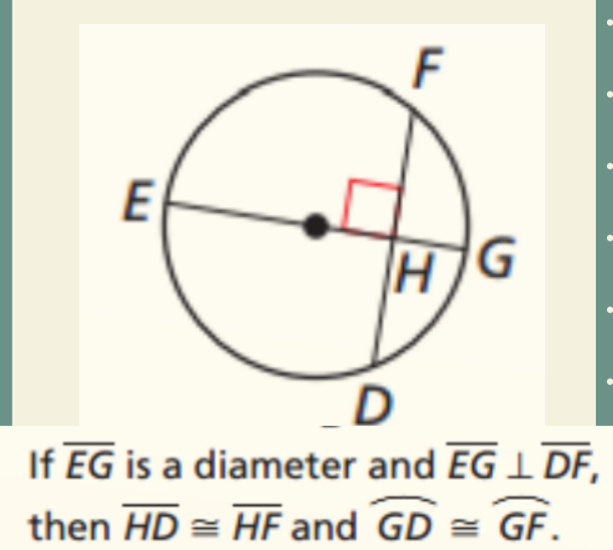
Perpendicular Chord Bisector Converse

1 chord is perpendicular bisector with another chord then first chord is a diameter

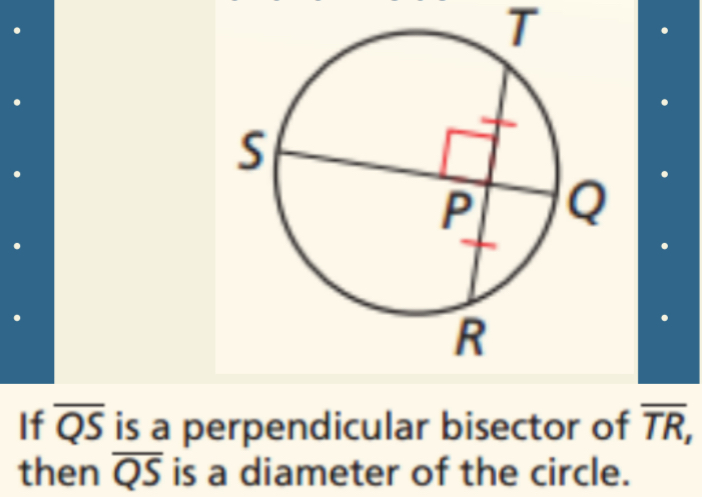
Equidistance Chords Theorem

2 chords congruent iff distance from center to chord are congruent and perpendicular.

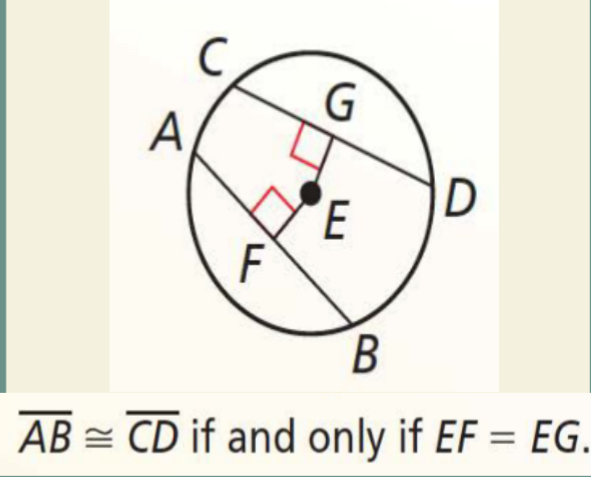
Inscribed Right Triangle Theorem

The angle in a semicircle subtended by the diameter is a right angle

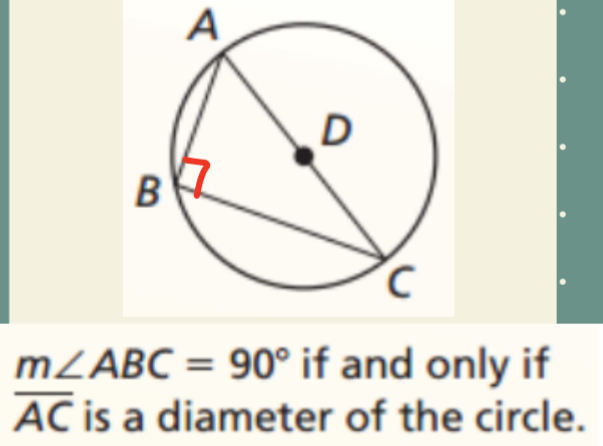
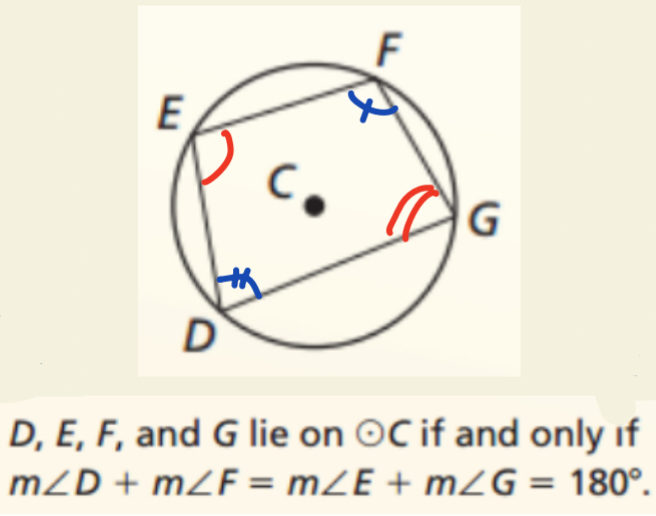
Inscribed Quadrilateral Theorem

Opposite angles quadrilateral sum = 180°

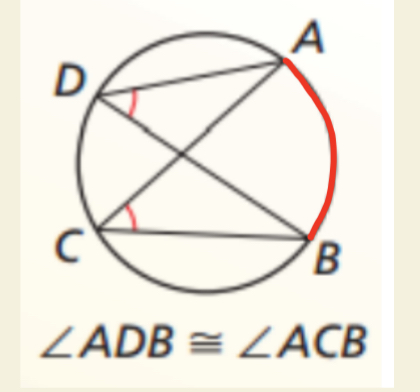
Inscribed Angles Theorem

Angles subtended by the same arc in a circle are equal.

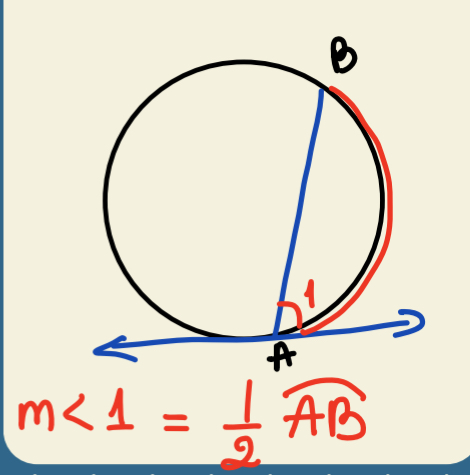
Tangent and Intersected Chord Theorem

Angle is 1/2 of intercepted arc

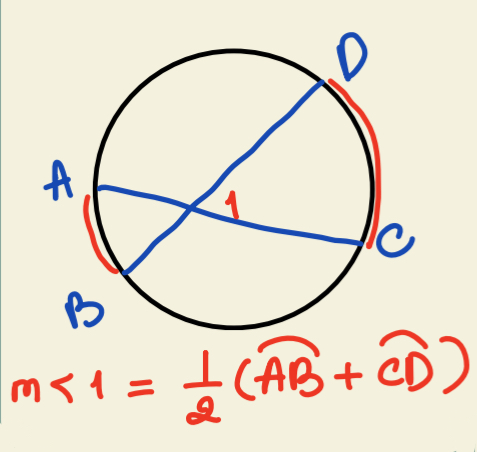
Angles Inside Circle Theorem

Angle is half of sum of the arcs

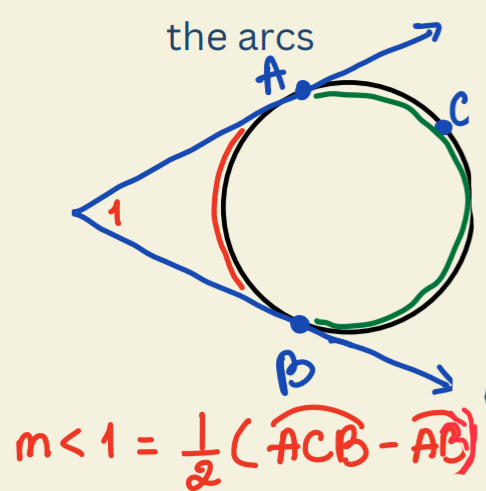
Angles Outside Circle Theorem

Angle is half of the difference between the arcs

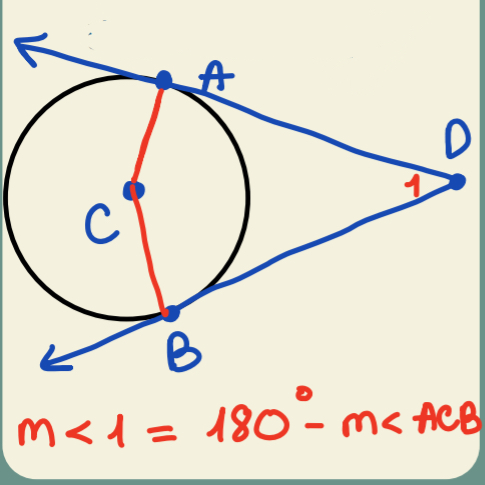
Circumscribed Angle Theorem

Circumscribed angle is equal to 180 minus the central angle

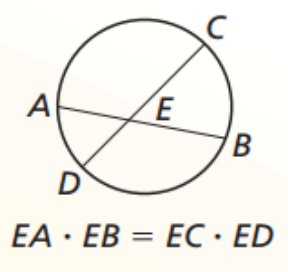
Segments of Chords Theorem

Part x Part = part x part

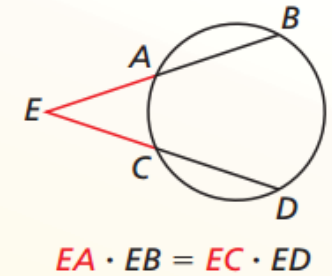
Segments of Secants Theorem

(Outside) part x whole = (Outside) part x whole

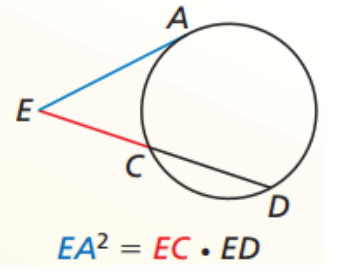
Segments of Secants and Tangents Theorem

tangent² = Part x Whole (secant)

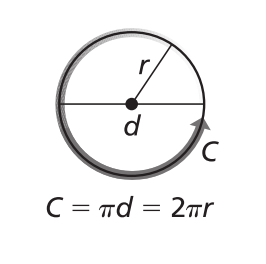
Circumference of Circle

C = 𝝅d = 2𝝅r

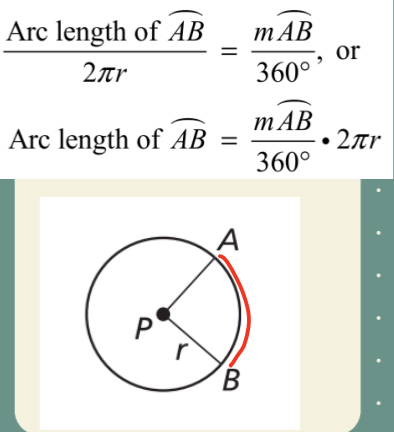
Arc Length

Arc length of AB.

_______________. = mAB/360°

2𝝅r

Or

Arc length of AB = mAB/360° x 2𝝅r

Area of Circle

A = 𝝅r²

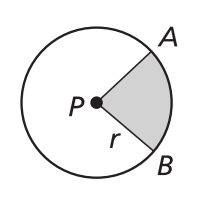
Area of a Sector

Area of sector APB/ 𝝅r² = mAB/360°

Or

Area of sector APB = mAB/360° x 𝝅r²

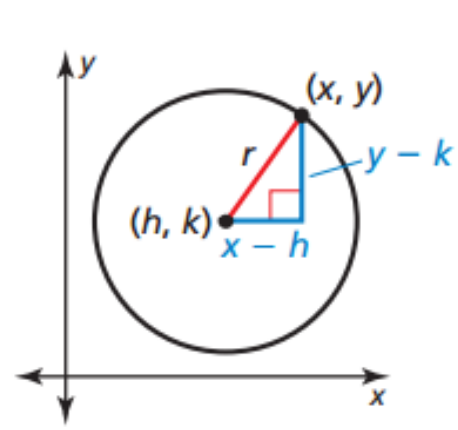
Standard Equation of Circle

Center (h,k) and radius r

(x — h)² + (y — k)² = r²

Radians to Degrees

Degrees to Radians