Central Tendency

Central Tendency

• A statistical measure that describes a single score that is the center of a distribution

• Goal is to find the single score that is most typical or most representative of the entire group

Characterised in 3 ways:

1. The point of which a distribution would balance

2. The value who’s average absolute deviation from all other values is minimised

3. The value who’s squared deviation from all other value is minimised

Measures of Central Tendency

MEAN: X̄ = ∑X / N

MEDIAN: The point at or below which 50% of the scores fall when the data are arranged in numerical order

MODE: The most common score; also can be identified as the highest point in a distribution

Mean

The amount of X each individual would get if the total (∑X) were divided equally among all the individuals (N)

FORMULA) X̄ = ∑X / N

• Computed by adding all the scores (the sum ∑X/∑fX) and dividing by the number of scores (N)

• Population mean: μ

• Sample mean: X̄ or M

Weighted Mean (Calculating the Overall Mean)

• Overall mean

X̄ = ∑X (Overall sum for the combined group) / N (Total number of scores for the combined group)

Characteristics of the Mean

• Changing a score

  • Changes the mean

• Introducing or Removing a score

  • Usually changes the mean

• Adding or Subtracting a constant from each score

  • Same constant is added/subtracted to/from the mean

• Multiplying or Dividing each score by a constant

  • Mean changes the same way

  • Common way to change the unit of measurements

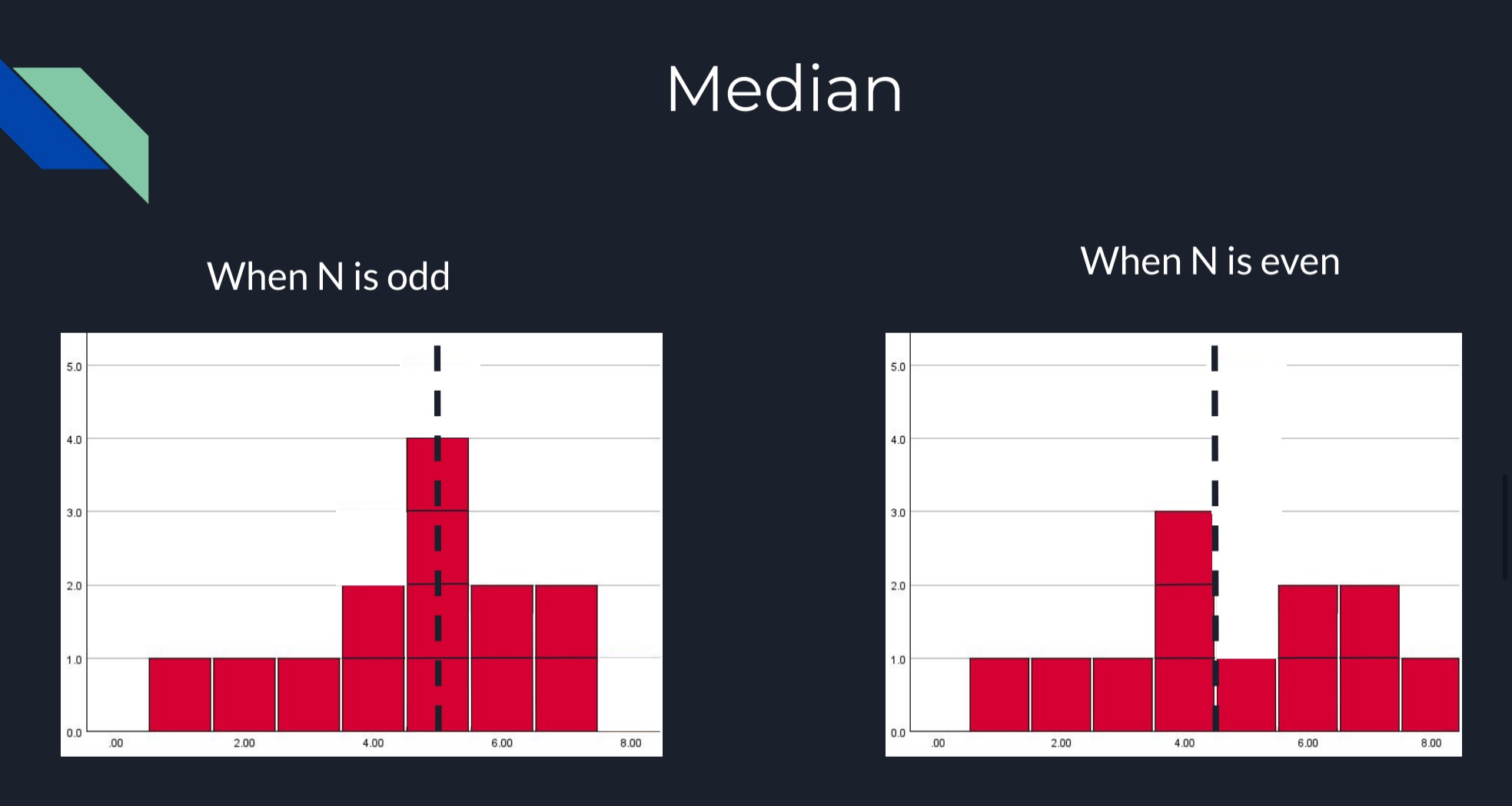
Median

• The score that divides the distribution in half so that 50% of the individuals in a distribution have scores at or below the median

• The scores are divided into equal-sized groups

EXAMPLE)

N (population) ODD: 1, 2, 4, 5, 6

N (population) EVEN: 1, 2, 4, 4, 5, 6

Mode

• The score or category that has the greatest frequency

• Can be used with any scale of measurement

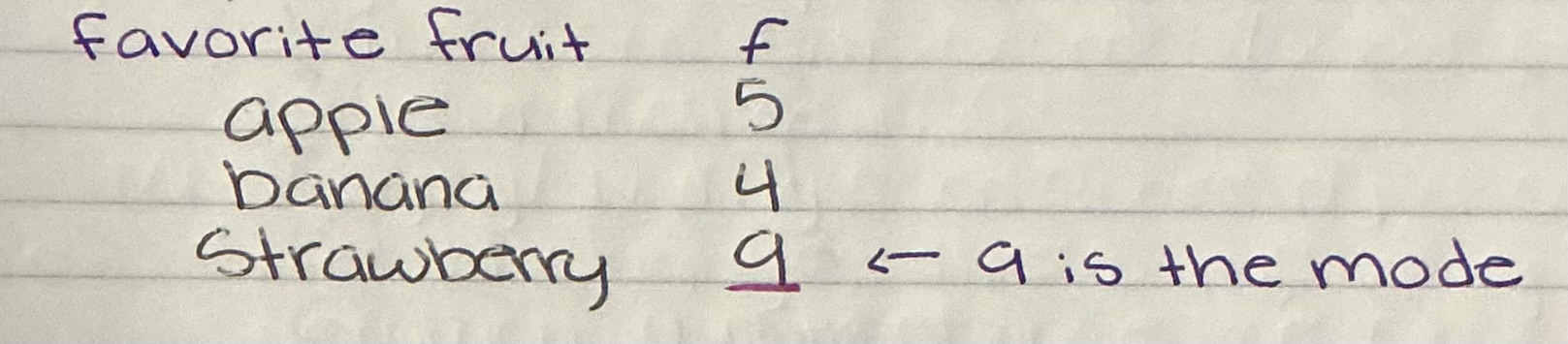
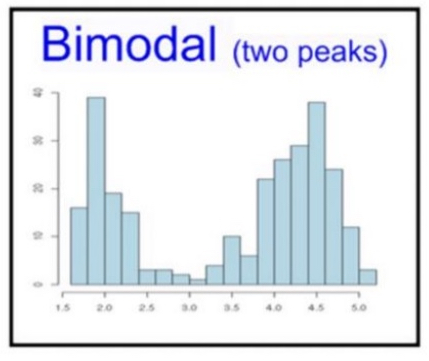
Bimodal

• Has two peaks

Multimodal

• Has many peaks

Unimodal

• Has one peak

No Mode

• Same level (rare)

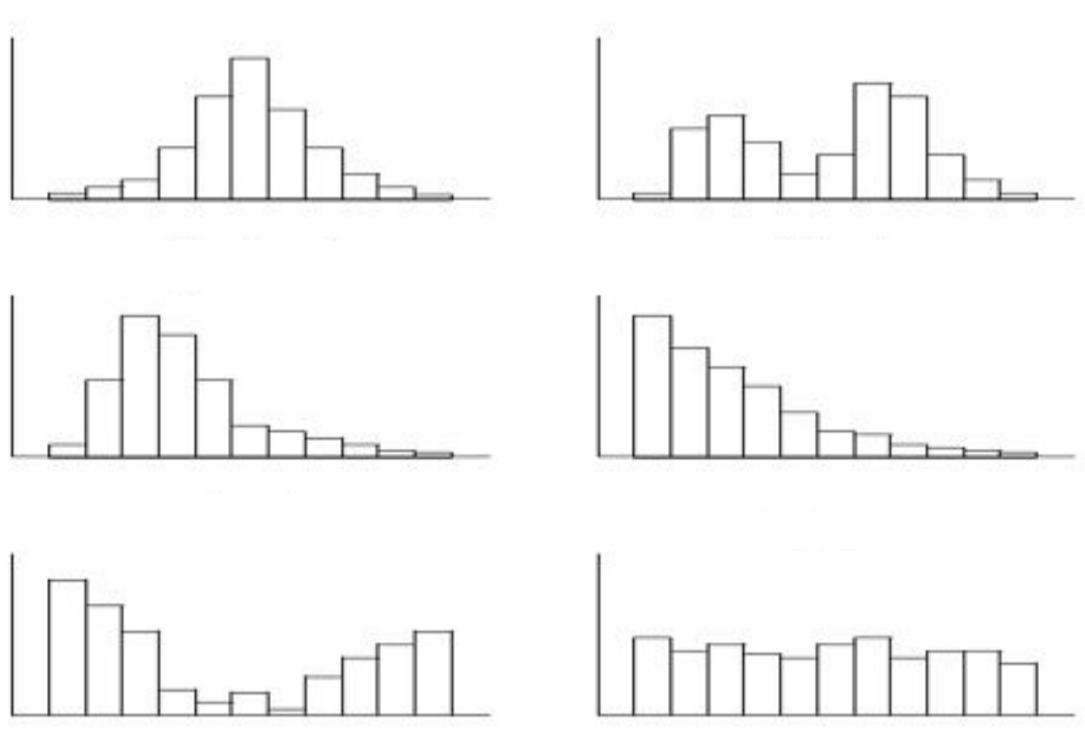
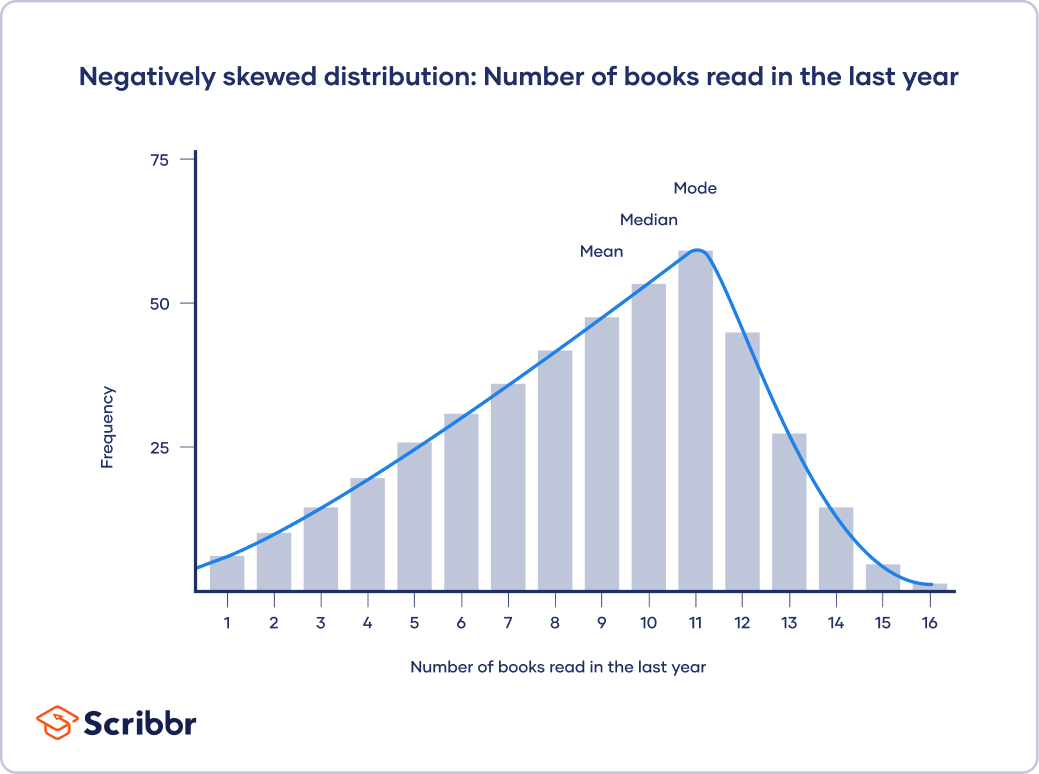
Central Tendency and the Shape of the Distribution (SKEWED)

• Skewed Distributions

All examples of distributions shown in image example

Central Tendency and the Shape of the Distribution (SYMMETRICAL)

• Symmetrical Distributions

All examples of distributions shown in image example

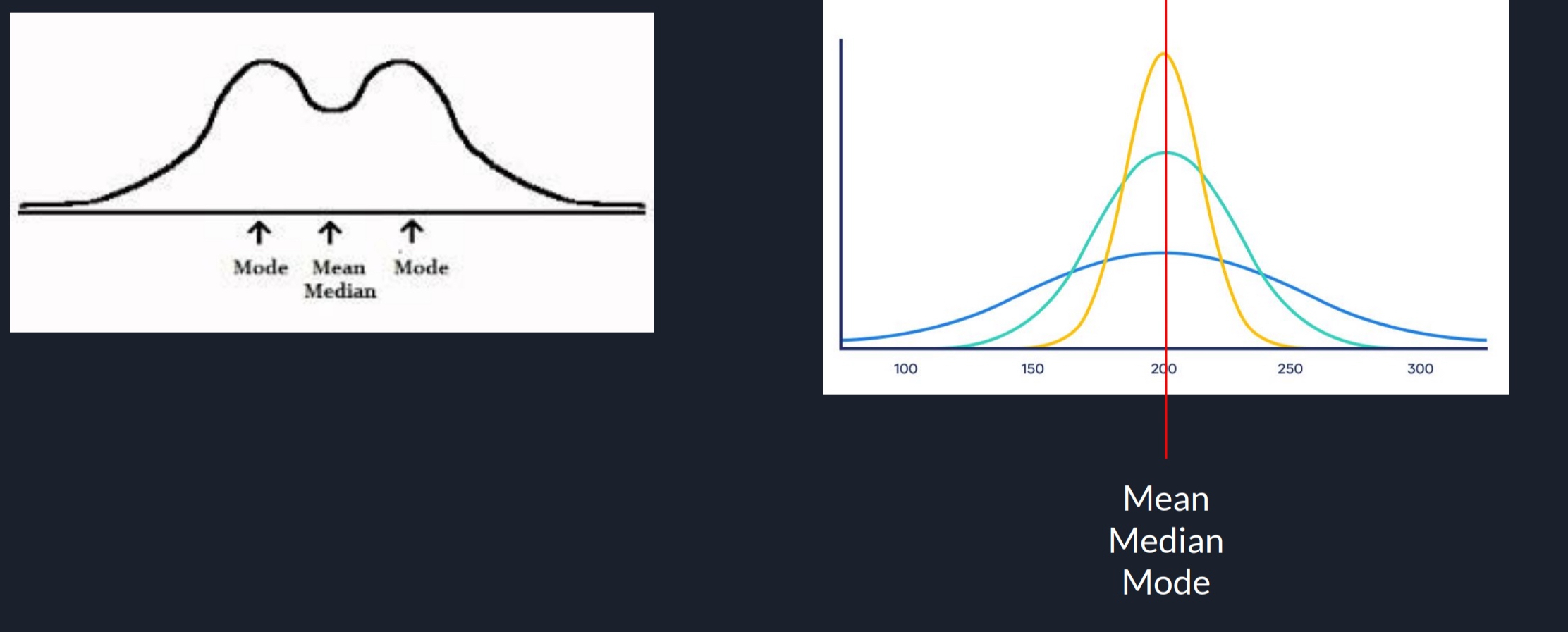
When to Use the Median (1)

Extreme scores or skewed distributions

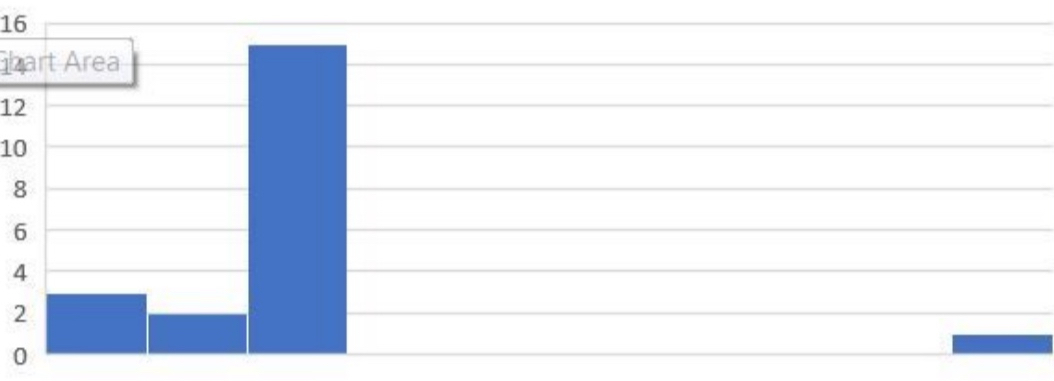
When to Use the Median (2)

Undetermined Values

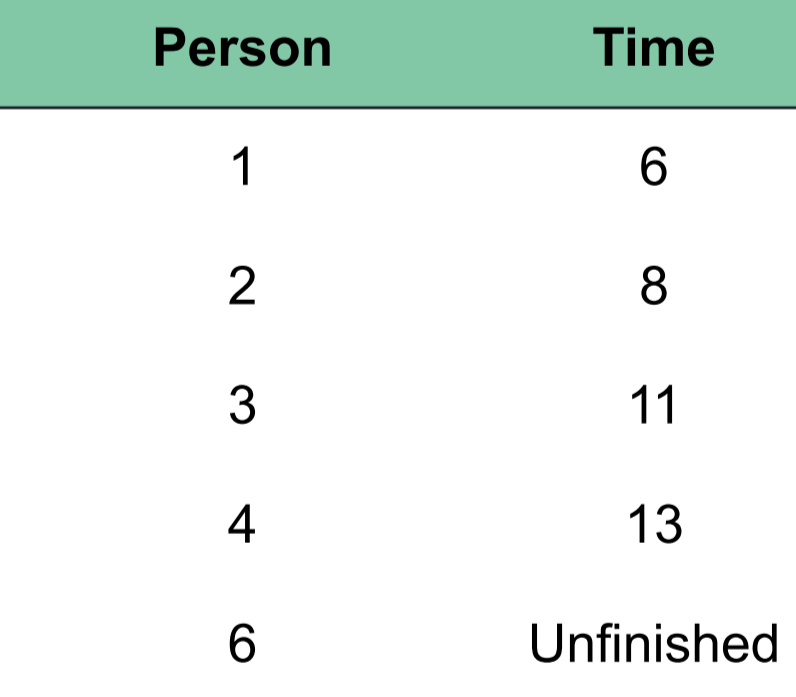
When to Use the Median (3)

Open-ended Distributions

• NO upper(shown in example) or lower limit for one of the categories

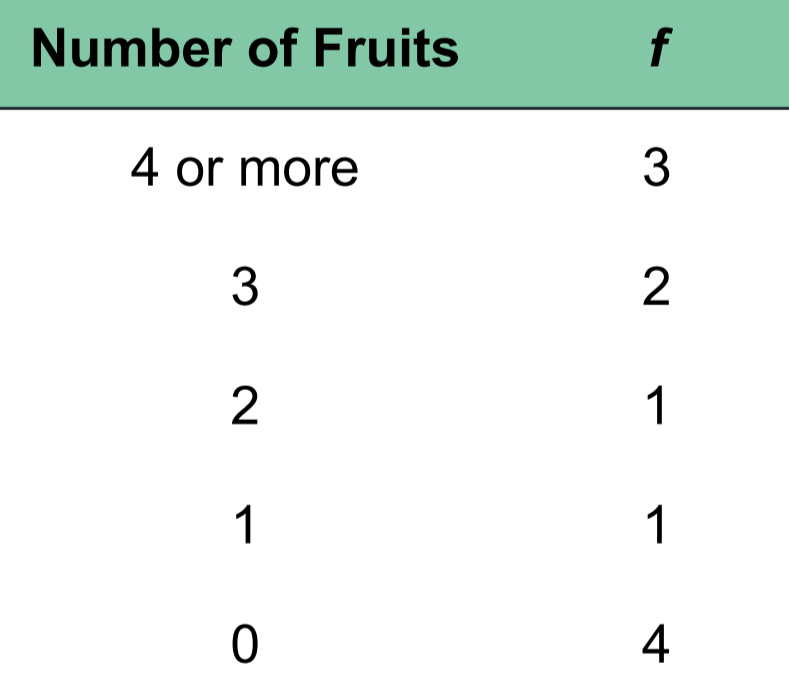
When to Use the Median (4)

Ordinal Scales

• Determined direction but not distance

When to Use the Mode

• Nominal scales

  • Impossible to compute a mean or median

  • Mode is the only option

• Discrete variables

  • Mode always identifies the most typical case

• Describing shape

  • Gives an indication of the shape of the distribution