quadratic equations and functions pt I

Quadratic equations

ax² + bx + c = 0, where a is not equal to 0

How to solve equations with square terms

Inverse operations, take the square root out of booth sides,

x² = 49

x = 7, -7

How to solve these equations without a perfect square?

Take square root out of both sides, the number that is not a perfect square can be simplified. Find a multiple that is a perfect square and simplify

The square root of 8 = the square root of 4 • the square root of 2 = 2 • the square root of 2

the square root of a•b can be simplified as what

The square root of a times the square root of b

The quadratic equation of ax² + bx = 0 always has

Two solutions, one of them being zero

5x² +15x = 0

5x(x+3) =0

Using the zero product rule,

5x = 0, x = 0 x+3=0, x = -3

Zero product rule

If A and B are any two quantities such that AB = 0, then A = 0, B = 0, or that both A and B are equal to 0

Grouping method

Find factors of ac whose sum is b

Rewrite equation to put factors on separate sides

Group terms and find GCF of each group

Factor out the common factor

Set each factor equal to 0

Perfect square trinomials have how many solutions

1

Difference of squares have how many solutions

2, one being the opposite of the other but same absolute value

To complete the square,

Factor the perfect square trinomial, take square root of both sides and then solve for x

(x+7)² =121

x +7=11,-11

x =4,-18

To turn a quadratic equation in the form ax² + bx + c where a =1,

Add (b/2)² to BOTH sides AFTER MOVING THE CONSTANT TO THE RIGHT SIDE OF THE EQUATION. If a is not equal to 1, divide the equation by a AFTER ISOLATING THE CONSTANT but BEFORE ADDING (b/2)²

Parabola

The graph of a Quadratic function

The vertex of a parabola

The point in a parabola where it changes direction, lies on the line of symmetry, and EXACTLY halfway between the two x intercepts

Minimum

When a>0

Maximum

When a<0

Vertex form

y = a(x-h)²+k, where (h,k) is the vertex

h is subtracted from, and k is added.

When a is more than 0, vertex is a minimum

To find zeros

Complete the square and solve for x

To put standard ax²+bx+c = y into vertex form

Move the constant on the side of y, add (b/2)² to both sides, simplify y side and put the other side as a perfect square, then move the constant to the other side.

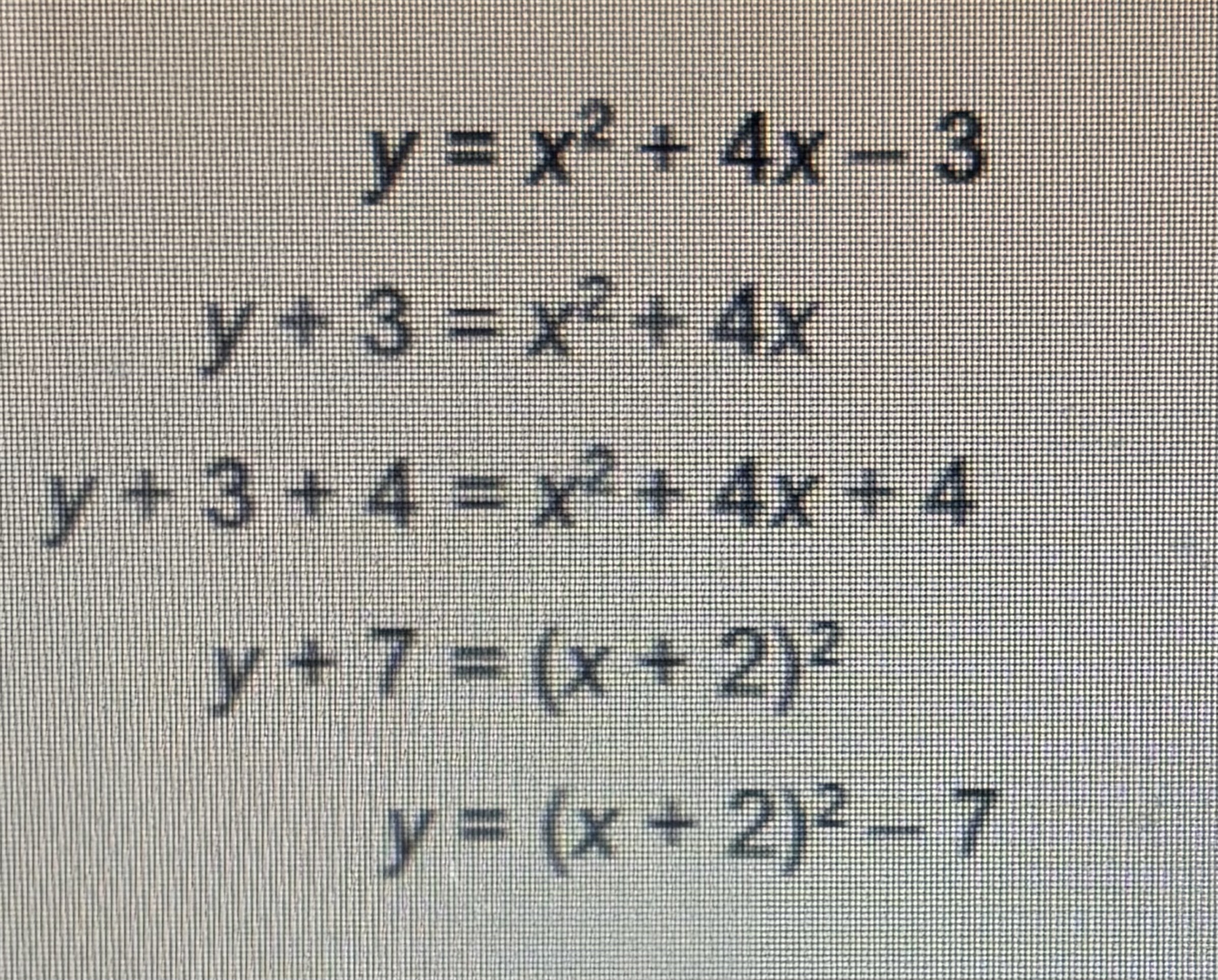
How to find line of symmetry

The line of symmetry is h in y=a(x-h)² + k

The quadratic formula

y = -b±the square root of b² - 4ac/ 2a

When solving the quadratic equations, solutions contain square roots/radicals that can sometimes be simplified

It’s either a perfect square, or can be simplified with the multiplication property of square roots, Some solutions are imaginary numbers

Radicals

Terms in the form of a “square root sign”

Discriminant

The number under the radical in the quadratic formula

b² - 4ac

Positive discriminant

2 solutions

Discriminant = 0

One solution

Negative discriminant

No real solutions