MATH 227 - 10.3 (Polar Coordinates)

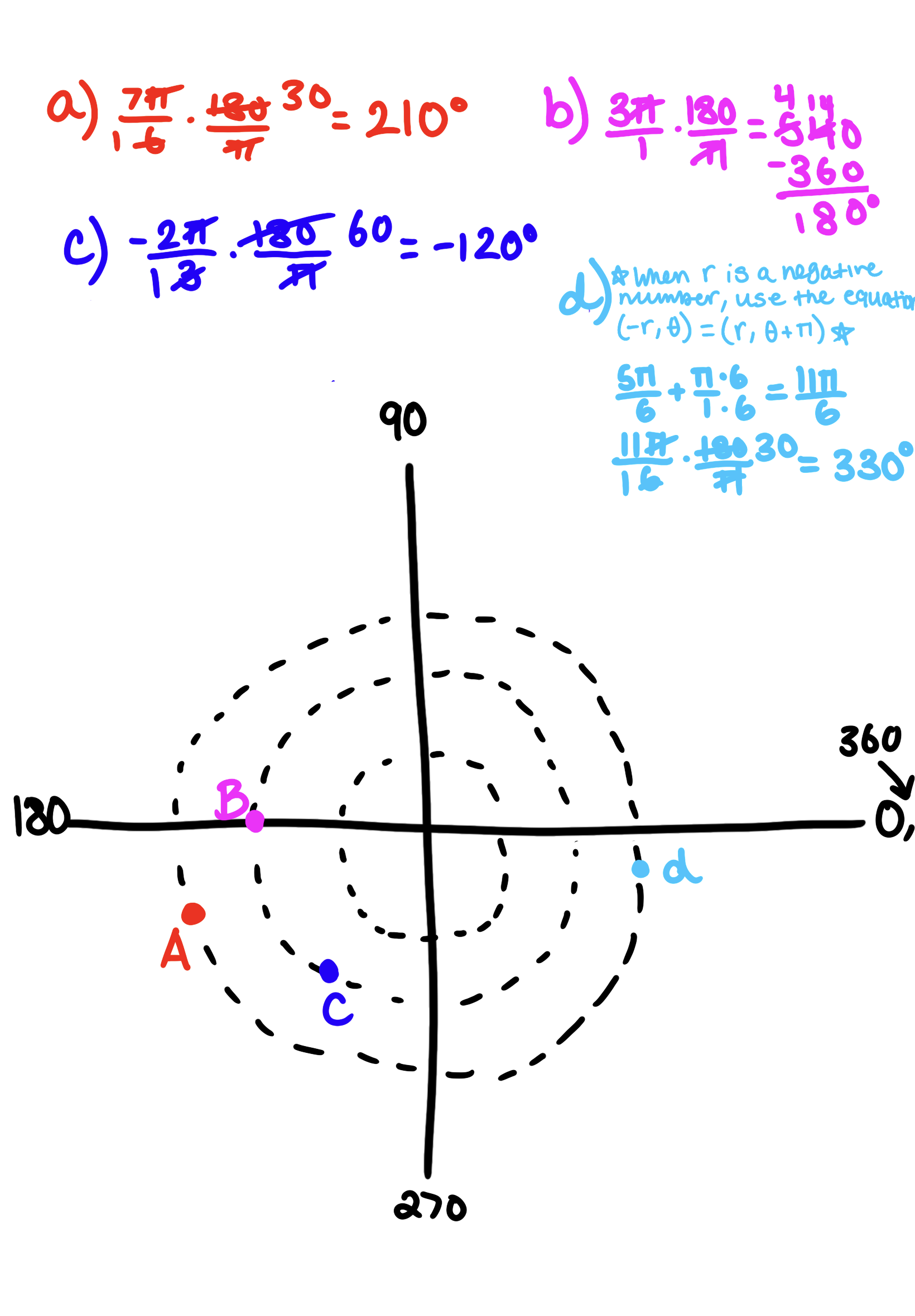
Plot the following polar points on the same graph:

a. (3, 7π/6)

b. (2, 3π)

c. (2, -2π/3)

d. (-3, 5π/6)

Convert the point (2, π/3) from Polar to Cartesian coordinates.

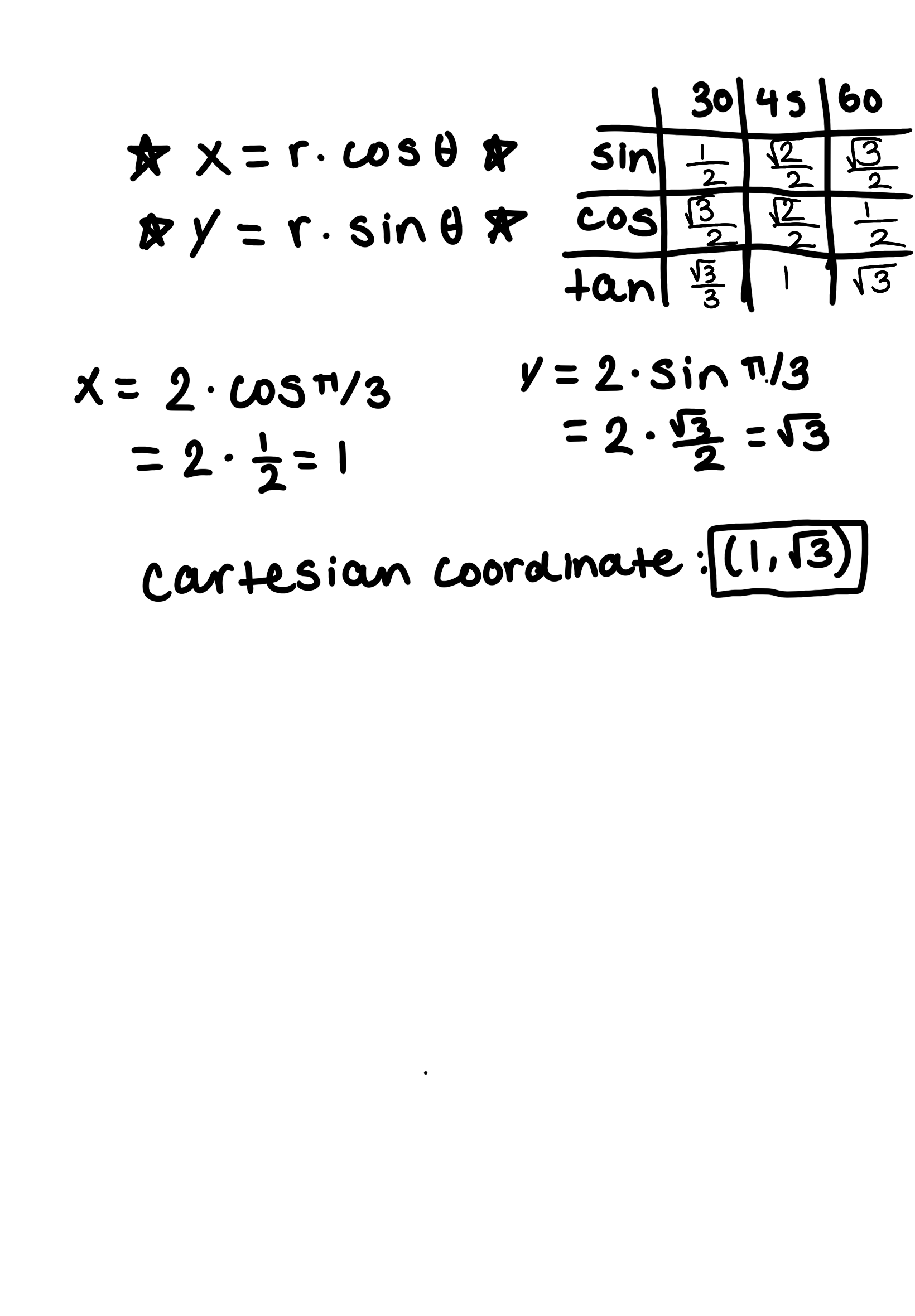
A. Convert the point (1,-1) from Cartesian to Polar coordinates using (r, 𝜃), one with 𝜃 > 0 and one with 𝜃 < 0

B. Plot the Polar coordinate on a graph

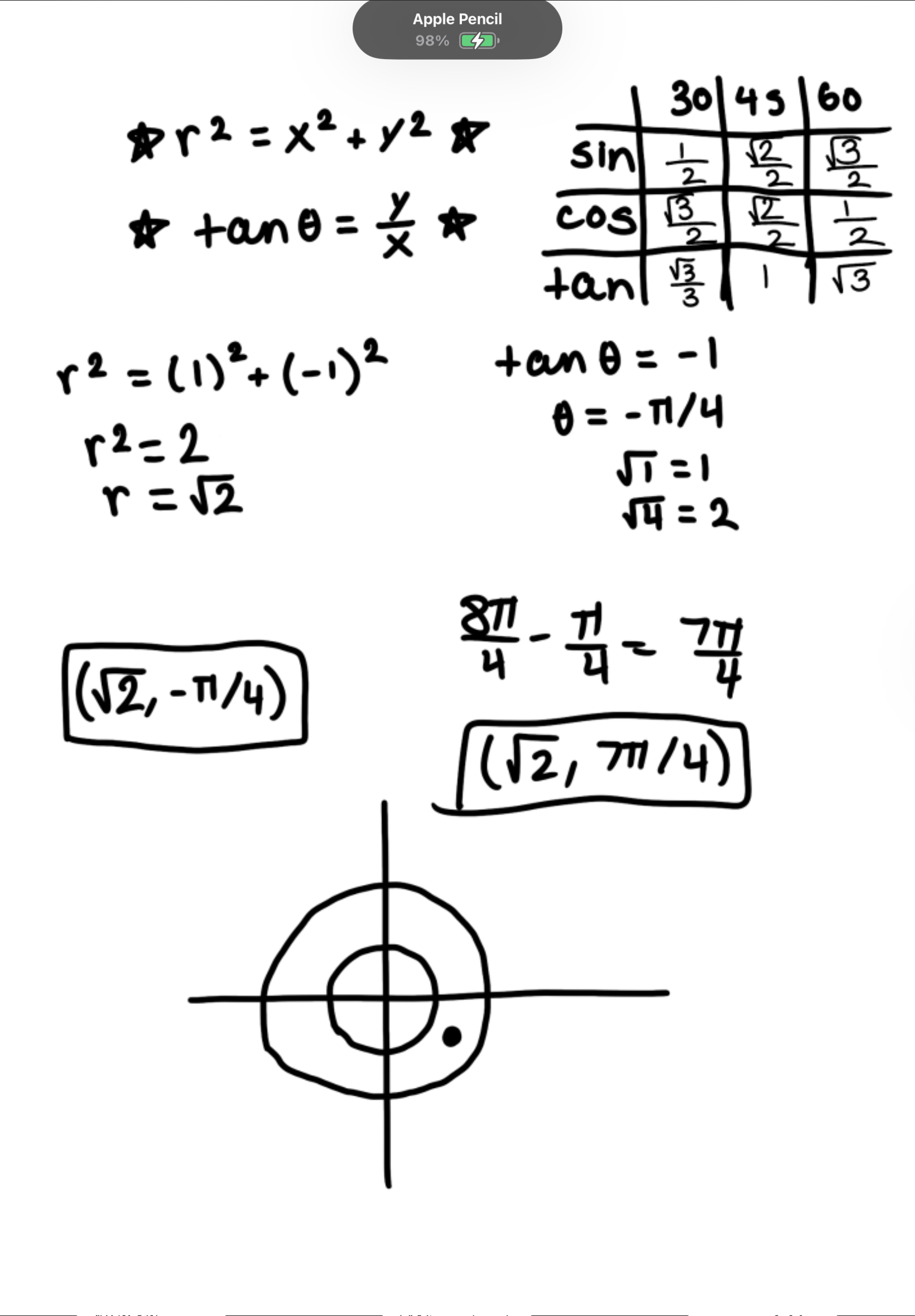
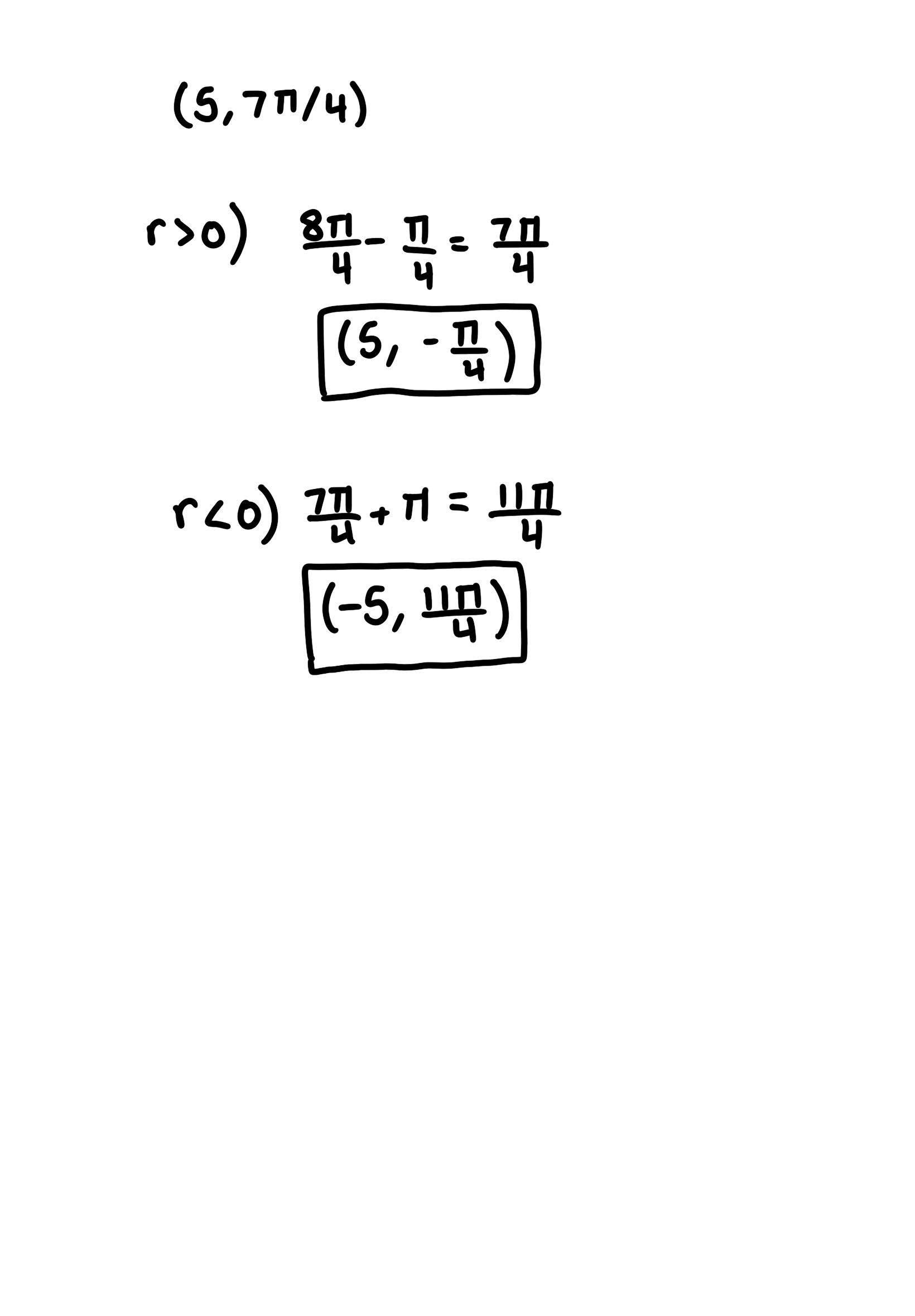
Find two other pairs of polar coordinates of the given polar coordinate (5, 7𝜋/4) using (r, 𝜃), one with r > 0 and one with r < 0

Find two other pairs of polar coordinates of the given polar coordinate (−6, 𝜋/3) using (r, 𝜃), one with r > 0 and one with r < 0

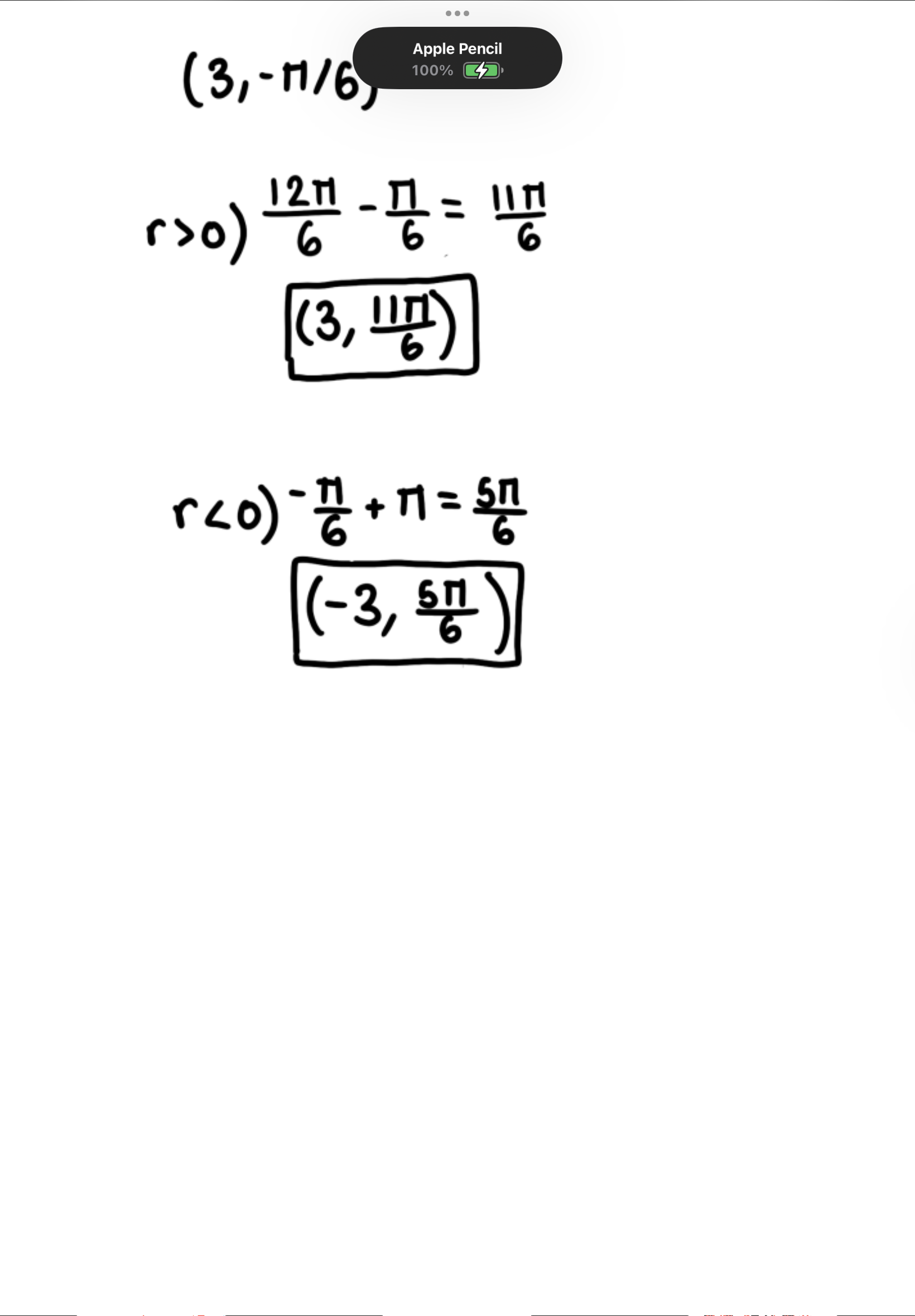
Find two other pairs of polar coordinates of the given polar coordinate (3, −𝜋/6) using (r, 𝜃), one with r > 0 and one with r < 0

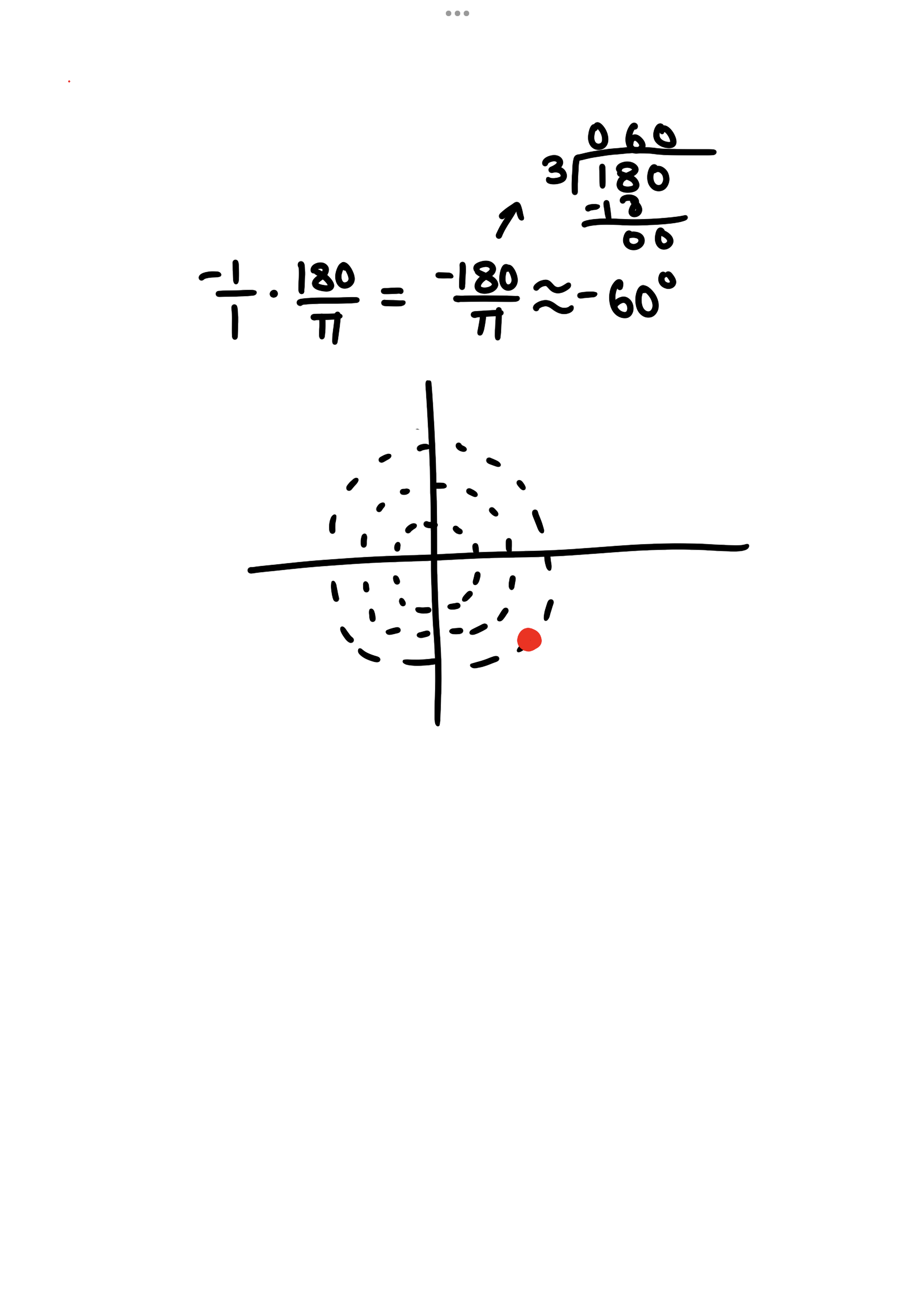
Plot the polar coordinate (3,-1)

The Cartesian coordinate of a point is given (5√3, 5)

1. Find polar coordinates (r, 𝜃) of the point, where r > 0 and 0 ≤ 𝜃 < 2𝜋.

2. Find polar coordinates (r, 𝜃) of the point, where r < 0 and 0 ≤ 𝜃 < 2𝜋.

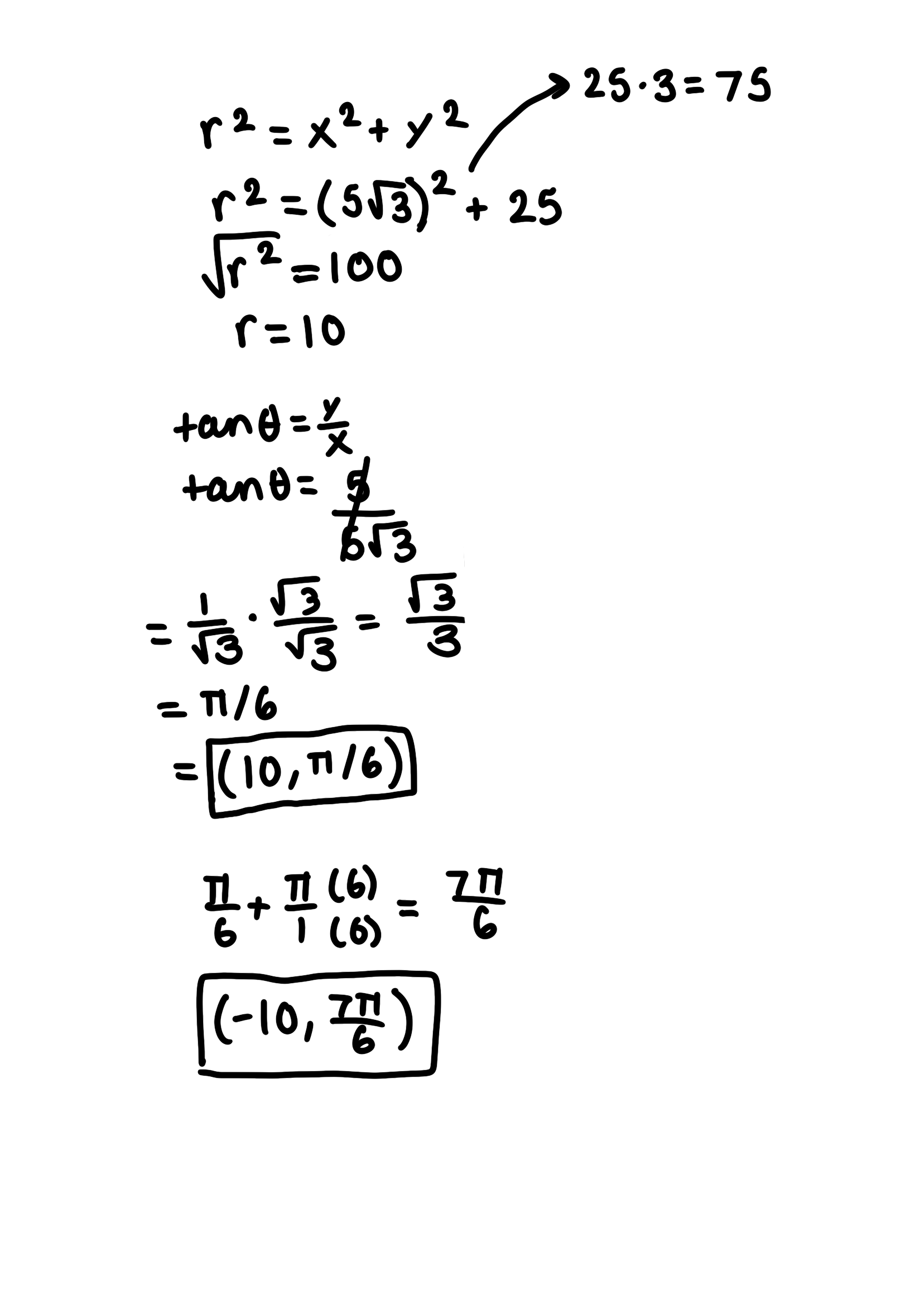
Find a cartesian equation for the polar curve r = 2cosθ

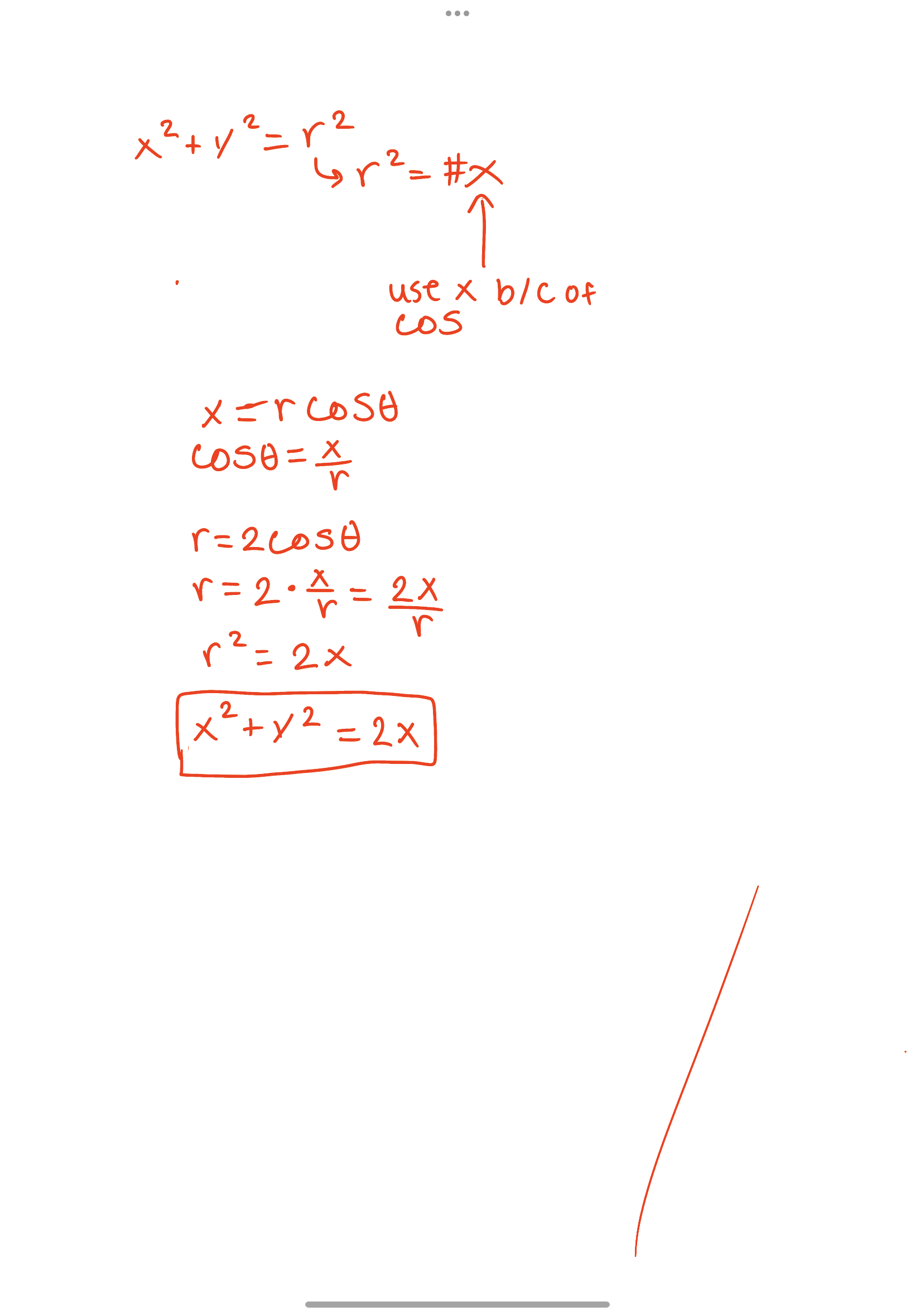
Find a cartesian equation for the polar curve r = 2sinθ

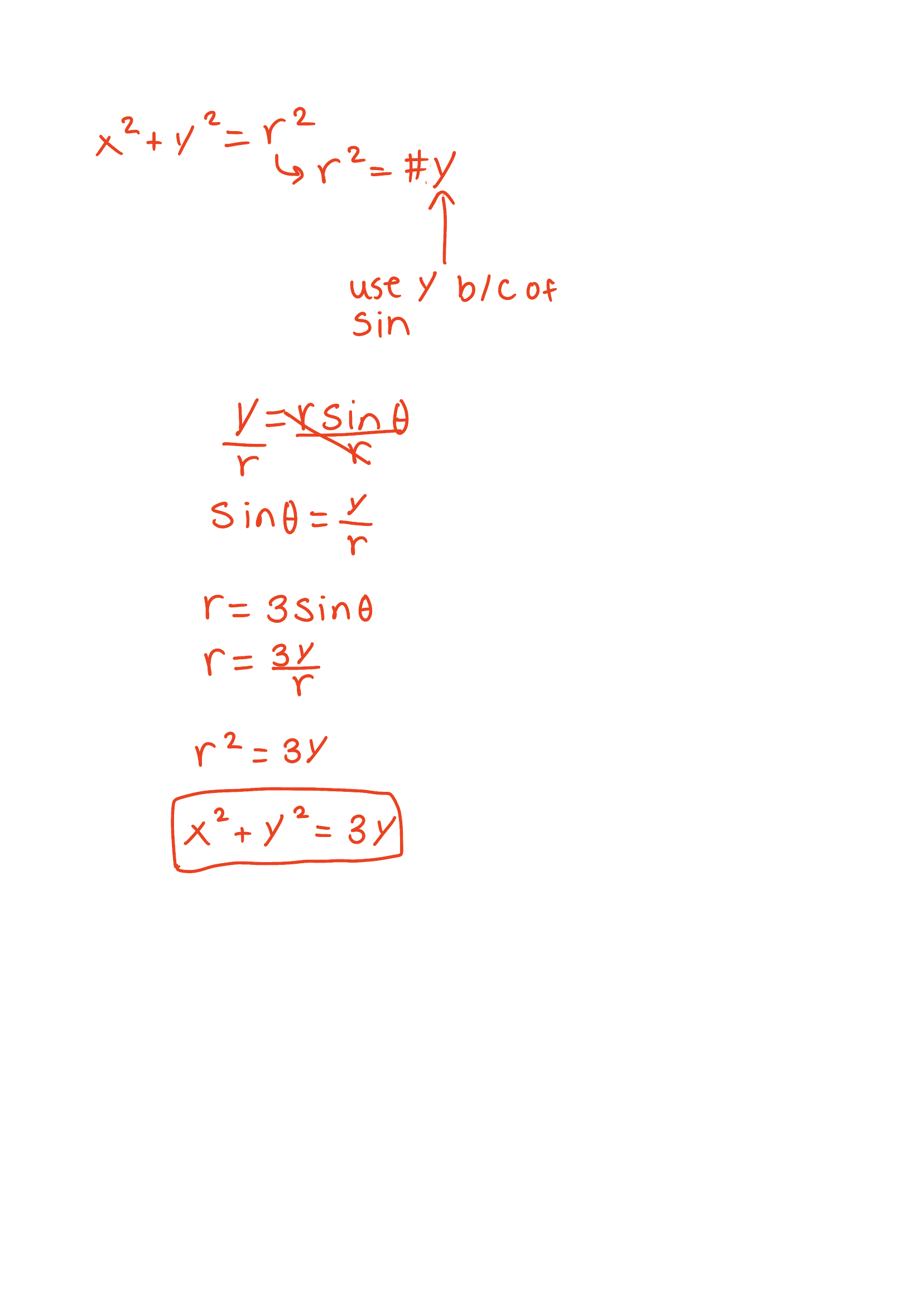
Sketch the curve r = 2cosθ, 0 ≤ 𝜃 < 2𝜋.

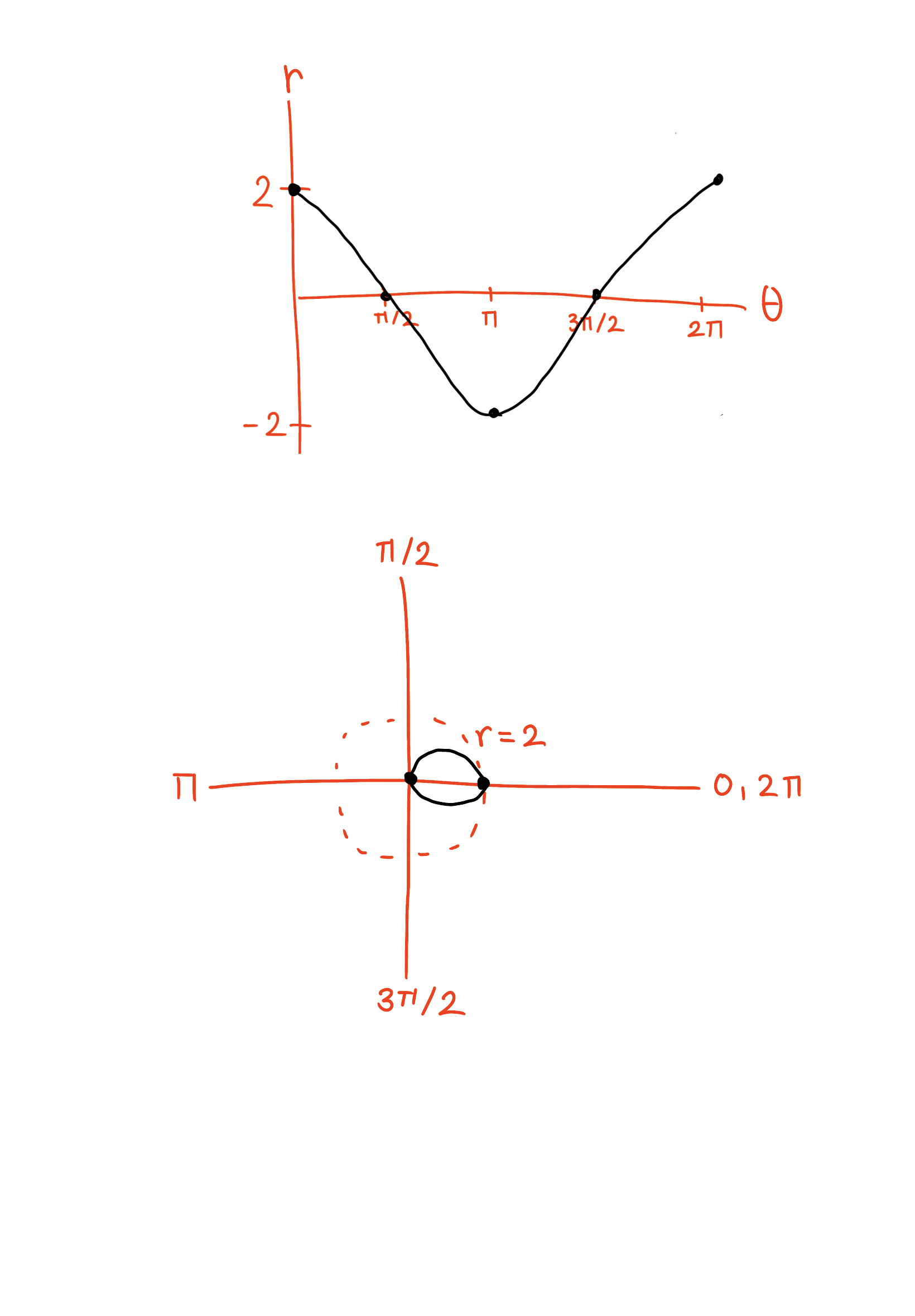
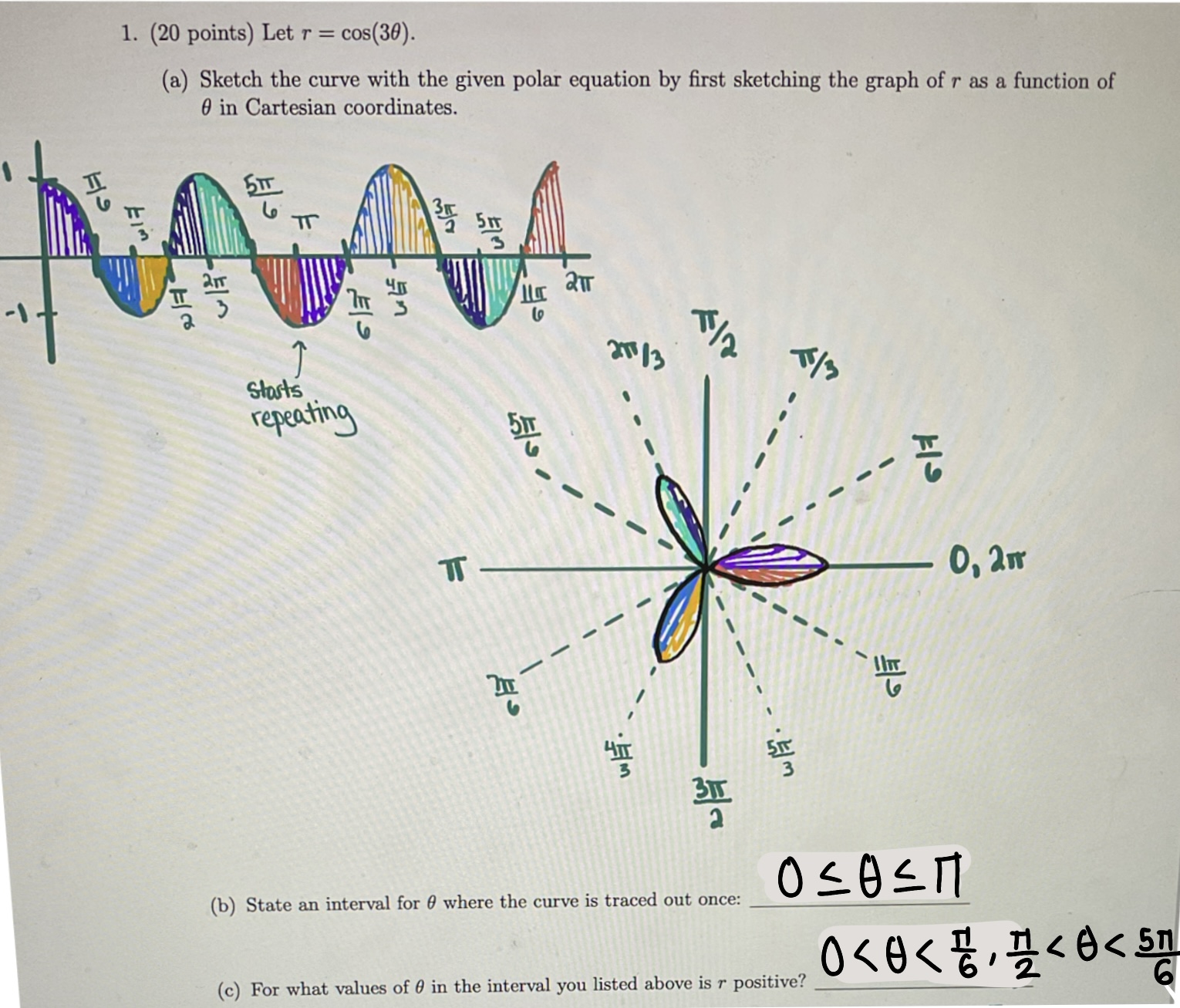
Sketch the curve r = cos(2θ), 0 ≤ 𝜃 < 2𝜋.

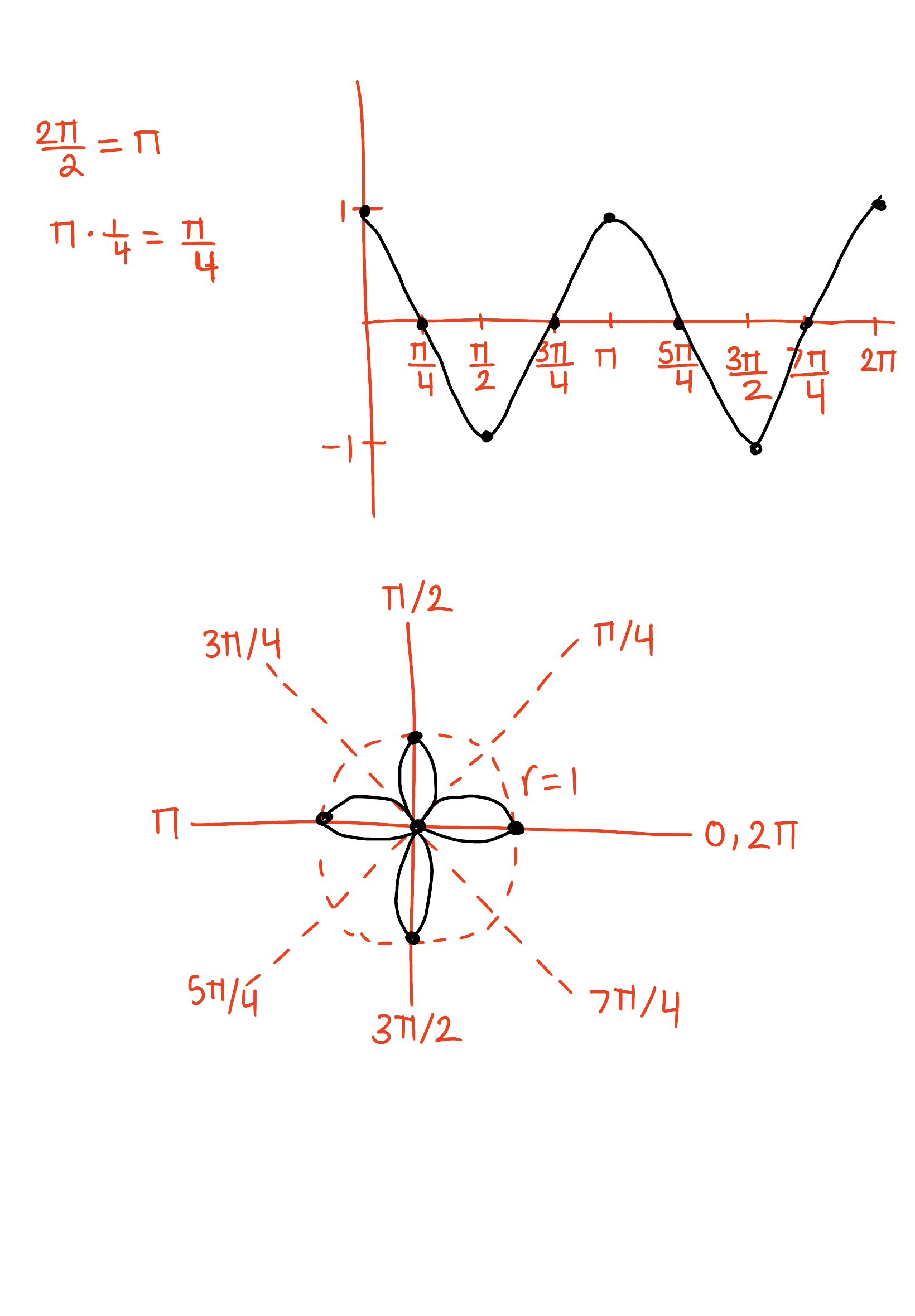
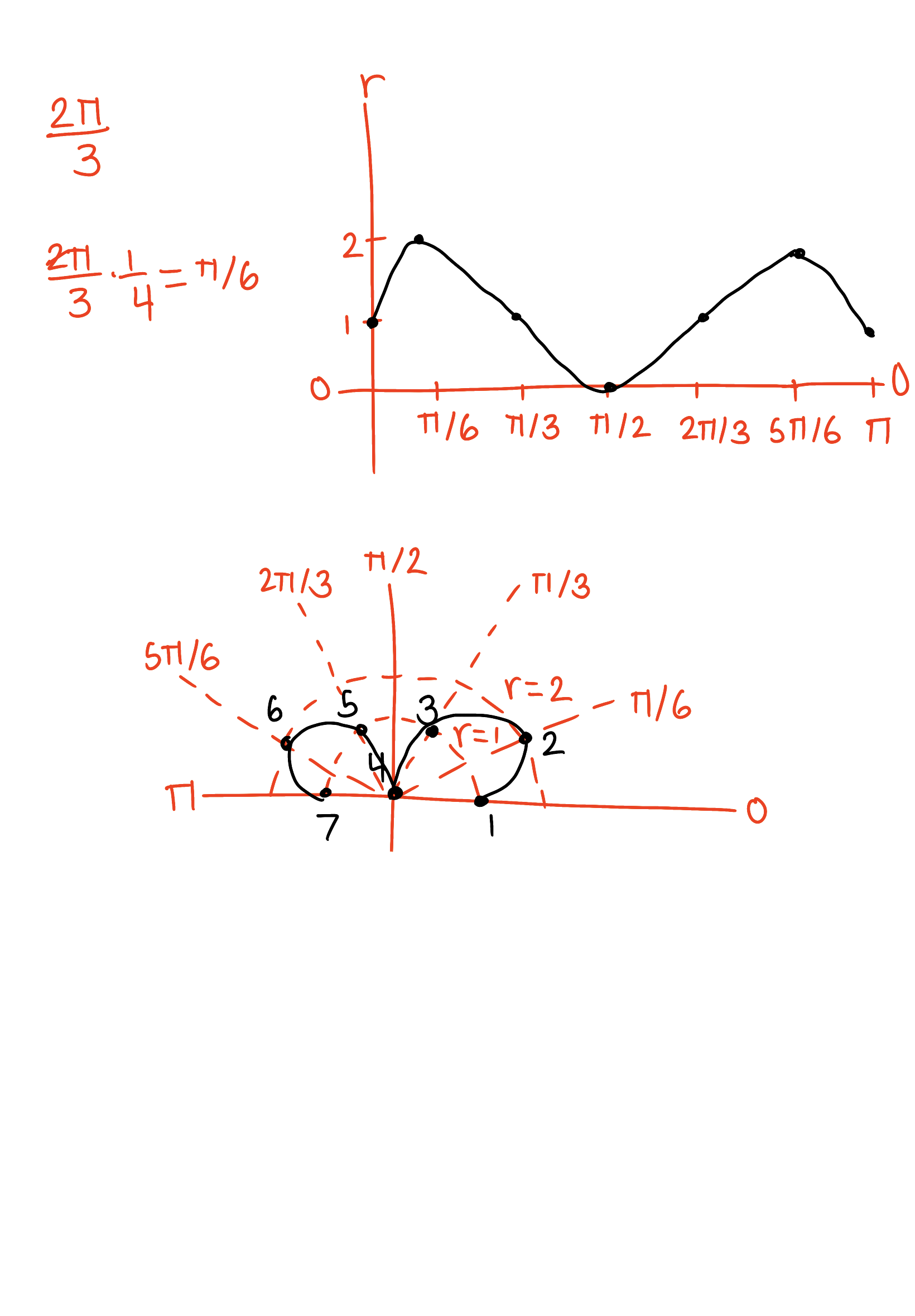
Sketch the curve r = 2sin(1/2θ) +1, 0 ≤ 𝜃 < 2𝜋.

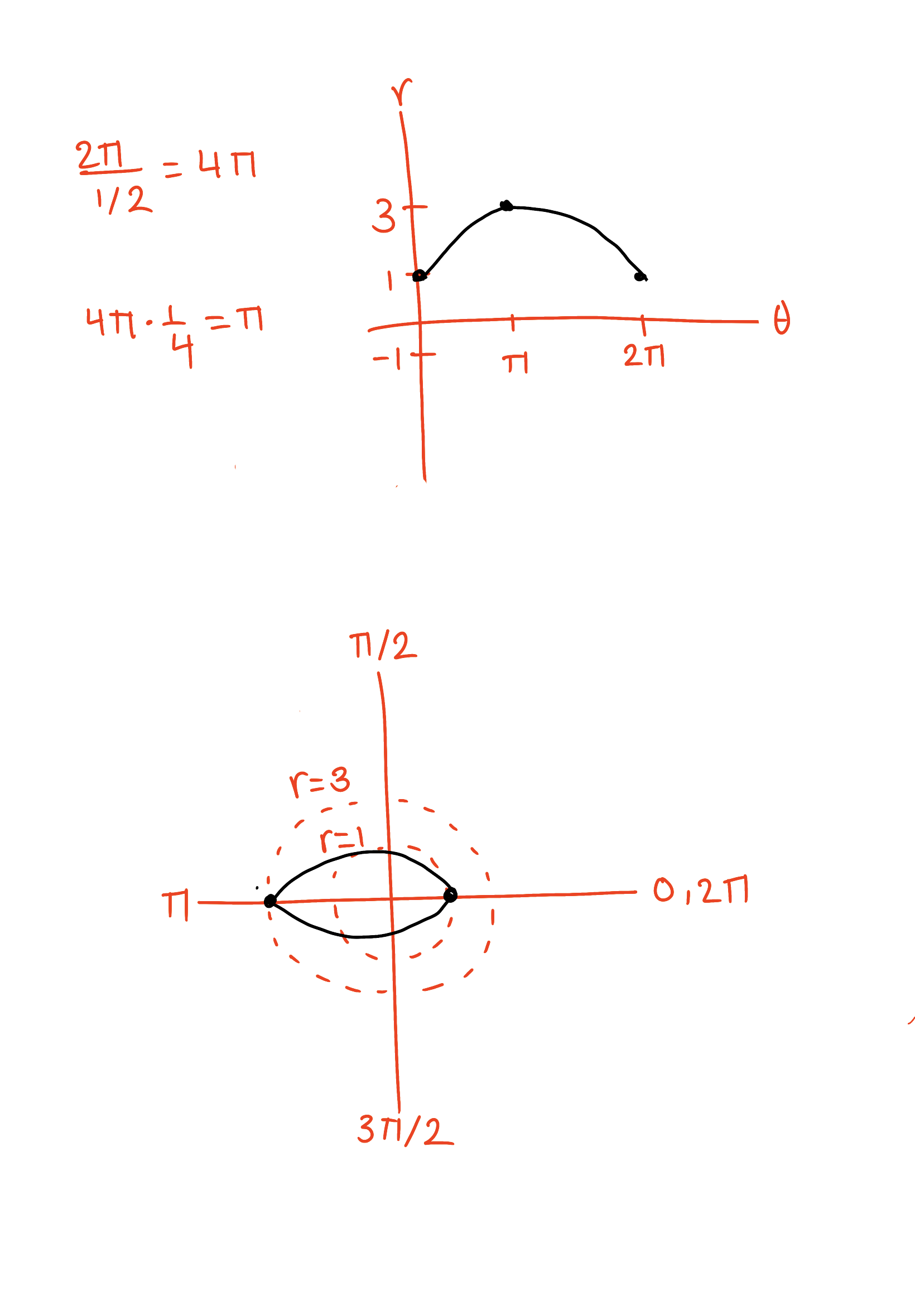
Sketch the curve r = sin(3θ) +1, 0 ≤ 𝜃 < 𝜋.