Momentum

Key Ideas

Impulse can be expressed both as force times a time interval and as a change in momentum.
The total momentum of a set of objects before a collision = the total momentum of a set of objects after a collision.
Momentum is a vector, so leftward momentum can “cancel out” rightward momentum.
If an object is moving, it has momentum.
Definition of momentum: It is equal to an object’s mass multiplied by that object’s velocity

Momentum and Impulse

Units of momentum: kg.m/s, same as N·s
Momentum is a vector quantity abbreviated with a p.
Impulse is an object’s change in momentum.
- It also is equal to the force acting on an object multiplied by the time interval over which that force was applied.

Example

A man jumps off the roof of a building, 3.0 m above the ground. His mass is 70 kg. He estimates (while in free fall) that if he lands stifflegged, it will take him 3 ms (milliseconds) to come to rest. However, if he bends his knees upon impact, it will take him 100 ms to come to rest. Which way will he choose to land, and why?

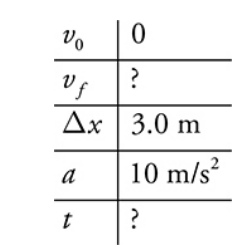
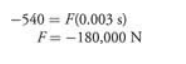
Calculus Version of the Impulse-Momentum Theorem

Impulse is a change in momentum.
When a force is changing with time:
\
When given the momentum of an object as a function of time, take the derivative to find the force on the object.
In a graph of momentum vs. time, the slope of the tangent to the graph gives the force at that point in time.
The area under that graph is impulse.

Conversation of Momentum

Momentum in an isolated system, where no net external forces act, is always conserved
When solving conversation of momentum questions, remember that momentum is a vector.

Example

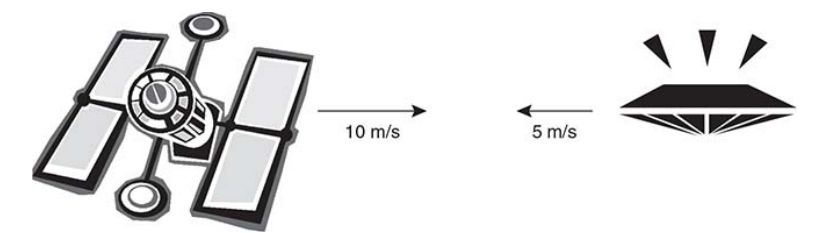
A satellite floating through space collides with a small UFO. Before the collision, the satellite was traveling at 10 m/s to the right, and the UFO was traveling at 5 m/s to the left. If the satellite’s mass is 70 kg, and the UFO’s mass is 50 kg, and assuming that the satellite and the UFO bounce off each other upon impact, what is the satellite’s final velocity if the UFO has a final velocity of 3 m/s to the right?

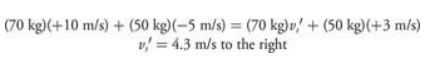
Motion of the Center of Mass

The center of mass of a system of objects obeys Newton’s second law
Example:
- An astronaut on a spacewalk throws a rope around a small asteroid and then pulls the asteroid toward him.
- The asteroid and the astronaut collide at the center of mass.
- Since no forces acted except due to the astronaut and asteroid, the center of mass must have no acceleration.
- The center of mass started at rest, and stays at rest, all the way until the objects collide.
- A toy rocket is in projectile motion so that it is on track to land 30 m from its launch point. While in the air, the rocket explodes into two identical pieces, one of which lands 35 m from the launch point. Where does the first piece land?
- Answer: 25 m from the launch point.
- Since the only external force acting on the rocket is gravity, the center of mass must stay in projectile motion and must land 30 m from the launch point.
- The two pieces are of equal mass, so if one is 5 m beyond the center of mass’s landing point, the other piece must be 5 m short of that point.

Finding the Center of Mass

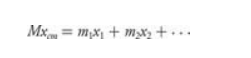
Multiply the mass of each object by its position, and divide by the total mass M to find the position of the center of mass.

Elastic and Inelastic Collisions

Elastic collision: A collision in which kinetic energy is conserved.
Inelastic Collision: A collision in which kinetic energy is not conserved.
Perfectly Inelastic Collision: A collision in which the two colliding objects stick together after impact.
Momentum is conserved even in a perfectly inelastic collision.

Two-Dimensional Collisions

To solve a two-dimensional collision problem, remember that momentum is a vector that can be broken into x and y components.
Momentum in the x-direction is always conserved.
Momentum in the y-direction is always conserved.

Note