Unit 1: Kinematics
1.1: Kinematics: Motion in One Dimension
- Kinematics is the study of motion without considering the forces that cause the motion.
- In one dimension, motion is described using distance, displacement, speed, velocity, and acceleration.
Distance and Displacement
- Distance: It is the total length of the path traveled by an object.
- Displacement: It is the change in position of an object from its initial position to its final position.
Speed and Velocity
- Speed: It is the rate at which an object covers distance.
- Velocity: It is the rate at which an object changes its displacement.
- Velocity is a vector quantity that has both magnitude and direction.
Acceleration
- Acceleration: It is the rate at which an object changes its velocity.
- Acceleration is a vector quantity that has both magnitude and direction.
- If an object is moving with a constant velocity, its acceleration is zero.
Equations of Motion
- The equations of motion describe the relationship between distance, displacement, speed, velocity, acceleration, and time.
- The equations of motion for an object moving with constant acceleration are:
v = u + at(velocity-time equation)s = ut + 1/2at^2(displacement-time equation)v^2 = u^2 + 2as(velocity-displacement equation)s = vt - 1/2at^2(displacement-velocity equation)- where u is the initial velocity, v is the final velocity, a is the acceleration, s is the displacement, and t is the time.
Vector Quantities
- A vector quantity is a physical quantity that has both magnitude and direction.
- It is represented by a directed line segment with an arrowhead, where the length of the line segment represents the magnitude of the vector and the direction of the arrowhead represents the direction of the vector.
- It can be represented by a boldface letter, such as v for velocity or F for force.
- A unit vector is a vector that has a magnitude of 1.
- Addition of Vectors:
- Vectors can be added using the head-to-tail method or the parallelogram method.
- The resultant vector is the vector that connects the tail of the first vector to the head of the last vector.
- Subtraction of Vectors:
- To subtract a vector, we add its negative vector.
- The negative vector has the same magnitude as the original vector but points in the opposite direction.
- Scalar Multiplication:
- A vector can be multiplied by a scalar (a real number).
- The magnitude of the vector is multiplied by the scalar, but the direction remains the same (unless the scalar is negative, in which case the direction is reversed).
Speed and Velocity
- Average speed is the ratio of the total distance traveled to the time required to cover that distance:
average speed = total distance / time
- Average velocity is defined as the change in position or displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs.
average velocity = displacement / time
- Speed and Velocity Sample Problem
An object’s position x, in meters, obeys the equation x = sin(t), where t is the time in seconds since the object began moving. How fast is the object moving at t = π/2 seconds?
- Solution
- This question asks for the velocity of the object at t = π/2 seconds.
- Since velocity is the time derivative of position, the velocity is given by
v = dsin(t) = cos(t).- Then plug in the value of t:
v(π/2) = cos(π/2) = 0 m/s.
Acceleration
Acceleration measures the rate-ofchange of an object’s velocity. An object’s average acceleration is defined as follows:
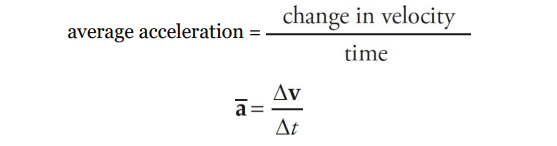
Acceleration Sample Problem
A car is traveling along a straight highway at a speed of 20 m/s. The driver steps on the gas pedal and, 3 seconds later, the car’s speed is 32 m/s. Find its average acceleration.
- Solution
- Here the direction does not change but the speed does, so there is a change in velocity.
- To obtain the average acceleration, simply divide the change in velocity,
32 m/s – 20 m/s = 12 m/s, by the time interval during which the change occurred:= ∆v/∆t = (12 m/s)/(3 s) = 4 m/s 2.
1.2 Kinematics: Motion in Two Dimensions
Position and Displacement
- Position: The location of an object in space, usually measured in meters (m).
- Displacement: The change in position of an object, usually measured in meters (m).
Velocity and Acceleration
- Velocity: The rate of change of an object's position, usually measured in meters per second (m/s).
- Acceleration: The rate of change of an object's velocity, usually measured in meters per second squared (m/s^2).
Projectile Motion
Projectile motion is the motion of an object that is launched into the air and then moves under the influence of gravity.
- Horizontal motion: The motion of the object in the x direction is constant and is not affected by gravity.
- Vertical motion: The motion of the object in the y direction is affected by gravity and follows a parabolic path.

Projectile Motion Sample Problems
- Example 1:
An object is projected upward with a 30° launch angle and an initial speed of 60 m/s. For how many seconds will it be in the air? How far will it travel horizontally before returning to its original height?
- Solution
- The total time the object spends in the air is equal to twice the time required to reach the top of the trajectory (because the parabola is symmetrical). So, as we did in the previous example, we find the time required to reach the top by setting vy equal to 0, and now double that amount of time:
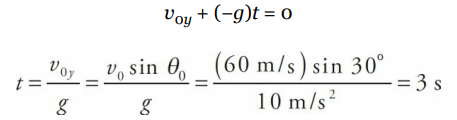
Therefore, the total flight time (that is, up and down) is
T = 2t = 2 × (3 s) = 6 s.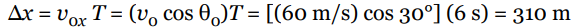
- Example 2:
An object is projected upward with a 30° launch angle and an initial speed of 40 m/s. How long will it take for the object to reach the top of its trajectory? How high is this?
- Solution
- When the projectile reaches the top of its trajectory, its velocity vector is momentarily horizontal; that is, vy = 0. We are asked how long it will take the object to reach this point with θ = 30 degrees. Using the vertical-motion equation for vy , we can set it equal to 0 and solve for t:
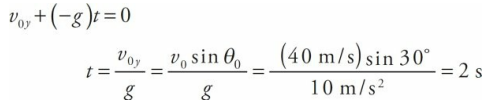
At this time, the projectile’s vertical displacement is
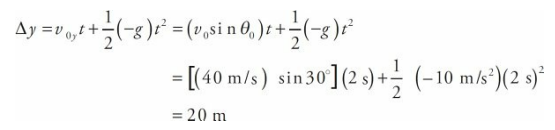
Free Fall
Free fall is a type of motion that occurs when an object falls under the influence of gravity alone, without any other forces acting upon it. In free fall, the object is said to be in a state of weightlessness, as it experiences zero apparent weight.
The acceleration experienced by an object in free fall is known as the acceleration due to gravity, denoted by the symbol 'g'. The value of 'g' is approximately 9.8 m/s^2 near the surface of the Earth, and is a constant value for all objects regardless of their mass.
The motion of an object in free fall can be described using the following equations of motion:
- Position: h = vi*t + (1/2)gt^2
- Velocity: v = vi + gt
- Acceleration: a = g
- where 'h' is the height of the object above the ground, 'vi' is the initial velocity of the object, 't' is the time elapsed, 'v' is the velocity of the object at time 't', and 'a' is the acceleration due to gravity.
In free fall, an object will continue to accelerate until it reaches its terminal velocity, which is the maximum velocity that the object can attain due to air resistance.
Once an object reaches its terminal velocity, it will continue to fall at a constant speed, as the upward force of air resistance balances the downward force of gravity.
Free Fall Sample Problem
A rock is dropped from an 80-meter cliff. How long does it take to reach the ground?
- Solution
- Since all of the rock’s motion is down, we call down the positive direction, so
a = +g. We’re given v0 , ∆y, and a, and we are asked for t. So v is missing; it isn’t given and it isn’t asked for, and we use Big Five #3:
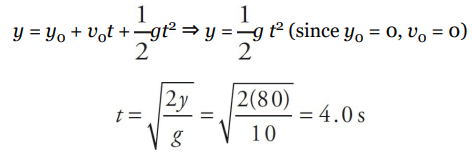
Kinematics with Graphs
Consider an object moving along a straight axis in such a way that its velocity, v, as a function of time, t, is given by the following velocity-vs.-time graph:
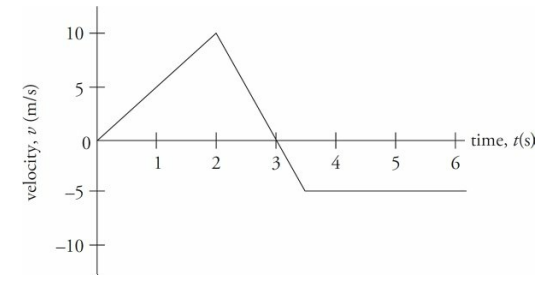
At time t = 0, the object’s velocity was v = 0. Over the first two seconds, its velocity increased steadily to 10 m/s. At time t = 2 s, the velocity then began to decrease (eventually becoming v = 0, at time t = 3 s). The velocity then became negative after t = 3 s, reaching v = –5 m/s at time t = 3.5 s. From t = 3.5 s on, the velocity remained a steady –5 m/s.
First, the fact that the velocity changed from t = 0 to t = 2 s tells us that the object accelerated. The acceleration during this time was
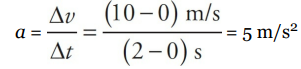
Note, however, that the ratio that defines the acceleration, ∆v/∆t, also defines the slope of the v-vs.-t graph. Therefore, “The slope of a velocity-vs.-time graph gives the average acceleration.“
What was the acceleration from time t = 2 s to time t = 3.5 s? The slope of the line segment joining the point (t, v) = (2 s, 10 m/s) to the point (t, v) = (3.5 s, –5 m/s) is
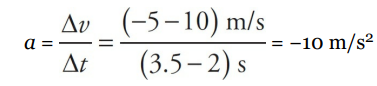
What is the object’s acceleration from time t = 3.5 s to time t = 6 s? Since the line segment from t = 3.5 s to t = 6 s is horizontal, its slope is zero, which indicates that the acceleration is zero, but you can also see this from looking at the graph; the object’s velocity did not change during this time interval.
Uniformly Accelerated Motion
- Uniformly accelerated motion is a type of motion where the acceleration of an object remains constant throughout its motion. This type of motion is characterized by the following equations:
v = u + at: This equation relates the final velocity (v) of an object to its initial velocity (u), acceleration (a), and time (t).s = ut + 1/2at^2: This equation relates the displacement (s) of an object to its initial velocity (u), acceleration (a), and time (t).v^2 = u^2 + 2as: This equation relates the final velocity (v) of an object to its initial velocity (u), acceleration (a), and displacement (s).
- Some key points to remember about uniformly accelerated motion are:
- The acceleration remains constant throughout the motion.
- The velocity of the object changes at a constant rate.
- The displacement of the object is directly proportional to the square of the time elapsed.
- Uniformly accelerated motion is commonly observed in free fall, where an object falls under the influence of gravity. In this case, the acceleration due to gravity is approximately constant and equal to 9.8 m/s^2.
The Big Five
- These five quantities are related by a group of five equations that we call the Big Five. They work in cases where acceleration is uniform, which are the ones we’re considering.
- Each of the Big Five equations is missing one of the five kinematic quantities.
- To decide which equation to use when solving a problem, determine which of the kinematic quantities is missing from the problem—that is, which quantity is neither given nor asked for—and then use the equation that doesn’t contain that variable.
| Equations | Missing Variable | |
|---|---|---|
| Big Five #1 | 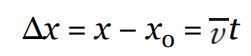 | a |
| Big Five #2 | 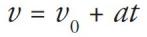 | ∆x |
| Big Five #3 | 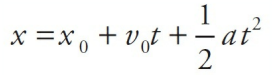 | v |
| Big Five #4 | 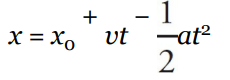 | v0 |
| Big Five #5 | 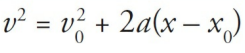 | t |