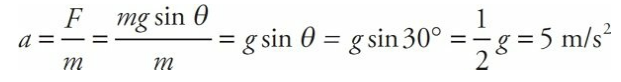Unit 2: Newton's Laws of Motion
2.1: Newton's Laws of Motion: First and Second Law
Newton's First Law of Motion
- Also known as the law of inertia
- States that an object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity, unless acted upon by an external force
- Inertia is the tendency of an object to resist changes in its motion
- The greater the mass of an object, the greater its inertia
- This law is important in understanding the behavior of objects in the absence of external forces, such as in space or in a vacuum
- It also explains why seat belts are important in cars, as they prevent passengers from continuing to move forward at the same speed when the car suddenly stops
- This law is the basis for the concept of momentum, which is the product of an object's mass and velocity
First Law Sample Problem
What net force is required to maintain a 5,000 kg object moving at a constant velocity of magnitude 7,500 m/s?
Solution
- The First Law says that any object will continue in its state of motion unless a force acts on it.
- Therefore, no net force is required to maintain a 5,000 kg object moving at a constant velocity of magnitude 7,500 m/s.
- Here’s another way to look at it: Constant velocity means a = 0, so the equation Fnet = ma immediately gives Fnet = 0.
Newton's Second Law of Motion
Newton's Second Law of Motion states that the acceleration of an object is directly proportional to the force applied to it and inversely proportional to its mass.
The formula for Newton's Second Law of Motion is F = ma, where F is the force applied, m is the mass of the object, and a is the acceleration produced.
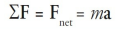
This law is also known as the law of acceleration.
The direction of the force applied determines the direction of the acceleration produced.
The greater the force applied, the greater the acceleration produced, and the greater the mass of the object, the smaller the acceleration produced.
This law is used to calculate the force required to move an object of a certain mass at a certain acceleration.
A force of 1 kg·m/s 2 is renamed 1 newton
Newton's Second Law of Motion is essential in understanding the behavior of objects in motion and is used in various fields such as engineering, physics, and sports.
Second Law Sample Problem
How much force is required to cause an object of mass 2 kg to have an acceleration of 4 m/s 2?
Solution
- According to the Second Law,
Fnet = ma = (2 kg)(4 m/s 2 ) = 8 N.
Friction Force
Friction force is a force that opposes motion between two surfaces that are in contact.
- It is caused by the irregularities in the surfaces that come into contact with each other.
- The force of friction acts parallel to the surfaces in contact and in the opposite direction to the direction of motion or the applied force.
There are three types of friction:
- Static Friction: It is the friction that exists between two surfaces that are not moving relative to each other. The static friction force is equal and opposite to the applied force until the applied force exceeds the maximum static friction force, after which the object starts moving.
- Kinetic Friction: It is the friction that exists between two surfaces that are moving relative to each other. The kinetic friction force is constant and is less than the maximum static friction force.
- Rolling Friction: It is the friction that exists between a rolling object and the surface it is rolling on. Rolling friction is less than static and kinetic friction.
The factors that affect friction are:
- Nature of the Surfaces: The nature of the surfaces in contact affects the friction force. Rough surfaces have more friction than smooth surfaces.
- Normal Force: The normal force is the force exerted by a surface perpendicular to the surface in contact. The friction force is directly proportional to the normal force.
- Surface Area: The surface area in contact affects the friction force. The larger the surface area in contact, the greater the friction force.
The strengths of these two types of friction forces are given by the following equations:
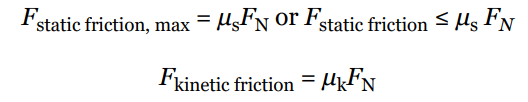
Weight
The weight of an object is the gravitational force exerted on it by a gravitational field.
Mass is an intrinsic property of an object that measures its inertia. An object’s mass does not change with location.
Since weight is a force, we can use F = ma to compute it, where the acceleration is the gravitational force imposed on an object. Therefore, setting a = g, the equation F = ma becomes
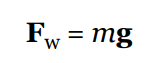
The Normal Force
- The component of the contact force that’s perpendicular to the surface is called the normal force on the object.
- The normal force comes from electrostatic interactions among atoms.
- The normal force is what prevents objects from falling through tabletops or you from falling through the floor.
- The normal force is denoted by FN, or simply by N.
2.2: Uniform Circular Motion
- Uniform circular motion is the motion of an object moving in a circular path at a constant speed. The direction of the velocity of the object is constantly changing, but the magnitude of the velocity remains constant.
- In order for an object to move in a circular path, there must be a force acting on it towards the center of the circle. This force is called the centripetal force. The magnitude of the centripetal force is given by the equation:
F = (mv^2)/r- where F is the centripetal force, m is the mass of the object, v is the speed of the object, and r is the radius of the circle.
- Centrifugal force is a fictitious force that appears to act on an object moving in a circular path. It is not a real force, but rather an apparent force that arises from the fact that the object is moving in a curved path. The centrifugal force is equal in magnitude and opposite in direction to the centripetal force.
The following diagrams show examples of a ball on a string traveling in a horizontal circle and a vertical circle.
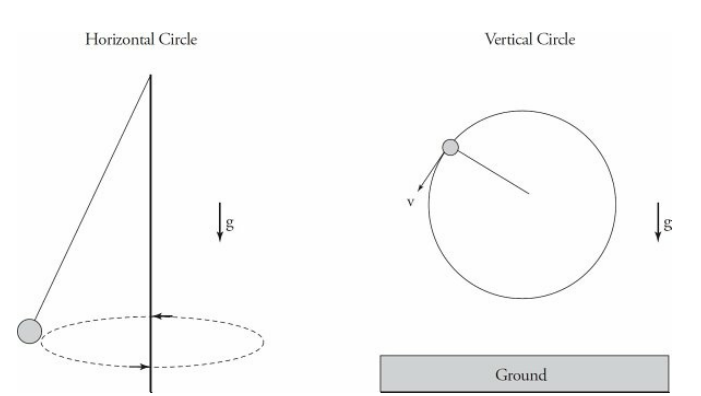
UCM Sample Problem
Example 1
An object of mass 5 kg moves at a constant speed of 6 m/s in a circular path of radius 2 m. Find the object’s acceleration and the net force responsible for its motion.
Solution
By definition, an object moving at constant speed in a circular path is undergoing uniform circular motion. Therefore, it experiences a centripetal acceleration of magnitude v 2/r, always directed toward the center of the circle:
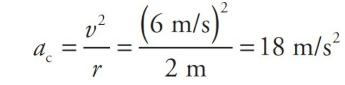
The force that produces the centripetal acceleration is given by Newton’s Second Law, coupled with the equation for centripetal acceleration:
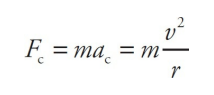
Example 2
A 10 kg mass is attached to a string that has a breaking strength of 200 N. If the mass is whirled in a horizontal circle of radius 80 cm, what maximum speed can it have? Assume the string is horizontal.
Solution
The first thing to do in problems like this is to identify what force(s) provide the centripetal force. In this example, the tension in the string (FT ) provides the centripetal force (Fc):
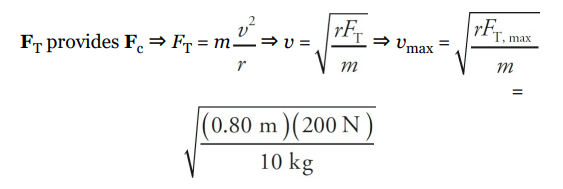
2.3: Newton's Third Law of Motion
- Newton's Third Law of Motion states that for every action, there is an equal and opposite reaction.
- This means that when an object exerts a force on another object, the second object exerts an equal and opposite force back on the first object.
- The forces are always of the same type, either both are attractive or both are repulsive.
- The Third Law applies to all types of forces, including gravitational, electromagnetic, and nuclear forces.
- The Third Law is important in understanding how objects move and interact with each other.
- It explains why rockets are able to launch into space and why cars are able to move forward.
- The Third Law also helps explain why collisions occur and how they affect the objects involved.
- It is important to note that the forces in the Third Law always act on different objects, not on the same object.
Pulleys
Pulleys are devices that change the direction of the tension force in the cords that slide over them.
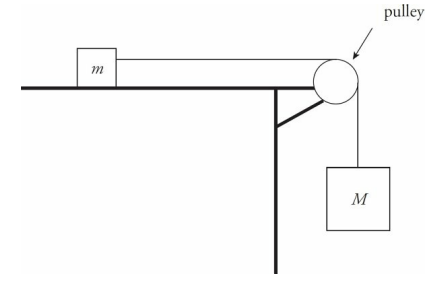
Pulley Sample Problem
In the diagram above, assume that the tabletop is frictionless. Determine the acceleration of the blocks once they’re released from rest.
Solution
There are two blocks, so draw two free-body diagrams: The positive directions for each block must coincide. If the block on the table travels to the right then the hanging block travels down. This is why down is positive for the hanging block.
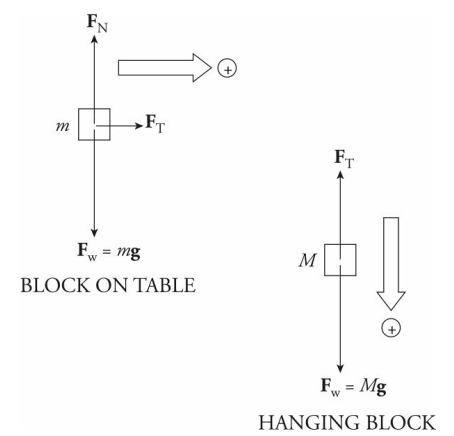
To get the acceleration of each one, we use Newton’s Second Law, Fnet = ma. Notice that while Fw = FN for the block on the table, Fw does not equal FT for the hanging block, because that block is in motion in the downward direction.
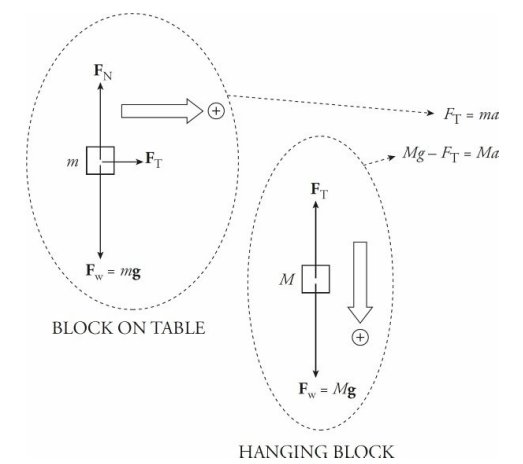
Note that there are two unknowns, FT and a, but we can eliminate FT by adding the two equations, and then we can solve for a.

Inclined Planes
An inclined plane is basically a ramp. If an object of mass m is on the ramp, then the force of gravity on the object, Fw = mg, has two components: One that’s parallel to the ramp (mg sin θ) and one that’s normal to the ramp (mg cos θ), where θ is the incline angle.
The force driving the block down the inclined plane is the component of the block’s weight that’s parallel to the ramp: mg sin θ.
When analyzing objects moving up or down inclined planes it is almost always easiest to rotate the coordinate axes such that the x-axis is parallel to the incline and the y-axis is perpendicular to the incline, as shown in the diagram.
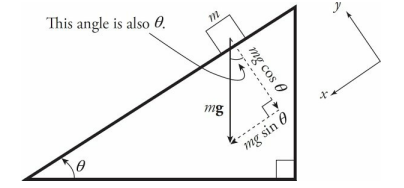
The object would accelerate in both the xand y-directions as it moved down along the incline if you did not rotate the axis. However, with the rotated axes, the acceleration in the y-direction is zero. Now we only have to worry about the acceleration in the x-direction.
Inclined Planes Sample Problem
A block slides down a frictionless inclined plane that makes a 30° angle with the horizontal. Find the acceleration of this block.
Solution
Let m denote the mass of the block, so the force that pulls the block down the incline is mg sin θ, and the block’s acceleration down the plane is