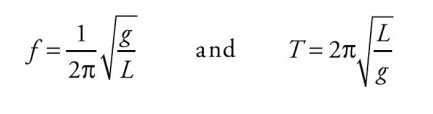Unit 6: Oscillations

6.1: Simple Harmonic Motion

• When a spring is compressed or stretched from its natural length, a force is created. If the spring is displaced by x from its natural length, the force it exerts in response is given by the equation

  

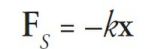
• This is known as Hooke’s law. The proportionality constant, k, is a positive number called the spring (or force) constant that indicates how stiff the spring is. The stiffer the spring, the greater the value of k. The minus sign in Hooke’s law tells us that FS and x always point in opposite directions.

Sample Problem (SHM)

A 12 cm-long spring has a force constant (k) of 400 N/m. How much force is required to stretch the spring to a length of 14 cm?

Solution

• The displacement of the spring has a magnitude of 14 – 12 = 2 cm = 0.02 m so, according to Hooke’s law, the spring exerts a force of magnitude F = –kx = –(400 N/m)(0.02 m) = –8 N. This is the restoring force, so we’d have to exert a force of 8 N to keep the spring in this stretched state.

\

6.2: Simple Harmonic Motion in Terms of Energy

• A stretched or compressed spring stores elastic potential energy, which is transformed into kinetic energy (and back again). This shuttling between potential and kinetic energy causes the oscillations. For a spring with spring constant k, the elastic potential energy it possesses—relative to its equilibrium position—is given by the equation

  

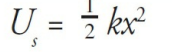
• In terms of energy transfers, we can describe the block’s oscillations as follows: When you initially pull the block out, you increase the elastic potential energy of the system. Upon releasing the block, this potential energy turns into kinetic energy, and the block moves.

  • As it passes through its equilibrium position, Us = 0. Then, as the block continues through that position, the spring is compressed, and the kinetic energy is transformed back into elastic potential energy.

• By Conservation of Mechanical Energy, the sum K + Us is a constant. Therefore, when the block reaches the maximum displacement, Us is maximized, so K must be minimized; in fact, K = 0 at the endpoints of the oscillation region. As the block is passing through equilibrium, x = 0, so Us = 0 and K is maximized.

  

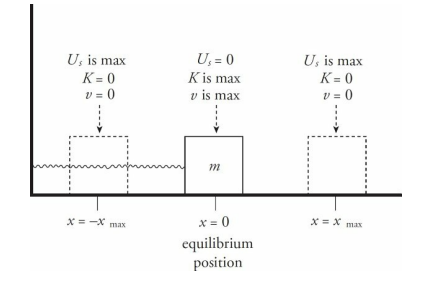
• The maximum displacement from equilibrium is called the amplitude of oscillation and is denoted by A. So instead of writing x = xmax , we write x = A.

Sample Problem

A block of mass m = 0.05 kg oscillates on a spring whose force constant k is 500 N/m. The amplitude of the oscillations is 4.0 cm. Calculate the maximum speed of the block.

Solution

• First, let’s get an expression for the maximum elastic potential energy of the system:

  

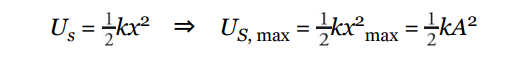
• When all this energy has been transformed into kinetic energy—which occurs at the equilibrium position—the block will have maximum kinetic energy and maximum speed

  

\

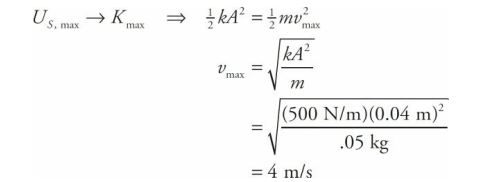
6.3: Kinematics of Simple Harmonic Motion

• As you watch the block oscillate, you should notice that it repeats each cycle of oscillation in the same amount of time.

  • A cycle is a roundtrip: for example, from position x = A over to x = –A and back again to x = A.
  • The amount of time it takes to complete a cycle is called the period of the oscillations, or T.
  • If T is short, the block is oscillating rapidly, and if T is long, the block is oscillating slowly.

• Another way of indicating the rapidity of the oscillations is to count the number of cycles that can be completed in a given time interval: the greater the number of completed cycles, the more rapid the oscillations.

  • The number of cycles that can be completed per unit time is called the frequency of the oscillations, or f, and is expressed in cycles per second.
  • One cycle per second is one hertz.

• One of the most basic equations of oscillatory motion expresses the inverse relationship between period and frequency:

  

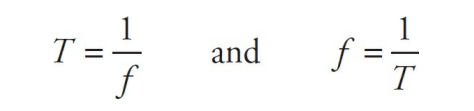
Sample Problem

A block oscillating on the end of a spring moves from its position of maximum spring stretch to maximum spring compression in 0.25 s. Determine the period and frequency of this motion.

Solution

• The period is defined as the time required for one full cycle.
• Moving from one end of the oscillation region to the other is only half a cycle.
• Therefore, if the block moves from its position of maximum spring stretch to maximum spring compression in 0.25 s, the time required for a full cycle is twice as much; T = 0.5 s.
• Because frequency is the reciprocal of period, the frequency of the oscillations is f = 1/T = 1/(0.5 s) = 2 Hz.

\

6.4: The Spring-Block Oscillator: Vertical Motion

• Consider a spring of negligible mass hanging from a stationary support. A block of mass m is attached to its end and allowed to come to rest, stretching the spring a distance d. At this point, the block is in equilibrium; the upward force of the spring is balanced by the downward force of gravity. Therefore,

  

  

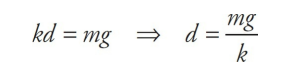
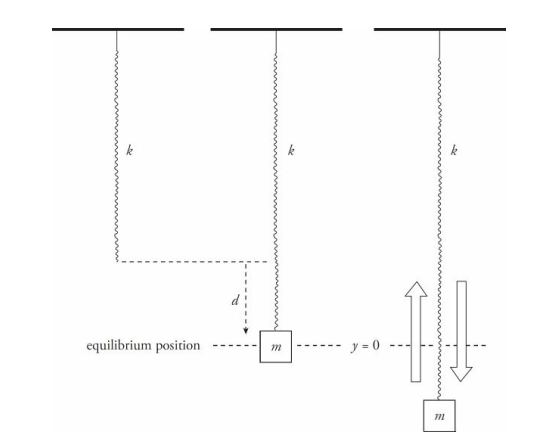
• Next, imagine that the block is pulled down a distance A and released.

  • The restoring force is greater than the block’s weight, and, as a result, the block accelerates upward.
  • As the block’s momentum carries it up through the equilibrium position, FS is less than the block’s weight.
  • As a result, the block decelerates, stops, and accelerates downward again, and the up-and-down motion repeats.

• When the block is at a distance y below its equilibrium position, the spring is stretched a total distance of d + y, so the upward spring force is equal to k(d + y).

  • The downward force stays the same, mg. The net force on the block is F = k(d + y) – mg
  • but this equation becomes F = ky, because kd = mg (as we saw above).

• Since the resulting force on the block, F = ky, has the form of Hooke’s law, we know that the vertical simple harmonic oscillations of the block have the same characteristics as the horizontal oscillations.

• The equilibrium position, y = 0, is not at the spring’s natural length, but at the point where the hanging block is in equilibium.

Sample Problem

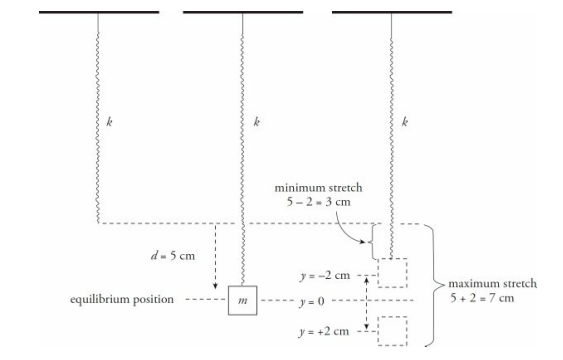
A block of mass m = 1.5 kg is attached to the end of a vertical spring of force constant k = 300 N/m. After the block comes to rest, it is pulled down a distance of 2.0 cm and released.

(a) What is the frequency of the resulting oscillations? (b) What are the minimum and maximum amounts of stretch of the spring during the oscillations of the block?

Solution

• The frequency is given by

  

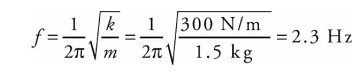
• Before the block is pulled down, to begin the oscillations, it stretches the spring by a distance

  

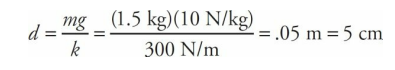
• Since the amplitude of the motion is 2 cm, the spring is stretched a maximum of 5 cm + 2 cm = 7 cm when the block is at the lowest position in its cycle, and a minimum of 5 cm – 2 cm = 3 cm when the block is at its highest position.

  

6.5: The Sinusoidal Description of SHM

• The position of the block during its oscillation can be written as a function of time. Take a look at the experimental setup below.

  

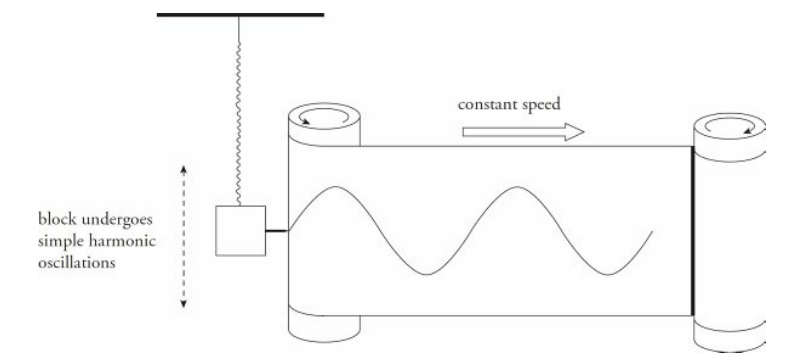
• A small pen is attached to the oscillating block, and it makes a mark on the paper as the paper is pulled along by the roller on the right. Clearly, the simple harmonic motion of the block is sinusoidal.

• The basic mathematical equation for describing simple harmonic motion is y = A sin (ωt)

  • where y is the position of the oscillator, A is the amplitude, ω is the angular frequency (defined as 2πf, where f is the frequency of the oscillations), and t is time.
  • Since sin(ωt) oscillates between –1 and +1, the quantity A sin(ωt) oscillates between –A and +A; this describes the oscillation region.

• If t = 0, then the quantity A sin (ωt) is also equal to zero. This means that y = 0 at time t = 0. However, what if y ≠ 0 at time t = 0? For example, if the oscillator is pulled to one of its amplitude positions, say y = A, and released at time t = 0, then y = A at t = 0.

• To account for the fact that the oscillator can begin anywhere in the oscillation region, the basic equation for the position of the oscillator given above is generalized as follows: y = A sin (ωt + ϕ0 )

  • where ϕ0 is called the initial phase. The argument of the sine function, ωt + ϕ0 , is called the phase (or phase angle).

  • By carefully choosing ϕ0 , we can be sure that the equation correctly specifies the oscillator’s position no matter where it may have been at time t = 0. The value of ϕ0 can be calculated from the equation

    

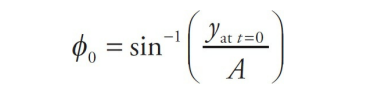
Sample Problem

A simple harmonic oscillator has an amplitude of 3.0 cm and a frequency of 4.0 Hz. At time t = 0, its position is y = 3.0 cm. Where is it at time t = 0.3 s?

Solution

• First, A = 3 cm and ω = 2πf = 2π(4.0 s^−1) = 8π s^−1 . The value of the initial phase is

  

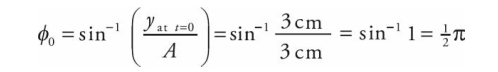
• Therefore, the position of the oscillator at any time t is given by the equation

  

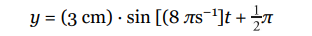
• So, at time t = 0.3 s, we find that y = (3 cm) · sin [(8 πs −1) (0.3 s) + π] = 0.93.

\

Instantaneous Velocity and Acceleration

• If the position of a simple harmonic oscillator is given by the equation y = A sin (ω t + ϕ0 ), its velocity and acceleration can be found by differentiation:

  

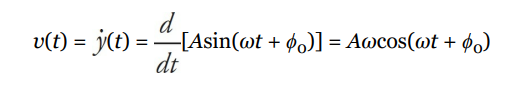
  • and

    

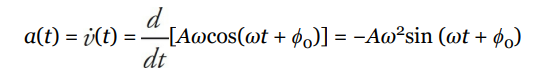
• Note that both the velocity and acceleration vary with time

\

6.6: Pendula

• A simple pendulum consists of a weight of mass m attached to a massless rod that swings, without friction, about the vertical equilibrium position.

• The restoring force is provided by gravity and, as the figure below shows, the magnitude of the restoring force when the bob is θ to an angle to the vertical is given by the equation:

  

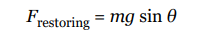
• Although the displacement of the pendulum is measured by the angle that it makes with the vertical, rather than by its linear distance from the equilibrium position (as was the case for the spring–block oscillator), the simple pendulum shares many of the important features of the spring–block oscillator.

  

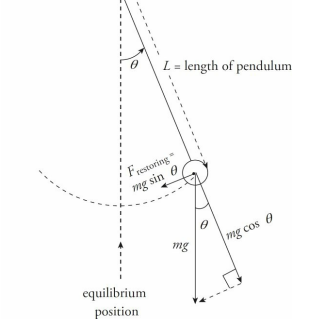
• Displacement is zero at the equilibrium position.

• At the endpoints of the oscillation region (where θ = ±θmax ), the restoring force and the tangential acceleration (at) have their greatest magnitudes, the speed of the pendulum is zero, and the potential energy is maximized.

• As the pendulum passes through the equilibrium position, its kinetic energy and speed are maximized.

  

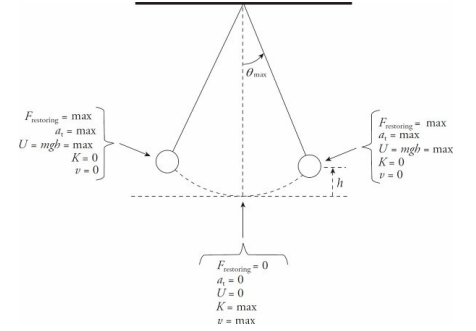
• Despite these similarities, there is one important difference. Simple harmonic motion results from a restoring force that has a strength that’s proportional to the displacement. The magnitude of the restoring force on a pendulum is mg sin θ, which is not proportional to the displacement θ. Strictly speaking, then, the motion of a simple pendulum is not really simple harmonic.

  • However, if θ is small, then sin θ ≈ θ (measured in radians). So, in this case, the magnitude of the restoring force is approximately mgθ, which is proportional to θ. So if θmax is small, the motion can be treated as simple harmonic.

• If the restoring force is given by mgθ, rather than mg sin θ, then the frequency and period of the oscillations depend only on the length of the pendulum and the value of the gravitational acceleration, according to the following equations:

  

\
\