Unit 7: Gravitation

Kepler’s First Law: Every planet moves in an elliptical orbit, with the Sun at one focus.
Kepler’s Second Law: As a planet moves in its orbit, a line drawn from the Sun to the planet sweeps out equal areas in equal time intervals.
Kepler’s Third Law: If T is the period, the time required to make one revolution, and a is the length of the semimajor axis of a planet’s orbit, then the ratio T^2/a^3 is the same for all planets orbiting the same star.

Proposed by Sir Isaac Newton in 1687
Describes the force of gravity between two objects
States that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them
Mathematically represented as F = G * (m1 * m2) / r^2, where F is the force of attraction, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between them
The gravitational constant, G, is a fundamental constant of nature and has a value of approximately 6.674 x 10^-11 N * m^2 / kg^2
Newton's Law of Gravitation is applicable to all objects in the universe, from the smallest particles to the largest celestial bodies
It is the basis for understanding the motion of planets, stars, and galaxies
It was later refined by Albert Einstein's theory of general relativity, which describes gravity as the curvature of spacetime caused by the presence of mass and energy.

Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field. It is defined as the work done in moving an object from infinity to a point in the gravitational field.
The formula for gravitational potential energy is:
- PE = mgh
- where PE is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above a reference point.
The units of gravitational potential energy are joules (J) in the SI system.
Gravitational potential energy is an important concept in physics as it helps to explain the behavior of objects in a gravitational field. It is also used in many practical applications, such as in the design of roller coasters and other amusement park rides.
Gravitational potential energy is a form of potential energy, which means that it can be converted into other forms of energy, such as kinetic energy. The total energy of a system, however, remains constant, according to the law of conservation of energy.

Kepler’s First Law states that the planets’ orbits are ellipses, but the ellipses that the planets in our solar system travel are nearly circular. The deviation of an ellipse from a perfect circle is measured by a parameter called its eccentricity.
The eccentricity, e, is the ratio of c (the distance between the center and either focus) to a, the length of the semimajor axis.
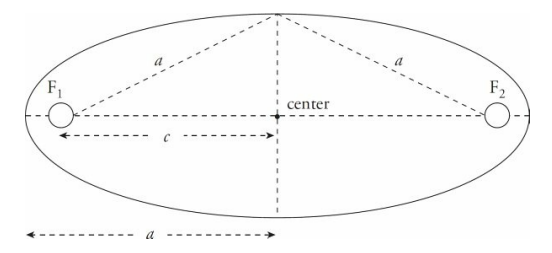
Kepler’s First Law also states that one of the foci of a planet’s elliptical orbit is located at the position of the Sun. Actually, the focus is at the center of mass of the Sun-planet system, because when one body orbits another, both bodies orbit around their center of mass, a point called the barycenter.
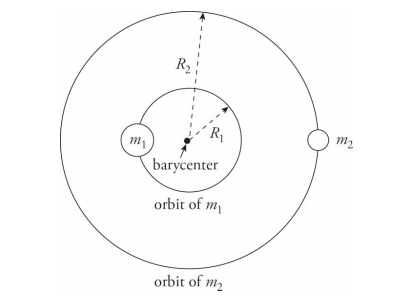
For most of the planets, which are much less massive than the Sun, this correction to Kepler’s First Law has little significance, because the center of mass of the Sun and the planet system is close enough to the Sun’s center.
For example, let’s figure out the center of mass of the Sun-Earth system.
- The mass of Earth is m = 5.98 × 10^24 kg, the mass of the Sun is M = 1.99 × 10^30 kg, and the Sun-Earth distance averages R = 1.496 × 10^11 m.
- Therefore, letting x = 0 be at the Sun’s center, we have