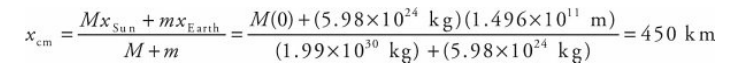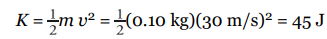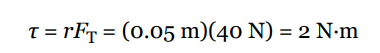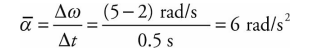AP Physics C: Mechanics Ultimate Guide
Unit 1: Kinematics
1.1: Kinematics: Motion in One Dimension
- Kinematics is the study of motion without considering the forces that cause the motion.
- In one dimension, motion is described using distance, displacement, speed, velocity, and acceleration.
Distance and Displacement
- Distance: It is the total length of the path traveled by an object.
- Displacement: It is the change in position of an object from its initial position to its final position.
Speed and Velocity
- Speed: It is the rate at which an object covers distance.
- Velocity: It is the rate at which an object changes its displacement.
- Velocity is a vector quantity that has both magnitude and direction.
Acceleration
- Acceleration: It is the rate at which an object changes its velocity.
- Acceleration is a vector quantity that has both magnitude and direction.
- If an object is moving with a constant velocity, its acceleration is zero.
Equations of Motion
- The equations of motion describe the relationship between distance, displacement, speed, velocity, acceleration, and time.
- The equations of motion for an object moving with constant acceleration are:
v = u + at(velocity-time equation)s = ut + 1/2at^2(displacement-time equation)v^2 = u^2 + 2as(velocity-displacement equation)s = vt - 1/2at^2(displacement-velocity equation)- where u is the initial velocity, v is the final velocity, a is the acceleration, s is the displacement, and t is the time.
Vector Quantities
- A vector quantity is a physical quantity that has both magnitude and direction.
- It is represented by a directed line segment with an arrowhead, where the length of the line segment represents the magnitude of the vector and the direction of the arrowhead represents the direction of the vector.
- It can be represented by a boldface letter, such as v for velocity or F for force.
- A unit vector is a vector that has a magnitude of 1.
- Addition of Vectors:
- Vectors can be added using the head-to-tail method or the parallelogram method.
- The resultant vector is the vector that connects the tail of the first vector to the head of the last vector.
- Subtraction of Vectors:
- To subtract a vector, we add its negative vector.
- The negative vector has the same magnitude as the original vector but points in the opposite direction.
- Scalar Multiplication:
- A vector can be multiplied by a scalar (a real number).
- The magnitude of the vector is multiplied by the scalar, but the direction remains the same (unless the scalar is negative, in which case the direction is reversed).
Speed and Velocity
- Average speed is the ratio of the total distance traveled to the time required to cover that distance:
average speed = total distance / time
- Average velocity is defined as the change in position or displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs.
average velocity = displacement / time
- Speed and Velocity Sample Problem
An object’s position x, in meters, obeys the equation x = sin(t), where t is the time in seconds since the object began moving. How fast is the object moving at t = π/2 seconds?
- Solution
- This question asks for the velocity of the object at t = π/2 seconds.
- Since velocity is the time derivative of position, the velocity is given by
v = dsin(t) = cos(t).- Then plug in the value of t:
v(π/2) = cos(π/2) = 0 m/s.
Acceleration
Acceleration measures the rate-ofchange of an object’s velocity. An object’s average acceleration is defined as follows:
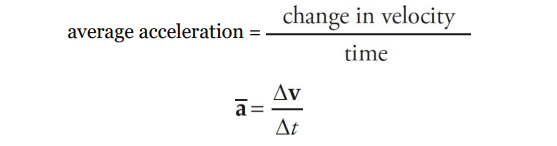
Acceleration Sample Problem
A car is traveling along a straight highway at a speed of 20 m/s. The driver steps on the gas pedal and, 3 seconds later, the car’s speed is 32 m/s. Find its average acceleration.
- Solution
- Here the direction does not change but the speed does, so there is a change in velocity.
- To obtain the average acceleration, simply divide the change in velocity,
32 m/s – 20 m/s = 12 m/s, by the time interval during which the change occurred:= ∆v/∆t = (12 m/s)/(3 s) = 4 m/s 2.
1.2 Kinematics: Motion in Two Dimensions
Position and Displacement
- Position: The location of an object in space, usually measured in meters (m).
- Displacement: The change in position of an object, usually measured in meters (m).
Velocity and Acceleration
- Velocity: The rate of change of an object's position, usually measured in meters per second (m/s).
- Acceleration: The rate of change of an object's velocity, usually measured in meters per second squared (m/s^2).
Projectile Motion
Projectile motion is the motion of an object that is launched into the air and then moves under the influence of gravity.
- Horizontal motion: The motion of the object in the x direction is constant and is not affected by gravity.
- Vertical motion: The motion of the object in the y direction is affected by gravity and follows a parabolic path.

Projectile Motion Sample Problems
- Example 1:
An object is projected upward with a 30° launch angle and an initial speed of 60 m/s. For how many seconds will it be in the air? How far will it travel horizontally before returning to its original height?
- Solution
- The total time the object spends in the air is equal to twice the time required to reach the top of the trajectory (because the parabola is symmetrical). So, as we did in the previous example, we find the time required to reach the top by setting vy equal to 0, and now double that amount of time:
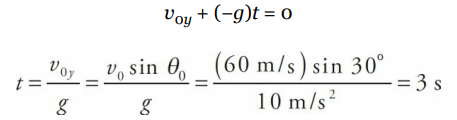
Therefore, the total flight time (that is, up and down) is
T = 2t = 2 × (3 s) = 6 s.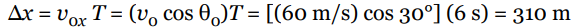
- Example 2:
An object is projected upward with a 30° launch angle and an initial speed of 40 m/s. How long will it take for the object to reach the top of its trajectory? How high is this?
- Solution
- When the projectile reaches the top of its trajectory, its velocity vector is momentarily horizontal; that is, vy = 0. We are asked how long it will take the object to reach this point with θ = 30 degrees. Using the vertical-motion equation for vy , we can set it equal to 0 and solve for t:
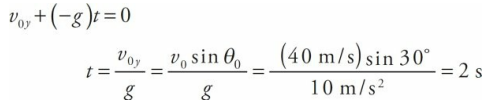
At this time, the projectile’s vertical displacement is
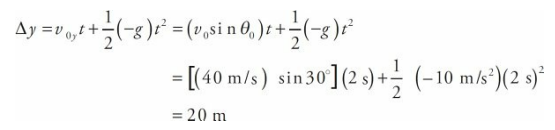
Free Fall
Free fall is a type of motion that occurs when an object falls under the influence of gravity alone, without any other forces acting upon it. In free fall, the object is said to be in a state of weightlessness, as it experiences zero apparent weight.
The acceleration experienced by an object in free fall is known as the acceleration due to gravity, denoted by the symbol 'g'. The value of 'g' is approximately 9.8 m/s^2 near the surface of the Earth, and is a constant value for all objects regardless of their mass.
The motion of an object in free fall can be described using the following equations of motion:
- Position: h = vi*t + (1/2)gt^2
- Velocity: v = vi + gt
- Acceleration: a = g
- where 'h' is the height of the object above the ground, 'vi' is the initial velocity of the object, 't' is the time elapsed, 'v' is the velocity of the object at time 't', and 'a' is the acceleration due to gravity.
In free fall, an object will continue to accelerate until it reaches its terminal velocity, which is the maximum velocity that the object can attain due to air resistance.
Once an object reaches its terminal velocity, it will continue to fall at a constant speed, as the upward force of air resistance balances the downward force of gravity.
Free Fall Sample Problem
A rock is dropped from an 80-meter cliff. How long does it take to reach the ground?
- Solution
- Since all of the rock’s motion is down, we call down the positive direction, so
a = +g. We’re given v0 , ∆y, and a, and we are asked for t. So v is missing; it isn’t given and it isn’t asked for, and we use Big Five #3:
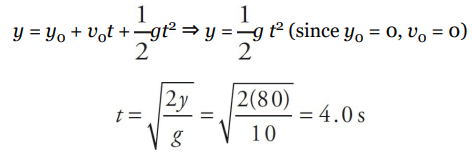
Kinematics with Graphs
Consider an object moving along a straight axis in such a way that its velocity, v, as a function of time, t, is given by the following velocity-vs.-time graph:
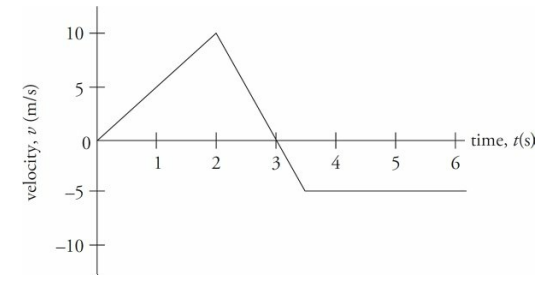
At time t = 0, the object’s velocity was v = 0. Over the first two seconds, its velocity increased steadily to 10 m/s. At time t = 2 s, the velocity then began to decrease (eventually becoming v = 0, at time t = 3 s). The velocity then became negative after t = 3 s, reaching v = –5 m/s at time t = 3.5 s. From t = 3.5 s on, the velocity remained a steady –5 m/s.
First, the fact that the velocity changed from t = 0 to t = 2 s tells us that the object accelerated. The acceleration during this time was
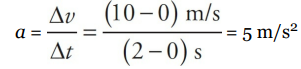
Note, however, that the ratio that defines the acceleration, ∆v/∆t, also defines the slope of the v-vs.-t graph. Therefore, “The slope of a velocity-vs.-time graph gives the average acceleration.“
What was the acceleration from time t = 2 s to time t = 3.5 s? The slope of the line segment joining the point (t, v) = (2 s, 10 m/s) to the point (t, v) = (3.5 s, –5 m/s) is
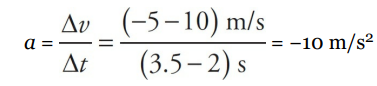
What is the object’s acceleration from time t = 3.5 s to time t = 6 s? Since the line segment from t = 3.5 s to t = 6 s is horizontal, its slope is zero, which indicates that the acceleration is zero, but you can also see this from looking at the graph; the object’s velocity did not change during this time interval.
Uniformly Accelerated Motion
- Uniformly accelerated motion is a type of motion where the acceleration of an object remains constant throughout its motion. This type of motion is characterized by the following equations:
v = u + at: This equation relates the final velocity (v) of an object to its initial velocity (u), acceleration (a), and time (t).s = ut + 1/2at^2: This equation relates the displacement (s) of an object to its initial velocity (u), acceleration (a), and time (t).v^2 = u^2 + 2as: This equation relates the final velocity (v) of an object to its initial velocity (u), acceleration (a), and displacement (s).
- Some key points to remember about uniformly accelerated motion are:
- The acceleration remains constant throughout the motion.
- The velocity of the object changes at a constant rate.
- The displacement of the object is directly proportional to the square of the time elapsed.
- Uniformly accelerated motion is commonly observed in free fall, where an object falls under the influence of gravity. In this case, the acceleration due to gravity is approximately constant and equal to 9.8 m/s^2.
The Big Five
- These five quantities are related by a group of five equations that we call the Big Five. They work in cases where acceleration is uniform, which are the ones we’re considering.
- Each of the Big Five equations is missing one of the five kinematic quantities.
- To decide which equation to use when solving a problem, determine which of the kinematic quantities is missing from the problem—that is, which quantity is neither given nor asked for—and then use the equation that doesn’t contain that variable.
| Equations | Missing Variable | |
|---|---|---|
| Big Five #1 | 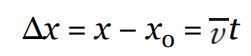 | a |
| Big Five #2 | 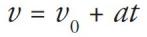 | ∆x |
| Big Five #3 | 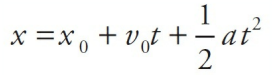 | v |
| Big Five #4 | 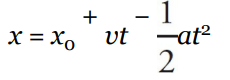 | v0 |
| Big Five #5 | 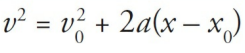 | t |
Unit 2: Newton's Laws of Motion
2.1: Newton's Laws of Motion: First and Second Law
Newton's First Law of Motion
- Also known as the law of inertia
- States that an object at rest will remain at rest, and an object in motion will remain in motion with a constant velocity, unless acted upon by an external force
- Inertia is the tendency of an object to resist changes in its motion
- The greater the mass of an object, the greater its inertia
- This law is important in understanding the behavior of objects in the absence of external forces, such as in space or in a vacuum
- It also explains why seat belts are important in cars, as they prevent passengers from continuing to move forward at the same speed when the car suddenly stops
- This law is the basis for the concept of momentum, which is the product of an object's mass and velocity
First Law Sample Problem
What net force is required to maintain a 5,000 kg object moving at a constant velocity of magnitude 7,500 m/s?
Solution
- The First Law says that any object will continue in its state of motion unless a force acts on it.
- Therefore, no net force is required to maintain a 5,000 kg object moving at a constant velocity of magnitude 7,500 m/s.
- Here’s another way to look at it: Constant velocity means a = 0, so the equation Fnet = ma immediately gives Fnet = 0.
Newton's Second Law of Motion
Newton's Second Law of Motion states that the acceleration of an object is directly proportional to the force applied to it and inversely proportional to its mass.
The formula for Newton's Second Law of Motion is F = ma, where F is the force applied, m is the mass of the object, and a is the acceleration produced.
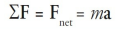
This law is also known as the law of acceleration.
The direction of the force applied determines the direction of the acceleration produced.
The greater the force applied, the greater the acceleration produced, and the greater the mass of the object, the smaller the acceleration produced.
This law is used to calculate the force required to move an object of a certain mass at a certain acceleration.
A force of 1 kg·m/s 2 is renamed 1 newton
Newton's Second Law of Motion is essential in understanding the behavior of objects in motion and is used in various fields such as engineering, physics, and sports.
Second Law Sample Problem
How much force is required to cause an object of mass 2 kg to have an acceleration of 4 m/s 2?
Solution
- According to the Second Law,
Fnet = ma = (2 kg)(4 m/s 2 ) = 8 N.
Friction Force
Friction force is a force that opposes motion between two surfaces that are in contact.
- It is caused by the irregularities in the surfaces that come into contact with each other.
- The force of friction acts parallel to the surfaces in contact and in the opposite direction to the direction of motion or the applied force.
There are three types of friction:
- Static Friction: It is the friction that exists between two surfaces that are not moving relative to each other. The static friction force is equal and opposite to the applied force until the applied force exceeds the maximum static friction force, after which the object starts moving.
- Kinetic Friction: It is the friction that exists between two surfaces that are moving relative to each other. The kinetic friction force is constant and is less than the maximum static friction force.
- Rolling Friction: It is the friction that exists between a rolling object and the surface it is rolling on. Rolling friction is less than static and kinetic friction.
The factors that affect friction are:
- Nature of the Surfaces: The nature of the surfaces in contact affects the friction force. Rough surfaces have more friction than smooth surfaces.
- Normal Force: The normal force is the force exerted by a surface perpendicular to the surface in contact. The friction force is directly proportional to the normal force.
- Surface Area: The surface area in contact affects the friction force. The larger the surface area in contact, the greater the friction force.
The strengths of these two types of friction forces are given by the following equations:
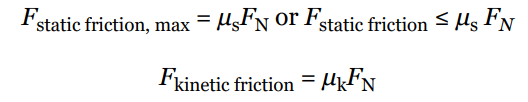
Weight
The weight of an object is the gravitational force exerted on it by a gravitational field.
Mass is an intrinsic property of an object that measures its inertia. An object’s mass does not change with location.
Since weight is a force, we can use F = ma to compute it, where the acceleration is the gravitational force imposed on an object. Therefore, setting a = g, the equation F = ma becomes
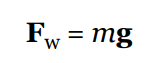
The Normal Force
- The component of the contact force that’s perpendicular to the surface is called the normal force on the object.
- The normal force comes from electrostatic interactions among atoms.
- The normal force is what prevents objects from falling through tabletops or you from falling through the floor.
- The normal force is denoted by FN, or simply by N.
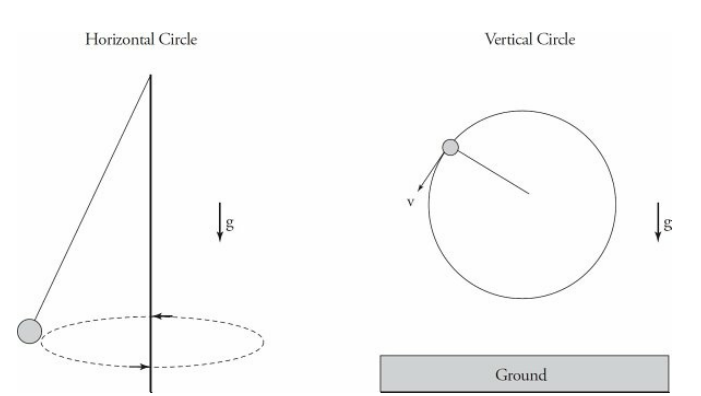
2.2: Uniform Circular Motion
- Uniform circular motion is the motion of an object moving in a circular path at a constant speed. The direction of the velocity of the object is constantly changing, but the magnitude of the velocity remains constant.
- In order for an object to move in a circular path, there must be a force acting on it towards the center of the circle. This force is called the centripetal force. The magnitude of the centripetal force is given by the equation:
F = (mv^2)/r- where F is the centripetal force, m is the mass of the object, v is the speed of the object, and r is the radius of the circle.
- Centrifugal force is a fictitious force that appears to act on an object moving in a circular path. It is not a real force, but rather an apparent force that arises from the fact that the object is moving in a curved path. The centrifugal force is equal in magnitude and opposite in direction to the centripetal force.
The following diagrams show examples of a ball on a string traveling in a horizontal circle and a vertical circle.
UCM Sample Problem
Example 1
An object of mass 5 kg moves at a constant speed of 6 m/s in a circular path of radius 2 m. Find the object’s acceleration and the net force responsible for its motion.
Solution
By definition, an object moving at constant speed in a circular path is undergoing uniform circular motion. Therefore, it experiences a centripetal acceleration of magnitude v 2/r, always directed toward the center of the circle:
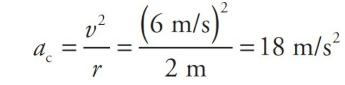
The force that produces the centripetal acceleration is given by Newton’s Second Law, coupled with the equation for centripetal acceleration:
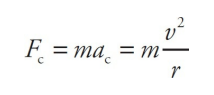
Example 2
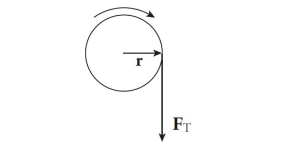
A 10 kg mass is attached to a string that has a breaking strength of 200 N. If the mass is whirled in a horizontal circle of radius 80 cm, what maximum speed can it have? Assume the string is horizontal.
Solution
The first thing to do in problems like this is to identify what force(s) provide the centripetal force. In this example, the tension in the string (FT ) provides the centripetal force (Fc):
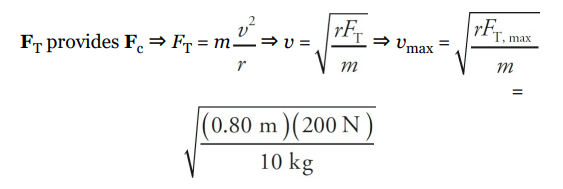
2.3: Newton's Third Law of Motion
- Newton's Third Law of Motion states that for every action, there is an equal and opposite reaction.
- This means that when an object exerts a force on another object, the second object exerts an equal and opposite force back on the first object.
- The forces are always of the same type, either both are attractive or both are repulsive.
- The Third Law applies to all types of forces, including gravitational, electromagnetic, and nuclear forces.
- The Third Law is important in understanding how objects move and interact with each other.
- It explains why rockets are able to launch into space and why cars are able to move forward.
- The Third Law also helps explain why collisions occur and how they affect the objects involved.
- It is important to note that the forces in the Third Law always act on different objects, not on the same object.
Pulleys
Pulleys are devices that change the direction of the tension force in the cords that slide over them.
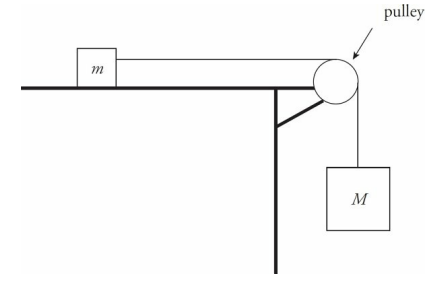
Pulley Sample Problem
In the diagram above, assume that the tabletop is frictionless. Determine the acceleration of the blocks once they’re released from rest.
Solution
There are two blocks, so draw two free-body diagrams: The positive directions for each block must coincide. If the block on the table travels to the right then the hanging block travels down. This is why down is positive for the hanging block.
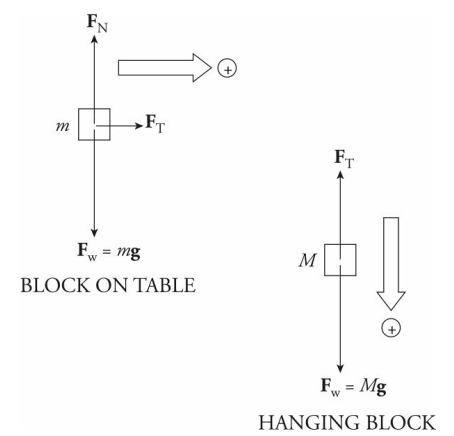
To get the acceleration of each one, we use Newton’s Second Law, Fnet = ma. Notice that while Fw = FN for the block on the table, Fw does not equal FT for the hanging block, because that block is in motion in the downward direction.
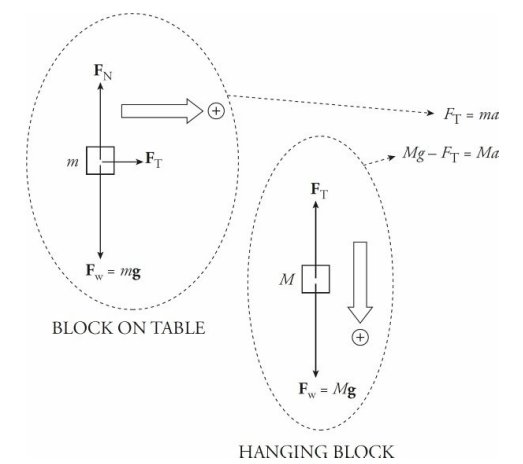
Note that there are two unknowns, FT and a, but we can eliminate FT by adding the two equations, and then we can solve for a.

Inclined Planes
An inclined plane is basically a ramp. If an object of mass m is on the ramp, then the force of gravity on the object, Fw = mg, has two components: One that’s parallel to the ramp (mg sin θ) and one that’s normal to the ramp (mg cos θ), where θ is the incline angle.
The force driving the block down the inclined plane is the component of the block’s weight that’s parallel to the ramp: mg sin θ.
When analyzing objects moving up or down inclined planes it is almost always easiest to rotate the coordinate axes such that the x-axis is parallel to the incline and the y-axis is perpendicular to the incline, as shown in the diagram.
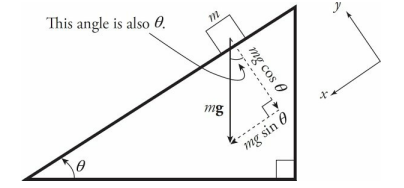
The object would accelerate in both the xand y-directions as it moved down along the incline if you did not rotate the axis. However, with the rotated axes, the acceleration in the y-direction is zero. Now we only have to worry about the acceleration in the x-direction.
Inclined Planes Sample Problem
A block slides down a frictionless inclined plane that makes a 30° angle with the horizontal. Find the acceleration of this block.
Solution
Let m denote the mass of the block, so the force that pulls the block down the incline is mg sin θ, and the block’s acceleration down the plane is
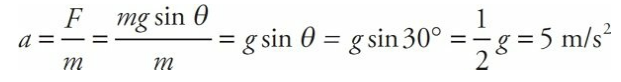
Unit 3: Work Energy and Power
3.1: Work-Energy Theorem
Work
If F is the force, and dr is an infinitesimal amount of displacement, then the work done is:
W = ∫F · dr- If the force is constant, it can be removed from of the integral, and since
F · r = (F cosθ)r for any angle θ, thenW = (F cos θ)r. The unit of work is the newton-meter (N·m), which is also called a joule (J).
- If the force is constant, it can be removed from of the integral, and since
Work Sample Problem #1
You slowly lift a book of mass 2 kg at constant velocity through a distance of 3 m. How much work did you do on the book?
- Solution Problem #1
- In this case, the force you exert must balance the weight of the book (other-wise the velocity of the book wouldn’t be constant), so
F = mg = (2 kg)(10 m/s 2 ) = 20 N.- Since this force is straight upward and the displacement, d, of the book is also straight upward, F and d are parallel, so the work done by your lifting force is
W = Fd = (20 N) (3 m) = 60 N·m = 60 J.- Work Sample Problem #2
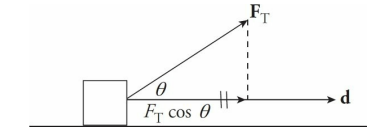
A 15 kg crate is moved along a horizontal floor by a warehouse worker who’s pulling on it with a rope that makes a 30° angle with the horizontal. The tension in the rope is 200 N and the crate slides a distance of 10 m. How much work is done on the crate by the rope?
- Solution Problem #2
- The figure below shows that FT and d are not parallel. It’s only the component of the force acting along the direction of motion, FT cos θ, that does work.
Therefore,
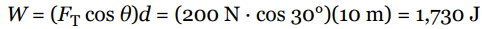
Kinetic Energy
- Kinetic energy is the energy possessed by an object due to its motion. It is a scalar quantity and is dependent on the mass and velocity of the object. The formula for kinetic energy is:
KE = 1/2 * m * v^2- where KE is the kinetic energy, m is the mass of the object, and v is the velocity of the object.
- The SI unit of kinetic energy is joules (J). However, it can also be expressed in other units such as calories, electronvolts, and foot-pounds.
- In a closed system, the total kinetic energy remains constant. This is known as the conservation of kinetic energy. It means that the kinetic energy can be transferred from one object to another, but the total amount of kinetic energy in the system remains the same.
Work Energy Theorem
The derivation above can be extended to an object with a non-zero initial speed, and the same analysis will show that the total work done on an object—or, equivalently, the work done by the net force—will equal its change in kinetic energy; this is known as the work–energy theorem:
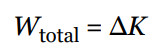
Work Energy Theorem Sample Problem #1
What is the kinetic energy of a ball (mass = 0.10 kg) moving with a speed of 30 m/s?
- Solution Problem #1
- \
- Work Energy Theorem Sample Problem #2
A tennis ball (mass = 0.06 kg) is hit straight upward with an initial speed of 50 m/s. How high would it go if air resistance were negligible?
- Solution Problem #2
- This could be done using the Big Five, but let’s try to solve it using the concepts of work and energy. As the ball travels upward, gravity acts on it by doing negative work. [The work is negative because gravity is opposing the upward motion.
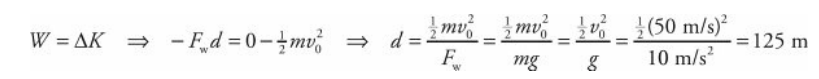
Potential Energy
- Potential energy is the energy possessed by an object due to its position or state. It is the energy that an object has stored within itself, which can be released when the object is allowed to move or change its state.
- Types of Potential Energy
- Gravitational Potential Energy: It is the energy possessed by an object due to its position in a gravitational field. The higher an object is placed, the greater its gravitational potential energy.
- Elastic Potential Energy: It is the energy possessed by an object due to its deformation or stretching. The more an object is stretched, the greater its elastic potential energy.
- Chemical Potential Energy: It is the energy possessed by an object due to the arrangement of its atoms or molecules. The more energy stored in the chemical bonds, the greater the chemical potential energy.
- The formula for potential energy is given by:
PE = mgh- where PE is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object.
- Potential Energy Sample Problem #1
A stuntwoman (mass = 60 kg) scales a 40-meter-tall rock face. What is her gravitational potential energy (relative to the ground)?
- Solution Problem #1
- Calling the ground h = 0, we find
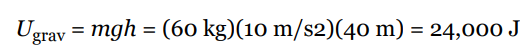
- Potential Energy Sample Problem #2
If the stuntwoman in the previous example were to jump off the cliff, what would be her final speed as she landed on a large, air-filled cushion lying on the ground?
- Solution Problem #2
- The gravitational potential energy would be transformed into kinetic energy. So
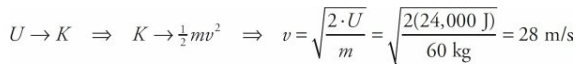
3.2: Conservation of Energy
The sum of an object’s kinetic and potential energies is called its mechanical energy, E:
E = K + U.Assuming that no nonconservative forces (friction, for example) act on an object or system while it undergoes some change, then mechanical energy is conserved. That is, the initial mechanical energy, Ei , is equal to the final mechanical energy, Ef , or
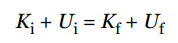
- This is the simplest form of the Law of Conservation of Total Energy, which we mentioned at the beginning of this section.
Conservation of Energy Sample Problem
A ball of mass 2 kg is dropped from a height of 5.0 m above the floor. Find the speed of the ball as it strikes the floor.
Solution
Ignoring the friction due to the air, we can apply Conservation of Mechanical Energy. Calling the floor our h = 0 reference level, we write
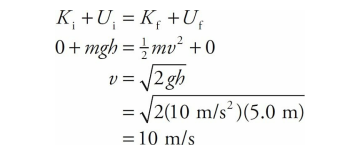
Note that the ball’s potential energy decreased, while its kinetic energy increased. This is the basic idea behind conservation of mechanical energy: One form of energy decreases while the other increases.
Potential Energy Curves
- Potential energy curves are graphical representations of the potential energy of a system as a function of the distance between two or more particles.
- These curves are used to study the behavior of molecules, atoms, and other particles in a system.
- The shape of the potential energy curve depends on the type of interaction between the particles in the system.
- The potential energy curve for a simple harmonic oscillator is a parabola, while the curve for a diatomic molecule is more complex.
- The potential energy curve for a diatomic molecule has two minima, corresponding to the equilibrium bond length and the dissociation limit.
- The potential energy curve for a polyatomic molecule has many minima and maxima, corresponding to the different conformations of the molecule.
Conservation of Energy Sample Problem
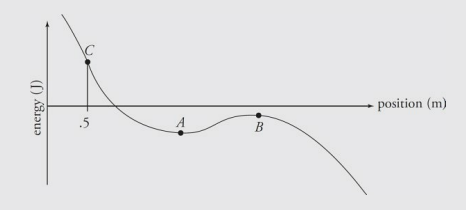
An object of mass m = 4 kg has a potential energy function U(x) = (x – 2) – (2x – 3)^3; Where x is measured in meters and U in joules. The following graph is a sketch of the potential energy function.
(a) Determine the positions of points A and B, the equilibrium points. (b) If the object is released from rest at the point B, can it reach point A or C? Explain. (c) The particle is released from rest at point C. Determine its speed as it passes point A.
\
\
Solution
The points A and B are a local minimum and maximum, respectively, so the derivative of U(x) will be zero at these locations.
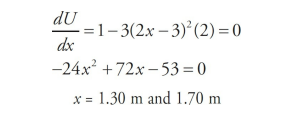
The object has a negative total amount of mechanical energy at point B because all of its energy is potential energy. It will not be able to reach point C, because that position has a potential energy well above zero.
- However the object would be able to reach point A because the potential energy at A is less than the energy the object started with at point B. As the object moved from B to A its potential energy would decrease (become more negative) and its kinetic energy would increase.
First, we need to find how much potential energy the object has at point C, and this will define the total mechanical energy of the object. Then determine the potential energy at point A, x = 1.3 m, and use conservation of energy to determine the speed at point A.
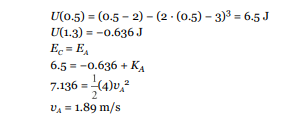
3.3: Power
Power is the rate at which work gets done (or energy gets transferred, which is the same thing). Suppose you and I each do 1,000 J of work, but I do the work in 2 minutes while you do it in 1 minute. We both did the same amount of work, but you did it more quickly; you were more powerful.
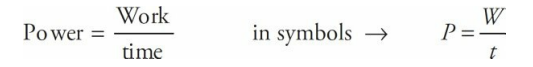
Since power is a rate, it can be represented as a derivative, too. The calculus (rather than algebra) equation for power is:
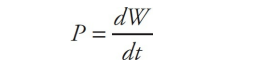
Power Sample Problem #1
A mover pushes a large crate (mass m = 75 kg) from the inside of the truck to the back end (a distance of 6 m), exerting a steady push of 300 N. If he moves the crate this distance in 20 s, what is his power output during this time?
- Solution Problem #1
- The work done on the crate by the mover is
W = Fd = (300N)(6 m) = 1,800 J.- If this much work is done in 20 s, then the power delivered is
P = W/t = (1,800 J)/(20 s) = 90 W.- Power Sample Problem #2
What must be the power output of a rocket engine, which moves a 1,000 kg rocket at a constant speed of 8.0 m/s?
- Solution Problem #2
- The equation P = Fv, with F = mg, yields
P = mgv = (1,000 kg)(10 N/kg)(8.0 m/s) = 80,000 W = 80 kW
Unit 4: Systems of Particles and Linear Momentum
4.1: Center of Mass
The center of mass is the point where all of the mass of an object can be considered to be concentrated; it’s the dot that represents the object of interest in a free-body diagram.
For a homogeneous body (that is, one for which the density is uniform throughout), the center of mass is where you intuitively expect it to be: at the geometric center. Thus, the center of mass of a uniform sphere or cube or box is at its geometric center.
If we have a collection of discrete particles, the center of mass of the system can be determined mathematically as follows.
First consider the case where the particles all lie on a straight line. Call this the x-axis.
Select some point to be the origin (x = 0) and determine the positions of each particle on the axis.
Multiply each position value by the mass of the particle at that location, and get the sum for all the particles. Divide this sum by the total mass, and the resulting x-value is the center of mass:
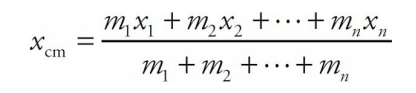
The system of particles behaves in many respects as if all its mass,
M = m1 + m2 +···+ mn, were concentrated at a single location, xcm.If the system consists of objects that are not confined to the same straight line, use the equation above to find the x-coordinate of their center of mass, and the corresponding equation,
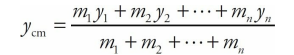
- to find the y-coordinate of their center of mass (and one more equation to calculate the z-coordinate, if they are not confined to a single plane).
From the equation
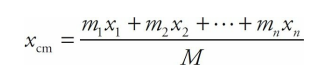
we can derive
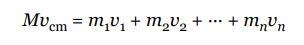
So, the total linear momentum of all the particles in the system
(m1v1 + m2v2 +…+ mnvn )is the same as Mvcm, the linear momentum of a single particle (whose mass is equal to the system’s total mass) moving with the velocity of the center of mass.We can also differentiate again and establish the following:
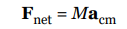
This says that the net (external) force acting on the system causes the center of mass to accelerate according to Newton’s Second Law.
Sample Problem
A bar with a length of 30 cm has a linear density λ = 10 + 6x, where x is in meters and λ is in kg/m. Determine the mass of the bar and the center of mass of this bar.
Solution
We can determine the mass of the bar by using the definition of linear density, therefore..
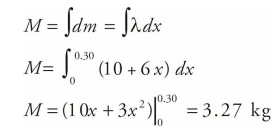
To calculate the center of mass, we will use this equation:
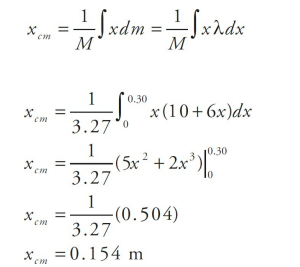
Motion of the Center of Mass
- The center of mass (COM) is the point in a system where the mass can be considered to be concentrated.
- If there is no external force acting on a system, the COM will remain at rest or move with a constant velocity.
- If there is an external force acting on a system, the COM will accelerate in the direction of the force.
- The acceleration of the COM is related to the net force acting on the system and the total mass of the system through the equation F = ma, where F is the net force, m is the total mass, and a is the acceleration of the COM.
- The motion of the COM can be used to analyze the motion of a system as a whole, rather than analyzing the motion of each individual particle in the system.
- The motion of the COM can also be used to determine the stability of a system. A system is stable if the COM is at a low point in its potential energy, and unstable if the COM is at a high point in its potential energy.
Center of Gravity vs Center of Mass
- Center of Gravity
- The center of gravity is the point where the weight of an object is evenly distributed in all directions.
- It is the point where the object can be balanced perfectly.
- It is the point where the gravitational force on the object is concentrated.
- It is dependent on the distribution of mass and the gravitational field.
- Center of Mass
- The center of mass is the point where the mass of an object is evenly distributed in all directions.
- It is the point where the object can be balanced perfectly.
- It is the point where the gravitational force on the object is concentrated.
- It is dependent on the distribution of mass only.
- Difference between Center of Gravity and Center of Mass
- The center of gravity is dependent on both the distribution of mass and the gravitational field, while the center of mass is dependent only on the distribution of mass.
- The center of gravity is used in statics, while the center of mass is used in dynamics.
- The center of gravity can change with the position of the object, while the center of mass remains constant.
- The center of gravity is used in engineering and design, while the center of mass is used in physics and mechanics.
4.2: Impulse and Momentum
The product of force and the time during which it acts is known as impulse; it’s a vector quantity that’s denoted by J:
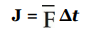
In terms of impulse, Newton’s Second Law can be written in yet another form:
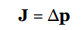
Sometimes this is referred to as the impulse–momentum theorem, but it’s just another way of writing Newton’s Second Law. If F varies with time over the interval during which it acts, then the impulse delivered by the force F = F(t) from time t = t1 to t = t2 is given by the following definite integral:
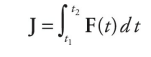
On the equation sheet for the free-response section, this information will be represented as follows:
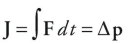
If a graph of force-versus-time is given, then the impulse of force F as it acts from t1 to t2 is equal to the area bounded by the graph of F, the t-axis, and the vertical lines associated with t1 and t2 as shown in the following graph.
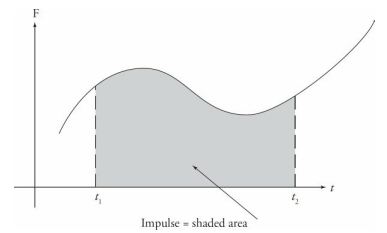
Sample Problem
A football team’s kicker punts the ball (mass = 0.4 kg) and gives it a launch speed of 30 m/s. Find the impulse delivered to the football by the kicker’s foot and the average force exerted by the kicker on the ball, given that the impact time is 8 ms.
Solution
Impulse is equal to change in linear momentum, so
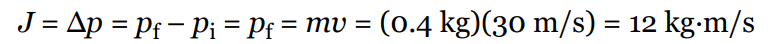
Using the equation F = J/Δt, we find that the average force exerted by the kicker is
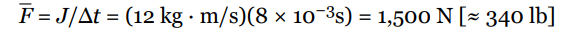
4.3: Conservation of Linear Momentum
Linear momentum is the product of an object's mass and velocity.
The conservation of linear momentum states that the total momentum of a closed system of objects remains constant if no external forces act on the system. This means that the sum of the momenta of all the objects in the system before a collision or interaction is equal to the sum of the momenta after the collision or interaction.
In equation form, for two objects colliding, we have
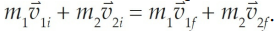
Conservation of Linear Momentum Sample Problem
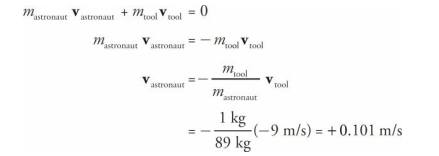
An astronaut is floating in space near her shuttle when she realizes that the cord that’s supposed to attach her to the ship has become disconnected. Her total mass (body + suit + equipment) is 89 kg. She reaches into her pocket, finds a 1 kg metal tool, and throws it out into space with a velocity of 9 m/s directly away from the ship. If the ship is 10 m away, how long will it take her to reach it?
Solution
Here, the astronaut + tool are the system. Because of Conservation of Linear Momentum,
Using distance = average speed × time, we find
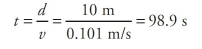
Collisions
- The objects whose collision we will analyze form the system, and although the objects exert forces on each other during the impact, these forces are only internal (they occur within the system). The system’s total linear momentum is conserved if there is no net external force on the system.
- Collisions are classified into two major categories: (1) elastic and (2) inelastic. A collision is said to be elastic if kinetic energy is conserved. Inelastic collisions, then, are ones in which the total kinetic energy is different after the collision.
- An extreme example of inelasticism is completely (or perfectly or totally) inelastic.
Collisions Sample Problem
Two balls roll toward each other, one red and the other green. The red ball has a mass of 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2 m/s. After the head-on collision, the red ball continues forward with a speed of 1.7 m/s. Find the speed of the green ball after the collision. Was the collision elastic?
Solution
First remember that momentum is a vector quantity, so the direction of the velocity is crucial. Since the balls roll toward each other, one ball has a positive velocity while the other has a negative velocity. Let’s call the red ball’s velocity before the collision positive; then vred = +4 m/s, and vgreen = –2 m/s. Using a prime to denote after the collision, Conservation of Linear Momentum gives us the following:
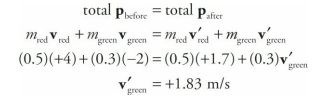
Notice that the green ball’s velocity was reversed as a result of the collision; this typically happens when a lighter object collides with a heavier object. To see whether the collision was elastic, we need to compare the total kinetic energies before and after the collision.
In this case, however, an explicit calculation is not needed since both objects experienced a decrease in speed as a result of the collision. Kinetic energy was lost, so the collision was inelastic; this is usually the case with macroscopic collisions.
Most of the lost energy was transferred as heat; the two objects are both slightly warmer as a result of the collision
Unit 5: Rotation
5.1: Torque and Rotational Inertia
Torque is a measure of the twisting force that causes rotation.
It is defined as the product of force and the perpendicular distance from the axis of rotation to the line of action of the force.
Torque can be calculated using the formula below where T is torque, F is force, r is the moment arm, and theta is the angle between the force and the moment arm.
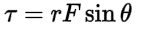
The unit of torque is Newton-meter (Nm) or pound-feet (lb-ft).
Torque is a vector quantity, which means it has both magnitude and direction.
The direction of torque is perpendicular to the plane of rotation and follows the right-hand rule.
Torque is important in many applications, such as engines, motors, and machines.
In engines, torque is used to measure the power output of the engine and is often expressed in horsepower (hp).
Torque can be increased by increasing the force applied or by increasing the distance from the axis of rotation.
The moment arm is the perpendicular distance from the axis of rotation to the line of action of the force and is an important factor in determining torque.
Torque is also related to angular acceleration and moment of inertia, which are important concepts in rotational motion.
Sample Problem (Torque)
A student pulls down with a force of 40 N on a rope that winds around a pulley of radius 5 cm. What’s the torque of this force?
Therefore, the torque produced by this tension force is simply
\
Rotational Inertia
- Rotational inertia, also known as moment of inertia, is the property of an object that determines its resistance to rotational motion. It depends on the mass distribution of the object and the axis of rotation.
- The formula for rotational inertia is:
I = ∫ r^2 dm- where I is the rotational inertia, r is the distance from the axis of rotation to the element of mass dm, and the integral is taken over the entire mass of the object.
- The units of rotational inertia are kg m^2.
Sample Problem (Rotational Inertia)
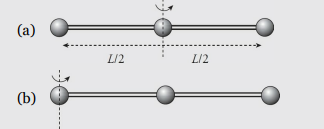
Three beads, each of mass m, are arranged along a rod of negligible mass and length L. Figure out the rotational inertia of the assembly when the axis of rotation is through the center bead and when the axis of rotation is through one of the beads on the ends.
\
\
Solution
In the first case, both the left bead and the right bead are at a distance of L/2 from the axis of rotation, while the center bead is at distance zero from the axis of rotation. Therefore,
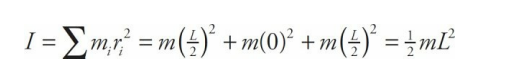
In the second case, the left bead is at distance zero from the rotation axis, the center bead is at distance L/2, and the right bead is at distance L. Therefore,
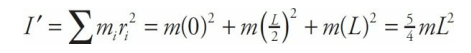
Parallel Axis Theorem
The parallel axis theorem is a principle in physics that relates to the moment of inertia of a rigid body.
- It states that the moment of inertia of a body about any axis parallel to its center of mass is equal to the moment of inertia about the center of mass plus the product of the mass of the body and the square of the distance between the two axes.
The formula for the parallel axis theorem is:
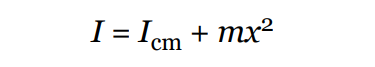
- where I is the moment of inertia about the parallel axis, I_cm is the moment of inertia about the center of mass, m is the mass of the body, and d is the distance between the two axes.
The parallel axis theorem is used in various fields of physics and engineering. Some of its applications are:
- It is used to calculate the moment of inertia of complex objects that cannot be easily calculated using other methods.
- It is used in the design of machines and structures to determine their stability and resistance to rotation.
- It is used in the study of celestial mechanics to calculate the moment of inertia of planets and other celestial bodies.
- It is used in the study of molecular biology to calculate the moment of inertia of molecules and their rotational motion.
The parallel axis theorem is based on certain assumptions and has some limitations. Some of them are:
- It assumes that the body is rigid and does not deform under the applied forces.
- It assumes that the mass of the body is distributed uniformly.
- It assumes that the distance between the two axes is small compared to the size of the body.
- It does not take into account the effects of external forces such as friction and air resistance.
5.2: Rotational Kinematics
Mark several dots along a radius on a disk, and call this radius the reference line. If the disk rotates about its center, we can use the movement of these dots to talk about angular displacement, angular velocity, and angular acceleration.
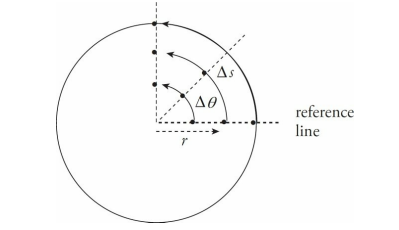
If the disk rotates as a rigid body, then all three dots shown have the same angular displacement, ∆θ. In fact, this is the definition of a rigid body: All points along a radial line always have the same angular displacement.
Just as the time rate-of-change of displacement gives velocity, the time rate-of-change of angular displacement gives angular velocity, denoted by ω (omega). The definition of the average angular velocity is:
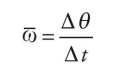
Note that if we let the time interval ∆t approach 0, then the equation above leads to the definition of the instantaneous angular velocity:
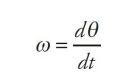
And, finally, just as the time rate-of-change of velocity gives acceleration, the time rate-of-change of angular velocity gives angular acceleration, or α (alpha). The definition of the average angular acceleration is:
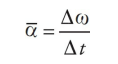
If we let the time interval ∆t approach 0, then the equation above leads to the definition of the instantaneous angular acceleration:
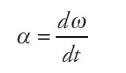
On the rotating disk illustrated on the previous page, we said that all points undergo the same angular displacement in any given time interval; this means that all points on the disk have the same angular velocity, ω, but not all points have the same linear velocity, v. This follows from the definition of radian measure. Expressed in radians, the angular displacement, ∆θ, is related to the arc length, ∆s, by the equation
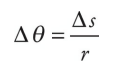
Rearranging this equation and dividing by ∆t, we find that
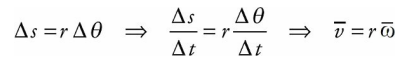
Or, using the equations v = ds/dt and ω = dθ/dt,
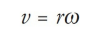
Therefore, the greater the value of r, the greater the value of v. Points on the rotating body farther from the rotation axis move more quickly than those closer to the rotation axis.
From the equation v = rω, we can derive the relationship that connects angular acceleration and linear acceleration. Differentiating both sides with respect to t (holding r constant), gives us
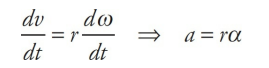
Sample Problem
The angular velocity of a rotating disk increases from 2 rad/s to 5 rad/s in 0.5 s. What’s the disk’s average angular acceleration?
Solution
The Big Five for Rotational Motion
- These five quantities are interrelated by a group of five equations which we call the Big Five. They work in cases in which the angular acceleration is uniform. These equations are identical to the Big Five in Kinematics but, in these cases, the translational variables (s, v, or a) are replaced by the corresponding rotational variables (θ, ω, or α, respectively).
| Equation | Missing Variables | |
|---|---|---|
| Big Five #1 | 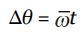 | α |
| Big Five #2 | 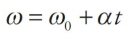 | ∆θ |
| Big Five #3 | 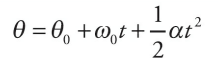 | ω |
| Big Five #4 | 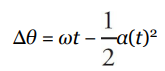 | ω0t |
| Big Five #5 | 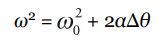 |
5.3: Rotational Dynamics and Energy
Definition of Rotational Kinetic Energy
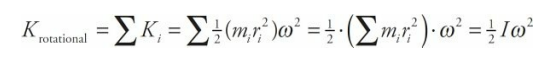
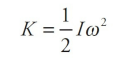
Rolling Motion
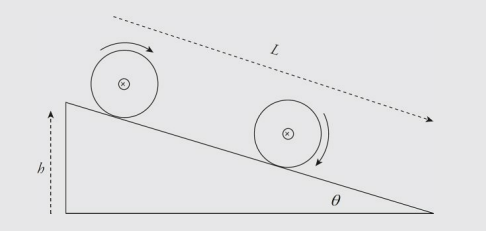
One of the main types of motion associated with rotational motion is rolling motion. We will primarily deal with rolling motion without slipping. Consider a disk rolling down an incline—without slipping:
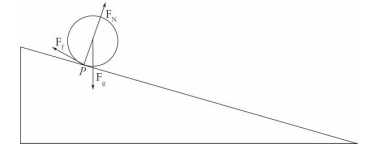
The point of contact of the object with the surface P is instantaneously at rest. If this were not the case, then the disk would be slipping down the incline, so the contact point must not be moving relative to the surface. In this case, the velocity of the center of mass of the disk is equal to the radius times the angular velocity of the disk.
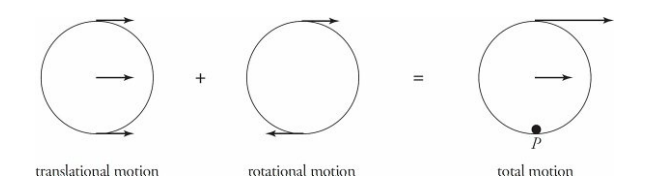
The total motion for an object that is rolling without slipping is the combined motion of the entire object translating with the velocity of the center of mass, and the object rotating about its center of mass, as shown below. This shows the object is instantaneously rotating about the contact point P.
For rolling motion the total kinetic energy is the translational kinetic energy and the rotational kinetic energy.
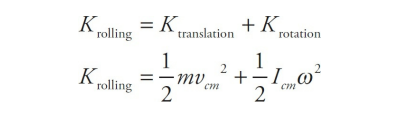
Sample Problem (Rolling Motion)
A cylinder of mass M and radius R rolls (without slipping) down an inclined plane (of height h and length L) whose incline angle with the horizontal is θ. Determine the linear speed of the cylinder’s center of mass when it reaches the bottom of the incline (assuming that it started from rest at the top).
\
\
Solution
As the cylinder rolls down the ramp, its initial gravitational potential energy is converted into kinetic energy, which is a combination of translational kinetic energy (since the cylinder’s center of mass is translating down the ramp) and rotational kinetic energy:
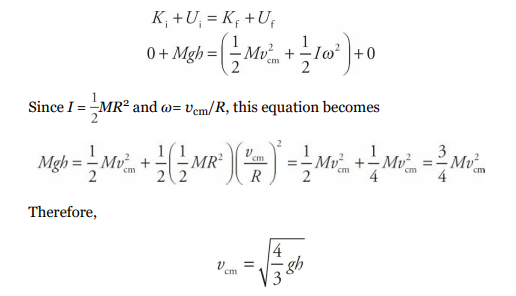
We can verify this result using the result of the previous example. There we found that the acceleration of the cylinder’s center of mass as it rolled down the ramp was a = 2/3gsin θ. Applying Big Five #5 gives us:
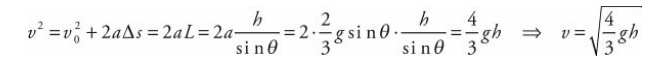
5.4: Angular Momentum
Newton’s Second Law says that
Fnet = dp/dtso if Fnet = 0, then p is constant. This is Conservation of Linear Momentum. The rotational analog of this is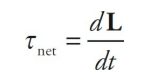
So if τnet = 0, then L is constant. This is Conservation of Angular Momentum. Basically, this says that if the torques on a body balance so that the net torque is zero, then the body’s angular momentum can’t change.
Sample Problem (Angular Momentum)
A child of mass m = 30 kg stands at the edge of a small merry-go-round that’s rotating at a rate of 1 rad/s. The merry-go-round is a disk of radius R = 2.5 m and mass M = 100 kg. If the child walks in toward the center of the disk and stops 0.5 m from the center, what will happen to the angular velocity of the merry-go-round (if friction can be ignored)?
Solution
The child walking toward the center of the merry-go-round does not provide an external torque to the child + disk system, so angular momentum is conserved. Let’s denote the child as a point mass, and consider the following two views of the merry-go-round (looking down from above):
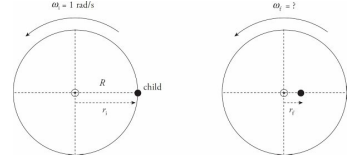
In the first picture, the total rotational inertia, Ii , is equal to the sum of the rotational inertia of the merry-go-round (MGR) and the child:

In the second picture, the total rotational inertia has decreased to
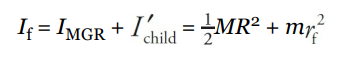
So, by Conservation of Angular Momentum, we have
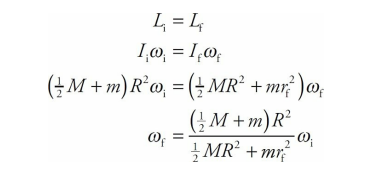
and substituting the given numerical values gives us
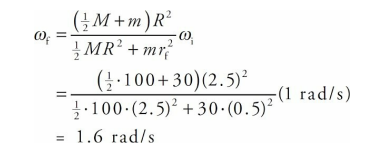
Notice that ω increased as I decreased, just as Conservation of Angular Momentum predicts.
Equilibrium
- Equilibrium in rotational motion occurs when an object is not rotating or is rotating at a constant angular velocity. This means that the net torque acting on the object is zero.
- For an object to be in equilibrium in rotational motion, the following conditions must be met:
- The net torque acting on the object must be zero.
- The object must be at rest or rotating at a constant angular velocity.
- There are two types of equilibrium in rotational motion:
- Static equilibrium: This occurs when an object is at rest and the net torque acting on it is zero.
- Dynamic equilibrium: This occurs when an object is rotating at a constant angular velocity and the net torque acting on it is zero.
Unit 6: Oscillations
6.1: Simple Harmonic Motion
When a spring is compressed or stretched from its natural length, a force is created. If the spring is displaced by x from its natural length, the force it exerts in response is given by the equation
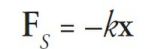
This is known as Hooke’s law. The proportionality constant, k, is a positive number called the spring (or force) constant that indicates how stiff the spring is. The stiffer the spring, the greater the value of k. The minus sign in Hooke’s law tells us that FS and x always point in opposite directions.
Sample Problem (SHM)
A 12 cm-long spring has a force constant (k) of 400 N/m. How much force is required to stretch the spring to a length of 14 cm?
Solution
- The displacement of the spring has a magnitude of 14 – 12 = 2 cm = 0.02 m so, according to Hooke’s law, the spring exerts a force of magnitude F = –kx = –(400 N/m)(0.02 m) = –8 N. This is the restoring force, so we’d have to exert a force of 8 N to keep the spring in this stretched state.
6.2: Simple Harmonic Motion in Terms of Energy
A stretched or compressed spring stores elastic potential energy, which is transformed into kinetic energy (and back again). This shuttling between potential and kinetic energy causes the oscillations. For a spring with spring constant k, the elastic potential energy it possesses—relative to its equilibrium position—is given by the equation
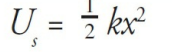
In terms of energy transfers, we can describe the block’s oscillations as follows: When you initially pull the block out, you increase the elastic potential energy of the system. Upon releasing the block, this potential energy turns into kinetic energy, and the block moves.
- As it passes through its equilibrium position, Us = 0. Then, as the block continues through that position, the spring is compressed, and the kinetic energy is transformed back into elastic potential energy.
By Conservation of Mechanical Energy, the sum K + Us is a constant. Therefore, when the block reaches the maximum displacement, Us is maximized, so K must be minimized; in fact, K = 0 at the endpoints of the oscillation region. As the block is passing through equilibrium, x = 0, so Us = 0 and K is maximized.
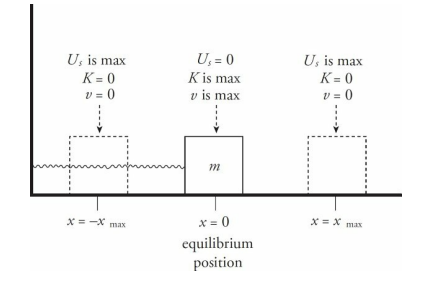
The maximum displacement from equilibrium is called the amplitude of oscillation and is denoted by A. So instead of writing x = xmax , we write x = A.
Sample Problem
A block of mass m = 0.05 kg oscillates on a spring whose force constant k is 500 N/m. The amplitude of the oscillations is 4.0 cm. Calculate the maximum speed of the block.
Solution
First, let’s get an expression for the maximum elastic potential energy of the system:
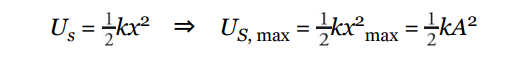
When all this energy has been transformed into kinetic energy—which occurs at the equilibrium position—the block will have maximum kinetic energy and maximum speed
6.3: Kinematics of Simple Harmonic Motion
As you watch the block oscillate, you should notice that it repeats each cycle of oscillation in the same amount of time.
- A cycle is a roundtrip: for example, from position x = A over to x = –A and back again to x = A.
- The amount of time it takes to complete a cycle is called the period of the oscillations, or T.
- If T is short, the block is oscillating rapidly, and if T is long, the block is oscillating slowly.
Another way of indicating the rapidity of the oscillations is to count the number of cycles that can be completed in a given time interval: the greater the number of completed cycles, the more rapid the oscillations.
- The number of cycles that can be completed per unit time is called the frequency of the oscillations, or f, and is expressed in cycles per second.
- One cycle per second is one hertz.
One of the most basic equations of oscillatory motion expresses the inverse relationship between period and frequency:
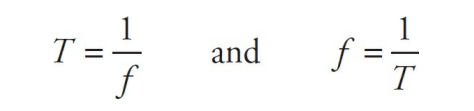
Sample Problem
A block oscillating on the end of a spring moves from its position of maximum spring stretch to maximum spring compression in 0.25 s. Determine the period and frequency of this motion.
Solution
- The period is defined as the time required for one full cycle.
- Moving from one end of the oscillation region to the other is only half a cycle.
- Therefore, if the block moves from its position of maximum spring stretch to maximum spring compression in 0.25 s, the time required for a full cycle is twice as much; T = 0.5 s.
- Because frequency is the reciprocal of period, the frequency of the oscillations is f = 1/T = 1/(0.5 s) = 2 Hz.
6.4: The Spring-Block Oscillator: Vertical Motion
Consider a spring of negligible mass hanging from a stationary support. A block of mass m is attached to its end and allowed to come to rest, stretching the spring a distance d. At this point, the block is in equilibrium; the upward force of the spring is balanced by the downward force of gravity. Therefore,
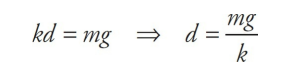
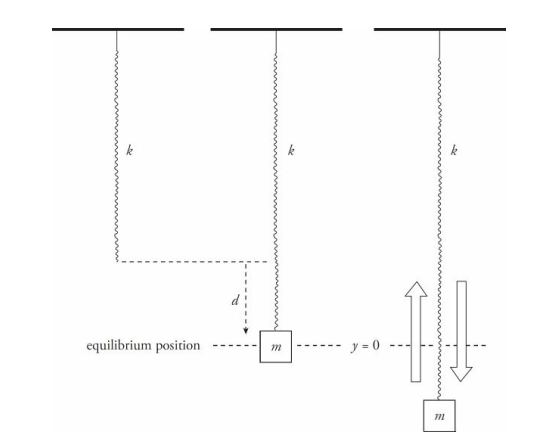
Next, imagine that the block is pulled down a distance A and released.
- The restoring force is greater than the block’s weight, and, as a result, the block accelerates upward.
- As the block’s momentum carries it up through the equilibrium position, FS is less than the block’s weight.
- As a result, the block decelerates, stops, and accelerates downward again, and the up-and-down motion repeats.
When the block is at a distance y below its equilibrium position, the spring is stretched a total distance of d + y, so the upward spring force is equal to k(d + y).
- The downward force stays the same, mg. The net force on the block is
F = k(d + y) – mg - but this equation becomes F = ky, because kd = mg (as we saw above).
- The downward force stays the same, mg. The net force on the block is
Since the resulting force on the block, F = ky, has the form of Hooke’s law, we know that the vertical simple harmonic oscillations of the block have the same characteristics as the horizontal oscillations.
The equilibrium position, y = 0, is not at the spring’s natural length, but at the point where the hanging block is in equilibium.
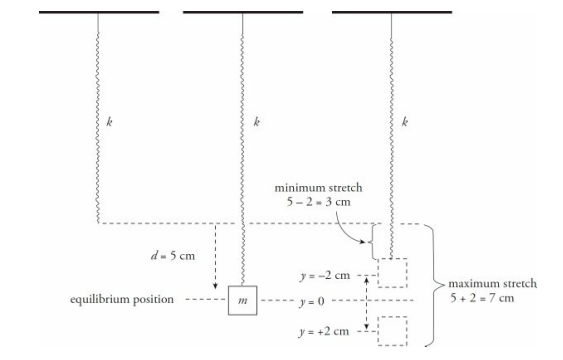
Sample Problem
A block of mass m = 1.5 kg is attached to the end of a vertical spring of force constant k = 300 N/m. After the block comes to rest, it is pulled down a distance of 2.0 cm and released.
(a) What is the frequency of the resulting oscillations? (b) What are the minimum and maximum amounts of stretch of the spring during the oscillations of the block?
Solution
The frequency is given by
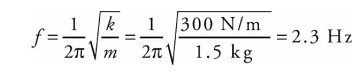
Before the block is pulled down, to begin the oscillations, it stretches the spring by a distance
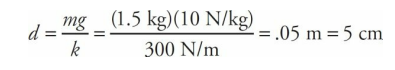
Since the amplitude of the motion is 2 cm, the spring is stretched a maximum of 5 cm + 2 cm = 7 cm when the block is at the lowest position in its cycle, and a minimum of 5 cm – 2 cm = 3 cm when the block is at its highest position.
6.5: The Sinusoidal Description of SHM
The position of the block during its oscillation can be written as a function of time. Take a look at the experimental setup below.
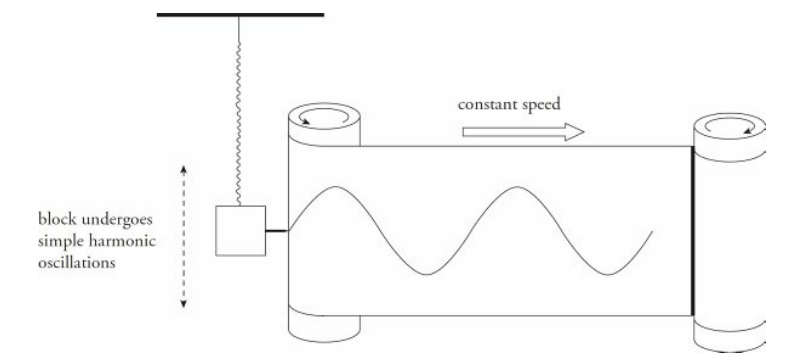
A small pen is attached to the oscillating block, and it makes a mark on the paper as the paper is pulled along by the roller on the right. Clearly, the simple harmonic motion of the block is sinusoidal.
The basic mathematical equation for describing simple harmonic motion is
y = A sin (ωt)- where y is the position of the oscillator, A is the amplitude, ω is the angular frequency (defined as 2πf, where f is the frequency of the oscillations), and t is time.
- Since sin(ωt) oscillates between –1 and +1, the quantity A sin(ωt) oscillates between –A and +A; this describes the oscillation region.
If t = 0, then the quantity A sin (ωt) is also equal to zero. This means that y = 0 at time t = 0. However, what if y ≠ 0 at time t = 0? For example, if the oscillator is pulled to one of its amplitude positions, say y = A, and released at time t = 0, then y = A at t = 0.
To account for the fact that the oscillator can begin anywhere in the oscillation region, the basic equation for the position of the oscillator given above is generalized as follows:
y = A sin (ωt + ϕ0 )where ϕ0 is called the initial phase. The argument of the sine function, ωt + ϕ0 , is called the phase (or phase angle).
By carefully choosing ϕ0 , we can be sure that the equation correctly specifies the oscillator’s position no matter where it may have been at time t = 0. The value of ϕ0 can be calculated from the equation
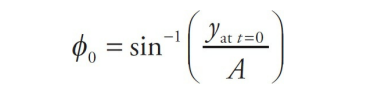
Sample Problem
A simple harmonic oscillator has an amplitude of 3.0 cm and a frequency of 4.0 Hz. At time t = 0, its position is y = 3.0 cm. Where is it at time t = 0.3 s?
Solution
First, A = 3 cm and ω = 2πf = 2π(4.0 s^−1) = 8π s^−1 . The value of the initial phase is
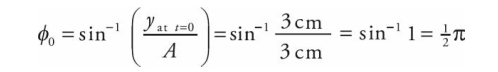
Therefore, the position of the oscillator at any time t is given by the equation
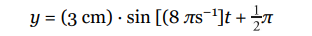
So, at time t = 0.3 s, we find that y = (3 cm) · sin [(8 πs −1) (0.3 s) + π] = 0.93.
Instantaneous Velocity and Acceleration
If the position of a simple harmonic oscillator is given by the equation y = A sin (ω t + ϕ0 ), its velocity and acceleration can be found by differentiation:
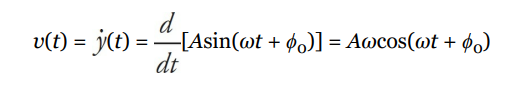
and
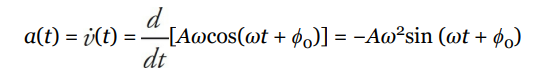
Note that both the velocity and acceleration vary with time
6.6: Pendula
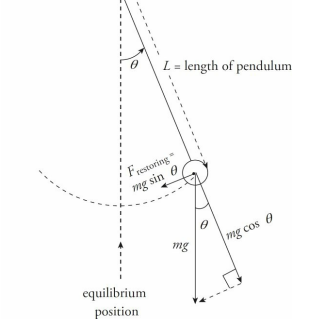
A simple pendulum consists of a weight of mass m attached to a massless rod that swings, without friction, about the vertical equilibrium position.
The restoring force is provided by gravity and, as the figure below shows, the magnitude of the restoring force when the bob is θ to an angle to the vertical is given by the equation:
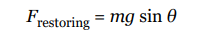
Although the displacement of the pendulum is measured by the angle that it makes with the vertical, rather than by its linear distance from the equilibrium position (as was the case for the spring–block oscillator), the simple pendulum shares many of the important features of the spring–block oscillator.
Displacement is zero at the equilibrium position.
At the endpoints of the oscillation region (where θ = ±θmax ), the restoring force and the tangential acceleration (at) have their greatest magnitudes, the speed of the pendulum is zero, and the potential energy is maximized.
As the pendulum passes through the equilibrium position, its kinetic energy and speed are maximized.
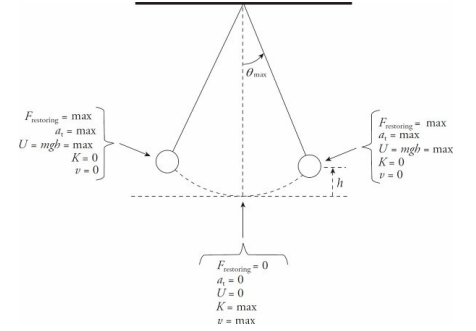
Despite these similarities, there is one important difference. Simple harmonic motion results from a restoring force that has a strength that’s proportional to the displacement. The magnitude of the restoring force on a pendulum is mg sin θ, which is not proportional to the displacement θ. Strictly speaking, then, the motion of a simple pendulum is not really simple harmonic.
- However, if θ is small, then sin θ ≈ θ (measured in radians). So, in this case, the magnitude of the restoring force is approximately mgθ, which is proportional to θ. So if θmax is small, the motion can be treated as simple harmonic.
If the restoring force is given by mgθ, rather than mg sin θ, then the frequency and period of the oscillations depend only on the length of the pendulum and the value of the gravitational acceleration, according to the following equations:
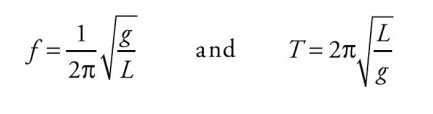
Unit 7: Gravitation
7.1: Gravitational Forces
Kepler’s Laws
- Kepler’s First Law: Every planet moves in an elliptical orbit, with the Sun at one focus.
- Kepler’s Second Law: As a planet moves in its orbit, a line drawn from the Sun to the planet sweeps out equal areas in equal time intervals.
- Kepler’s Third Law: If T is the period, the time required to make one revolution, and a is the length of the semimajor axis of a planet’s orbit, then the ratio T^2/a^3 is the same for all planets orbiting the same star.
Newton's Law of Gravitation
- Proposed by Sir Isaac Newton in 1687
- Describes the force of gravity between two objects
- States that every particle of matter in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them
- Mathematically represented as
F = G * (m1 * m2) / r^2, where F is the force of attraction, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between them - The gravitational constant, G, is a fundamental constant of nature and has a value of approximately
6.674 x 10^-11 N * m^2 / kg^2 - Newton's Law of Gravitation is applicable to all objects in the universe, from the smallest particles to the largest celestial bodies
- It is the basis for understanding the motion of planets, stars, and galaxies
- It was later refined by Albert Einstein's theory of general relativity, which describes gravity as the curvature of spacetime caused by the presence of mass and energy.
Gravitational Potential Energy
- Gravitational potential energy is the energy possessed by an object due to its position in a gravitational field. It is defined as the work done in moving an object from infinity to a point in the gravitational field.
- The formula for gravitational potential energy is:
PE = mgh- where
PEis the potential energy,mis the mass of the object,gis the acceleration due to gravity, andhis the height of the object above a reference point.
- The units of gravitational potential energy are joules (J) in the SI system.
- Gravitational potential energy is an important concept in physics as it helps to explain the behavior of objects in a gravitational field. It is also used in many practical applications, such as in the design of roller coasters and other amusement park rides.
- Gravitational potential energy is a form of potential energy, which means that it can be converted into other forms of energy, such as kinetic energy. The total energy of a system, however, remains constant, according to the law of conservation of energy.
7.2: Orbits of Planets and Satellites
Kepler’s First Law states that the planets’ orbits are ellipses, but the ellipses that the planets in our solar system travel are nearly circular. The deviation of an ellipse from a perfect circle is measured by a parameter called its eccentricity.
The eccentricity, e, is the ratio of c (the distance between the center and either focus) to a, the length of the semimajor axis.
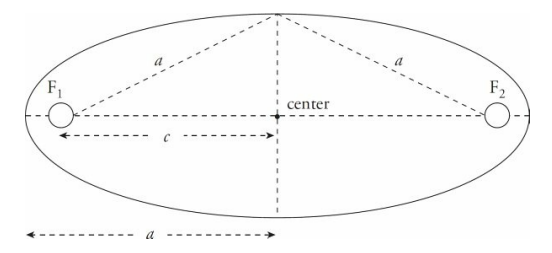
Kepler’s First Law also states that one of the foci of a planet’s elliptical orbit is located at the position of the Sun. Actually, the focus is at the center of mass of the Sun-planet system, because when one body orbits another, both bodies orbit around their center of mass, a point called the barycenter.
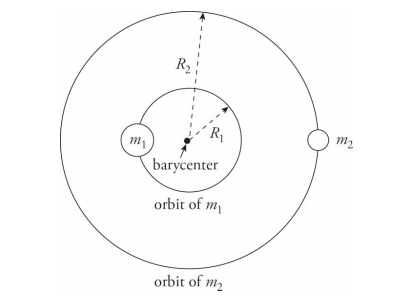
For most of the planets, which are much less massive than the Sun, this correction to Kepler’s First Law has little significance, because the center of mass of the Sun and the planet system is close enough to the Sun’s center.
For example, let’s figure out the center of mass of the Sun-Earth system.
The mass of Earth is m = 5.98 × 10^24 kg, the mass of the Sun is M = 1.99 × 10^30 kg, and the Sun-Earth distance averages R = 1.496 × 10^11 m.
Therefore, letting x = 0 be at the Sun’s center, we have