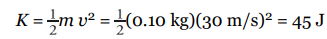3.1: Work-Energy Theorem

Work

• If F is the force, and dr is an infinitesimal amount of displacement, then the work done is: W = ∫F · dr

  • If the force is constant, it can be removed from of the integral, and since F · r = (F cosθ)r for any angle θ, then W = (F cos θ)r. The unit of work is the newton-meter (N·m), which is also called a joule (J).

• Work Sample Problem #1

  You slowly lift a book of mass 2 kg at constant velocity through a distance of 3 m. How much work did you do on the book?

• Solution Problem #1

  • In this case, the force you exert must balance the weight of the book (other-wise the velocity of the book wouldn’t be constant), so F = mg = (2 kg)(10 m/s 2 ) = 20 N.

  • Since this force is straight upward and the displacement, d, of the book is also straight upward, F and d are parallel, so the work done by your lifting force is W = Fd = (20 N) (3 m) = 60 N·m = 60 J.

• Work Sample Problem #2

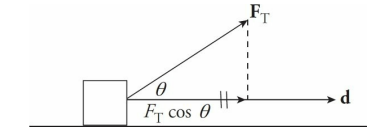
  A 15 kg crate is moved along a horizontal floor by a warehouse worker who’s pulling on it with a rope that makes a 30° angle with the horizontal. The tension in the rope is 200 N and the crate slides a distance of 10 m. How much work is done on the crate by the rope?

• Solution Problem #2

  • The figure below shows that FT and d are not parallel. It’s only the component of the force acting along the direction of motion, FT cos θ, that does work.

    

  • Therefore,

    

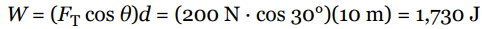
Kinetic Energy

• Kinetic energy is the energy possessed by an object due to its motion. It is a scalar quantity and is dependent on the mass and velocity of the object. The formula for kinetic energy is:

• KE = 1/2 * m * v^2

  • where KE is the kinetic energy, m is the mass of the object, and v is the velocity of the object.

• The SI unit of kinetic energy is joules (J). However, it can also be expressed in other units such as calories, electronvolts, and foot-pounds.

• In a closed system, the total kinetic energy remains constant. This is known as the conservation of kinetic energy. It means that the kinetic energy can be transferred from one object to another, but the total amount of kinetic energy in the system remains the same.

Work Energy Theorem

• The derivation above can be extended to an object with a non-zero initial speed, and the same analysis will show that the total work done on an object—or, equivalently, the work done by the net force—will equal its change in kinetic energy; this is known as the work–energy theorem:

  

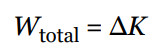
• Work Energy Theorem Sample Problem #1

  What is the kinetic energy of a ball (mass = 0.10 kg) moving with a speed of 30 m/s?

• Solution Problem #1

  • 

• Work Energy Theorem Sample Problem #2

  A tennis ball (mass = 0.06 kg) is hit straight upward with an initial speed of 50 m/s. How high would it go if air resistance were negligible?

• Solution Problem #2

  • This could be done using the Big Five, but let’s try to solve it using the concepts of work and energy. As the ball travels upward, gravity acts on it by doing negative work. [The work is negative because gravity is opposing the upward motion.

    

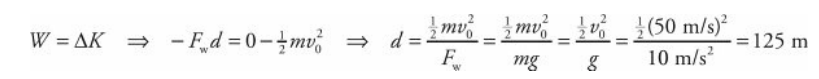
Potential Energy

• Potential energy is the energy possessed by an object due to its position or state. It is the energy that an object has stored within itself, which can be released when the object is allowed to move or change its state.

• Types of Potential Energy

  • Gravitational Potential Energy: It is the energy possessed by an object due to its position in a gravitational field. The higher an object is placed, the greater its gravitational potential energy.

  • Elastic Potential Energy: It is the energy possessed by an object due to its deformation or stretching. The more an object is stretched, the greater its elastic potential energy.

  • Chemical Potential Energy: It is the energy possessed by an object due to the arrangement of its atoms or molecules. The more energy stored in the chemical bonds, the greater the chemical potential energy.

• The formula for potential energy is given by:

  • PE = mgh

  • where PE is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object.

• Potential Energy Sample Problem #1

  A stuntwoman (mass = 60 kg) scales a 40-meter-tall rock face. What is her gravitational potential energy (relative to the ground)?

• Solution Problem #1

  • Calling the ground h = 0, we find

    

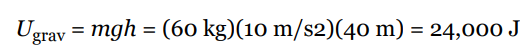
• Potential Energy Sample Problem #2

  If the stuntwoman in the previous example were to jump off the cliff, what would be her final speed as she landed on a large, air-filled cushion lying on the ground?

• Solution Problem #2

  • The gravitational potential energy would be transformed into kinetic energy. So

    

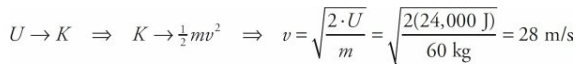
3.2: Conservation of Energy

• The sum of an object’s kinetic and potential energies is called its mechanical energy, E: E = K + U.

• Assuming that no nonconservative forces (friction, for example) act on an object or system while it undergoes some change, then mechanical energy is conserved. That is, the initial mechanical energy, Ei , is equal to the final mechanical energy, Ef , or

  

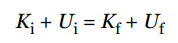
  • This is the simplest form of the Law of Conservation of Total Energy, which we mentioned at the beginning of this section.

Conservation of Energy Sample Problem

A ball of mass 2 kg is dropped from a height of 5.0 m above the floor. Find the speed of the ball as it strikes the floor.

Solution

• Ignoring the friction due to the air, we can apply Conservation of Mechanical Energy. Calling the floor our h = 0 reference level, we write

  

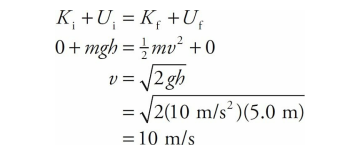
• Note that the ball’s potential energy decreased, while its kinetic energy increased. This is the basic idea behind conservation of mechanical energy: One form of energy decreases while the other increases.

Potential Energy Curves

• Potential energy curves are graphical representations of the potential energy of a system as a function of the distance between two or more particles.

• These curves are used to study the behavior of molecules, atoms, and other particles in a system.

• The shape of the potential energy curve depends on the type of interaction between the particles in the system.

• The potential energy curve for a simple harmonic oscillator is a parabola, while the curve for a diatomic molecule is more complex.

• The potential energy curve for a diatomic molecule has two minima, corresponding to the equilibrium bond length and the dissociation limit.

• The potential energy curve for a polyatomic molecule has many minima and maxima, corresponding to the different conformations of the molecule.

Conservation of Energy Sample Problem

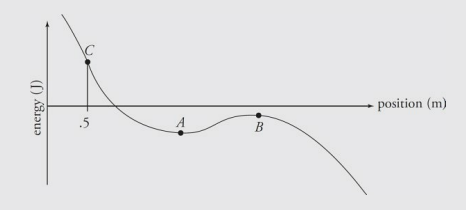
An object of mass m = 4 kg has a potential energy function U(x) = (x – 2) – (2x – 3)^3; Where x is measured in meters and U in joules. The following graph is a sketch of the potential energy function.

(a) Determine the positions of points A and B, the equilibrium points. (b) If the object is released from rest at the point B, can it reach point A or C? Explain. (c) The particle is released from rest at point C. Determine its speed as it passes point A.

Solution

• The points A and B are a local minimum and maximum, respectively, so the derivative of U(x) will be zero at these locations.

  

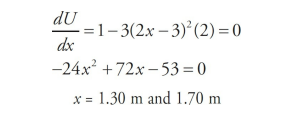
• The object has a negative total amount of mechanical energy at point B because all of its energy is potential energy. It will not be able to reach point C, because that position has a potential energy well above zero.

  • However the object would be able to reach point A because the potential energy at A is less than the energy the object started with at point B. As the object moved from B to A its potential energy would decrease (become more negative) and its kinetic energy would increase.

• First, we need to find how much potential energy the object has at point C, and this will define the total mechanical energy of the object. Then determine the potential energy at point A, x = 1.3 m, and use conservation of energy to determine the speed at point A.

  

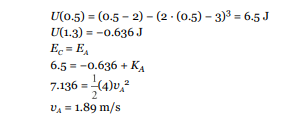
3.3: Power

• Power is the rate at which work gets done (or energy gets transferred, which is the same thing). Suppose you and I each do 1,000 J of work, but I do the work in 2 minutes while you do it in 1 minute. We both did the same amount of work, but you did it more quickly; you were more powerful.

  

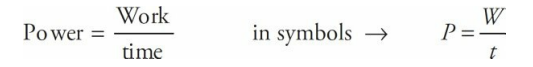
• Since power is a rate, it can be represented as a derivative, too. The calculus (rather than algebra) equation for power is:

  

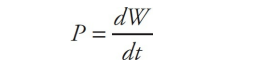
• Power Sample Problem #1

  A mover pushes a large crate (mass m = 75 kg) from the inside of the truck to the back end (a distance of 6 m), exerting a steady push of 300 N. If he moves the crate this distance in 20 s, what is his power output during this time?

• Solution Problem #1

  • The work done on the crate by the mover is W = Fd = (300N)(6 m) = 1,800 J.

  • If this much work is done in 20 s, then the power delivered is P = W/t = (1,800 J)/(20 s) = 90 W.

• Power Sample Problem #2

  What must be the power output of a rocket engine, which moves a 1,000 kg rocket at a constant speed of 8.0 m/s?

• Solution Problem #2

  • The equation P = Fv, with F = mg, yields

    • P = mgv = (1,000 kg)(10 N/kg)(8.0 m/s) = 80,000 W = 80 kW