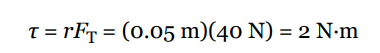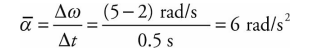Unit 5: Rotation
5.1: Torque and Rotational Inertia
Torque is a measure of the twisting force that causes rotation.
It is defined as the product of force and the perpendicular distance from the axis of rotation to the line of action of the force.
Torque can be calculated using the formula below where T is torque, F is force, r is the moment arm, and theta is the angle between the force and the moment arm.
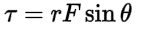
The unit of torque is Newton-meter (Nm) or pound-feet (lb-ft).
Torque is a vector quantity, which means it has both magnitude and direction.
The direction of torque is perpendicular to the plane of rotation and follows the right-hand rule.
Torque is important in many applications, such as engines, motors, and machines.
In engines, torque is used to measure the power output of the engine and is often expressed in horsepower (hp).
Torque can be increased by increasing the force applied or by increasing the distance from the axis of rotation.
The moment arm is the perpendicular distance from the axis of rotation to the line of action of the force and is an important factor in determining torque.
Torque is also related to angular acceleration and moment of inertia, which are important concepts in rotational motion.
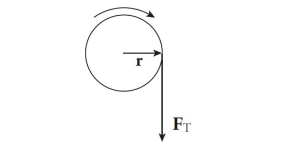
Sample Problem (Torque)
A student pulls down with a force of 40 N on a rope that winds around a pulley of radius 5 cm. What’s the torque of this force?
Therefore, the torque produced by this tension force is simply
Rotational Inertia
- Rotational inertia, also known as moment of inertia, is the property of an object that determines its resistance to rotational motion. It depends on the mass distribution of the object and the axis of rotation.
- The formula for rotational inertia is:
I = ∫ r^2 dm- where I is the rotational inertia, r is the distance from the axis of rotation to the element of mass dm, and the integral is taken over the entire mass of the object.
- The units of rotational inertia are kg m^2.
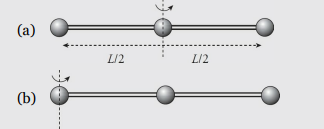
Sample Problem (Rotational Inertia)
Three beads, each of mass m, are arranged along a rod of negligible mass and length L. Figure out the rotational inertia of the assembly when the axis of rotation is through the center bead and when the axis of rotation is through one of the beads on the ends.
Solution
In the first case, both the left bead and the right bead are at a distance of L/2 from the axis of rotation, while the center bead is at distance zero from the axis of rotation. Therefore,
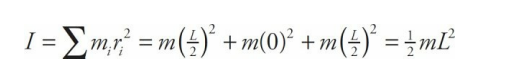
In the second case, the left bead is at distance zero from the rotation axis, the center bead is at distance L/2, and the right bead is at distance L. Therefore,
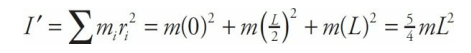
Parallel Axis Theorem
The parallel axis theorem is a principle in physics that relates to the moment of inertia of a rigid body.
- It states that the moment of inertia of a body about any axis parallel to its center of mass is equal to the moment of inertia about the center of mass plus the product of the mass of the body and the square of the distance between the two axes.
The formula for the parallel axis theorem is:
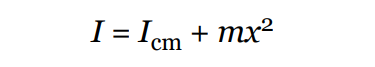
- where I is the moment of inertia about the parallel axis, I_cm is the moment of inertia about the center of mass, m is the mass of the body, and d is the distance between the two axes.
The parallel axis theorem is used in various fields of physics and engineering. Some of its applications are:
- It is used to calculate the moment of inertia of complex objects that cannot be easily calculated using other methods.
- It is used in the design of machines and structures to determine their stability and resistance to rotation.
- It is used in the study of celestial mechanics to calculate the moment of inertia of planets and other celestial bodies.
- It is used in the study of molecular biology to calculate the moment of inertia of molecules and their rotational motion.
The parallel axis theorem is based on certain assumptions and has some limitations. Some of them are:
- It assumes that the body is rigid and does not deform under the applied forces.
- It assumes that the mass of the body is distributed uniformly.
- It assumes that the distance between the two axes is small compared to the size of the body.
- It does not take into account the effects of external forces such as friction and air resistance.
5.2: Rotational Kinematics
Mark several dots along a radius on a disk, and call this radius the reference line. If the disk rotates about its center, we can use the movement of these dots to talk about angular displacement, angular velocity, and angular acceleration.
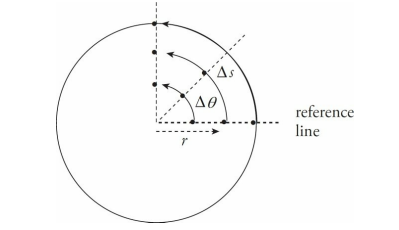
If the disk rotates as a rigid body, then all three dots shown have the same angular displacement, ∆θ. In fact, this is the definition of a rigid body: All points along a radial line always have the same angular displacement.
Just as the time rate-of-change of displacement gives velocity, the time rate-of-change of angular displacement gives angular velocity, denoted by ω (omega). The definition of the average angular velocity is:
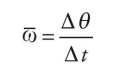
Note that if we let the time interval ∆t approach 0, then the equation above leads to the definition of the instantaneous angular velocity:
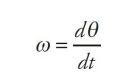
And, finally, just as the time rate-of-change of velocity gives acceleration, the time rate-of-change of angular velocity gives angular acceleration, or α (alpha). The definition of the average angular acceleration is:
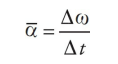
If we let the time interval ∆t approach 0, then the equation above leads to the definition of the instantaneous angular acceleration:
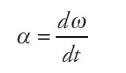
On the rotating disk illustrated on the previous page, we said that all points undergo the same angular displacement in any given time interval; this means that all points on the disk have the same angular velocity, ω, but not all points have the same linear velocity, v. This follows from the definition of radian measure. Expressed in radians, the angular displacement, ∆θ, is related to the arc length, ∆s, by the equation
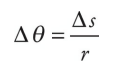
Rearranging this equation and dividing by ∆t, we find that
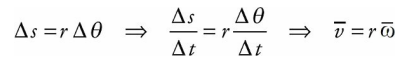
Or, using the equations v = ds/dt and ω = dθ/dt,
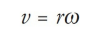
Therefore, the greater the value of r, the greater the value of v. Points on the rotating body farther from the rotation axis move more quickly than those closer to the rotation axis.
From the equation v = rω, we can derive the relationship that connects angular acceleration and linear acceleration. Differentiating both sides with respect to t (holding r constant), gives us
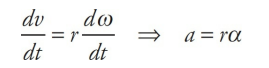
Sample Problem
The angular velocity of a rotating disk increases from 2 rad/s to 5 rad/s in 0.5 s. What’s the disk’s average angular acceleration?
Solution
The Big Five for Rotational Motion
- These five quantities are interrelated by a group of five equations which we call the Big Five. They work in cases in which the angular acceleration is uniform. These equations are identical to the Big Five in Kinematics but, in these cases, the translational variables (s, v, or a) are replaced by the corresponding rotational variables (θ, ω, or α, respectively).
| Equation | Missing Variables | |
|---|---|---|
| Big Five #1 | 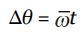 | α |
| Big Five #2 | 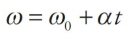 | ∆θ |
| Big Five #3 | 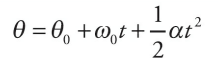 | ω |
| Big Five #4 | 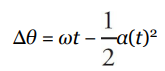 | ω0t |
| Big Five #5 | 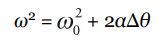 |
5.3: Rotational Dynamics and Energy
Definition of Rotational Kinetic Energy
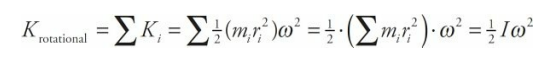
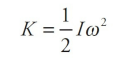
Rolling Motion
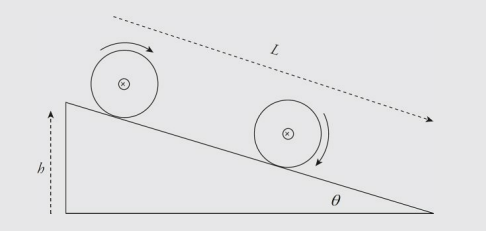
One of the main types of motion associated with rotational motion is rolling motion. We will primarily deal with rolling motion without slipping. Consider a disk rolling down an incline—without slipping:
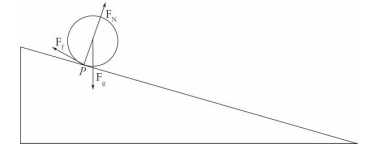
The point of contact of the object with the surface P is instantaneously at rest. If this were not the case, then the disk would be slipping down the incline, so the contact point must not be moving relative to the surface. In this case, the velocity of the center of mass of the disk is equal to the radius times the angular velocity of the disk.
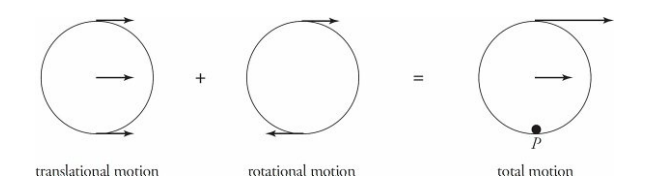
The total motion for an object that is rolling without slipping is the combined motion of the entire object translating with the velocity of the center of mass, and the object rotating about its center of mass, as shown below. This shows the object is instantaneously rotating about the contact point P.
For rolling motion the total kinetic energy is the translational kinetic energy and the rotational kinetic energy.
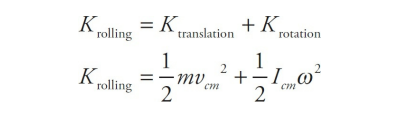
Sample Problem (Rolling Motion)
A cylinder of mass M and radius R rolls (without slipping) down an inclined plane (of height h and length L) whose incline angle with the horizontal is θ. Determine the linear speed of the cylinder’s center of mass when it reaches the bottom of the incline (assuming that it started from rest at the top).
Solution
As the cylinder rolls down the ramp, its initial gravitational potential energy is converted into kinetic energy, which is a combination of translational kinetic energy (since the cylinder’s center of mass is translating down the ramp) and rotational kinetic energy:
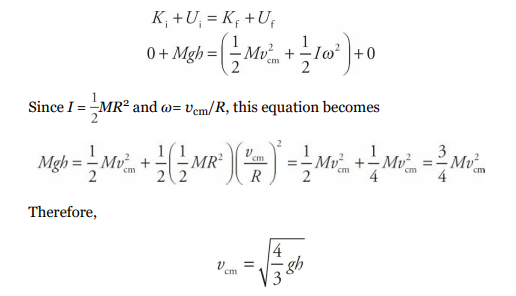
We can verify this result using the result of the previous example. There we found that the acceleration of the cylinder’s center of mass as it rolled down the ramp was a = 2/3gsin θ. Applying Big Five #5 gives us:
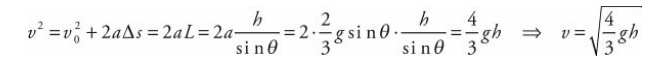
5.4: Angular Momentum
Newton’s Second Law says that
Fnet = dp/dtso if Fnet = 0, then p is constant. This is Conservation of Linear Momentum. The rotational analog of this is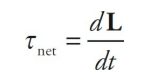
So if τnet = 0, then L is constant. This is Conservation of Angular Momentum. Basically, this says that if the torques on a body balance so that the net torque is zero, then the body’s angular momentum can’t change.
Sample Problem (Angular Momentum)
A child of mass m = 30 kg stands at the edge of a small merry-go-round that’s rotating at a rate of 1 rad/s. The merry-go-round is a disk of radius R = 2.5 m and mass M = 100 kg. If the child walks in toward the center of the disk and stops 0.5 m from the center, what will happen to the angular velocity of the merry-go-round (if friction can be ignored)?
Solution
The child walking toward the center of the merry-go-round does not provide an external torque to the child + disk system, so angular momentum is conserved. Let’s denote the child as a point mass, and consider the following two views of the merry-go-round (looking down from above):
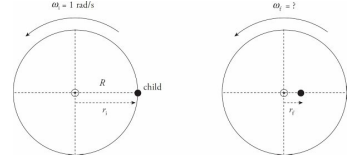
In the first picture, the total rotational inertia, Ii , is equal to the sum of the rotational inertia of the merry-go-round (MGR) and the child:

In the second picture, the total rotational inertia has decreased to
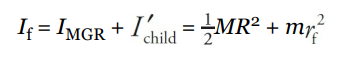
So, by Conservation of Angular Momentum, we have
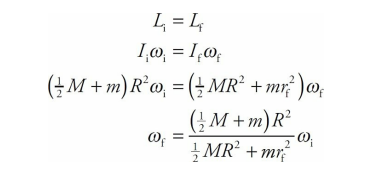
and substituting the given numerical values gives us
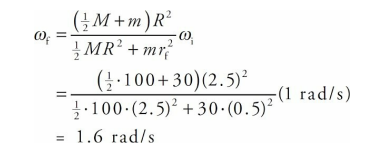
Notice that ω increased as I decreased, just as Conservation of Angular Momentum predicts.
Equilibrium
- Equilibrium in rotational motion occurs when an object is not rotating or is rotating at a constant angular velocity. This means that the net torque acting on the object is zero.
- For an object to be in equilibrium in rotational motion, the following conditions must be met:
- The net torque acting on the object must be zero.
- The object must be at rest or rotating at a constant angular velocity.
- There are two types of equilibrium in rotational motion:
- Static equilibrium: This occurs when an object is at rest and the net torque acting on it is zero.
- Dynamic equilibrium: This occurs when an object is rotating at a constant angular velocity and the net torque acting on it is zero.