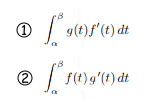Engng Math 145 Parametric equations

Parametric equations

Two variables given as functions of one variable. x = f(t), y = g(t).

Sketching parametric curves

1. Identify the curve

• eliminate parameter to find relationship between x and y

• identities might be needed

2. Determine part of curve that’s included

• use table/knowledge of given parametric eqs

3. Determine direction of curve

• table: sub in t-values to determine (x, y) coordinates

Differentiation with parametric curves

• horizontal tangent when dy/dx = 0

• vertical tangent when dy/dx = undefined

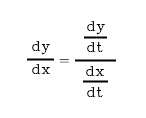
Second derivative of parametric curve

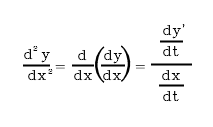
Integration with parametric curves

• For x = f(t) and y = g(t) and boundaries α < t < β

1. Area between curve & x-axis. Integral is negative for below axis.

2. Area between curve & y-axis. Integral is negative for below axis.

If y=a & y=b OR x=a & x=b given then convert to parameter values.

Lower boundary (α) could be bigger than upper boundary (β).