Chapter 2-Central Tendency and Variability

Central tendency

Typical or most representative value of a group of scores

Mean

• Arithmetic average; sum of all the scores divided by the number of scores

• Usually, the best method of measuring central tendency

• Balancing point of a group of scores

Steps for calculating the mean

1. Add up all the scores: ΣX

2. Divide by the number of scores:ΣX/N

Formula for the mean (definitional)

M=ΣX/N

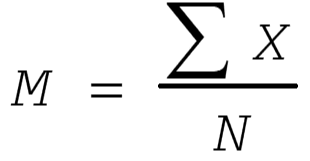
Mode

• most common single number in a distribution; the most frequently occurring value

• Best measure of central tendency for nominal variables

Median

• The middle score, when all scores are arranged from lowest to highest

• Best measure of central tendency for distributions that contain outliers (e.g., income, housing prices)

When describing a nominal variable, the best measure of central tendency to use is the:

Mode

Variance

• The amount of spread of the scores around the mean; how spread out the scores are around the mean

• The average of each score’s squared difference from the mean

Steps for computing the variance:

1. Subtract the mean from each score to get deviation scores: X-M

2. Square each of these deviation scores to get squared deviation scores:(X-M)²

3. Add up the squared deviation scores to get the sum of squared deviation scores (or sum of squares): Σ(X-M)²

4. Divide the sum of squared deviation scores by the number of scores to get variance: Σ(X-M)²/N

Formula for the variance (definitional):

SD²=Σ(X-M)²/N