Biostatistics Midterm

tidyverse

coherent system of packages for data manipulation, exploration, and visualization that share a common design philosophy

The probability of event A is

P(A)

A probability can range from

0 to 1

P(A) can be estimated by

m/n

• n is number of trials or experiments

• m is the number of times A occurs

As n increases

m/n approaches P(A)

Probability

frequency of occurrence of an event

Calculating probability

Numerator: How many times does the event occur 

Denominator: how many times could the event occur

numerator and denominator for a probability of some characteristic

numerator: number of people with that characteristic

denominator: total number of people in the populatio

The complement of event A is 

anything that is NOT

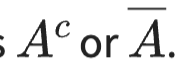
P(A^c)

1-P(A)

Odds

P(A)/P(A^c)

Odds to probability

Joint probability

probability that two separate events both occur

Calculating joint probability

numerator: how many times do both events occur

denominator: how many times could both events occur?

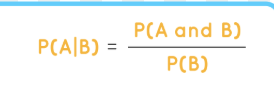
Calculating conditional probability

restrict the sample size to only include those individuals, THEN calculate the probability

count()

used to tally up the number of observations per level of a variable

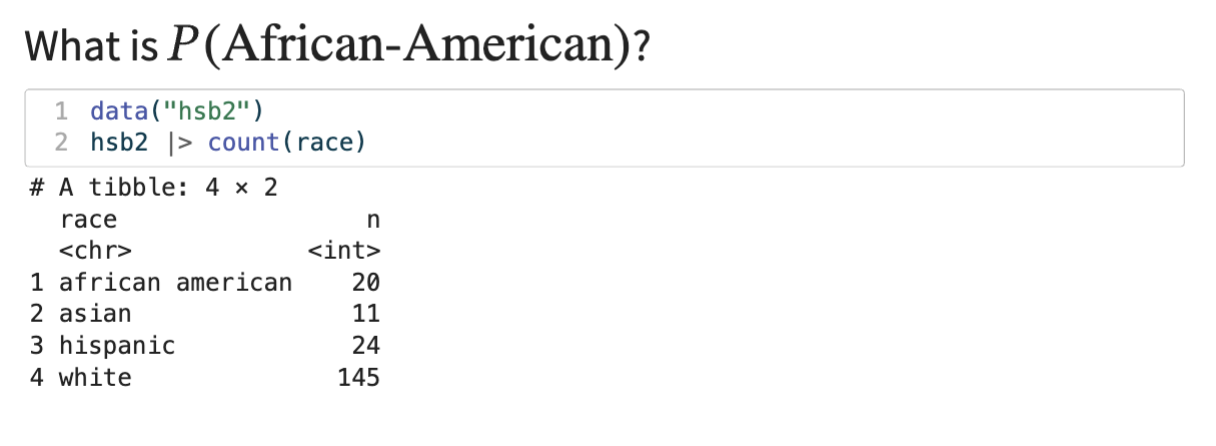
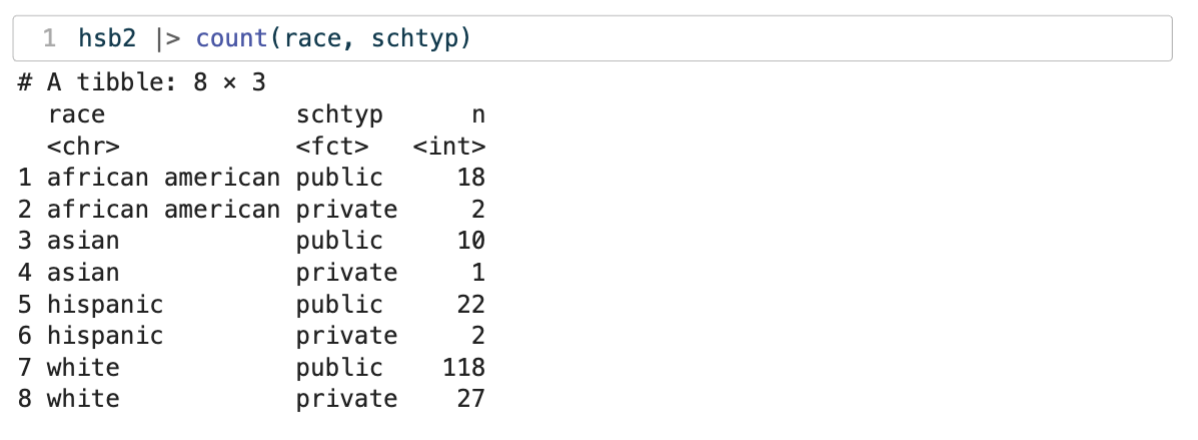
count() and joint probabilities

we cant count() by two variables to get the numbers for a table to calculate joint probabilities

filter()

to get the subset of data we want to condition on

Conditional probability in R

Prevalence

probability of having disease

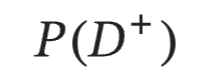
complement of the prevalence

the probability of NOT having disease

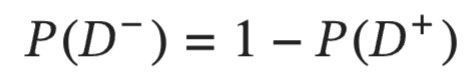
Sensitivity 

conditional probability of testing positive given they have the disease

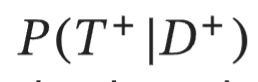
Specificity

conditional probability of testing negative given they do not have the disease

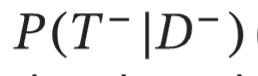
false negative

given a person truly has disease, what is the probability that they test negative?

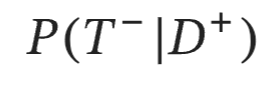
false positive 

given a person truly does not have disease, what is the probability that they test positive?

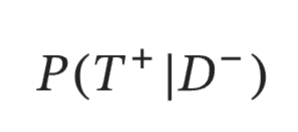
Positive Predictive Value (PPV)

if you test positive, what is the probability you actually have the disease

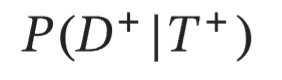
Negative Predictive Value (NPV)

if you test negative, what it the probability that you actually do not have the disease

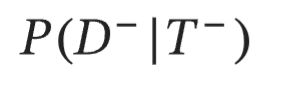
mean

the average 

median

the middle value (50th percentile)

Mode

the most frequent value

na.rm = TRUE

tells R to ignore missing values

calculating mean in R example

Range

the difference between the largest and smallest values

Variance

the average squared-distance each observation is from the mean

standard deviation

measure of how spread out or dispersed the values in a data set are from the mean

standard deviation in R example

parameter

measurement describing the entire population

simple random sample

every member of the population has the same chance of being selected or sampled

Stratified sample

split the population into strata where observations within each strata look similar, then sample from each strata 

cluster sample

split the population into similar clusters full of different looking observations

sample_n()

draws a random sample of size

replace = FALSE

once an observation is selected, it can not be selected again

simple random sample example in R

example of mean in in R

Random variable

an observation that has a single numerical value that is determined by chance, as the outcome

probability distribution

gives the probability of observing any possible value of a random variable

Discrete distributions

a probability distribution that assigns probabilities to a set of distinct, separate, and countable outcomes of a random variable

• ex. number of pets in a household

population proportion

true fraction of individuals in an entire population that share a specific characteristic

basic structure of ggplot

what are all the variables

Continuous Random Variables

can take on any value within a range

• ex. annual radiation exposure level of an x-ray technician

continuous random variable in R

Normal distribution

the most common continuous distribution

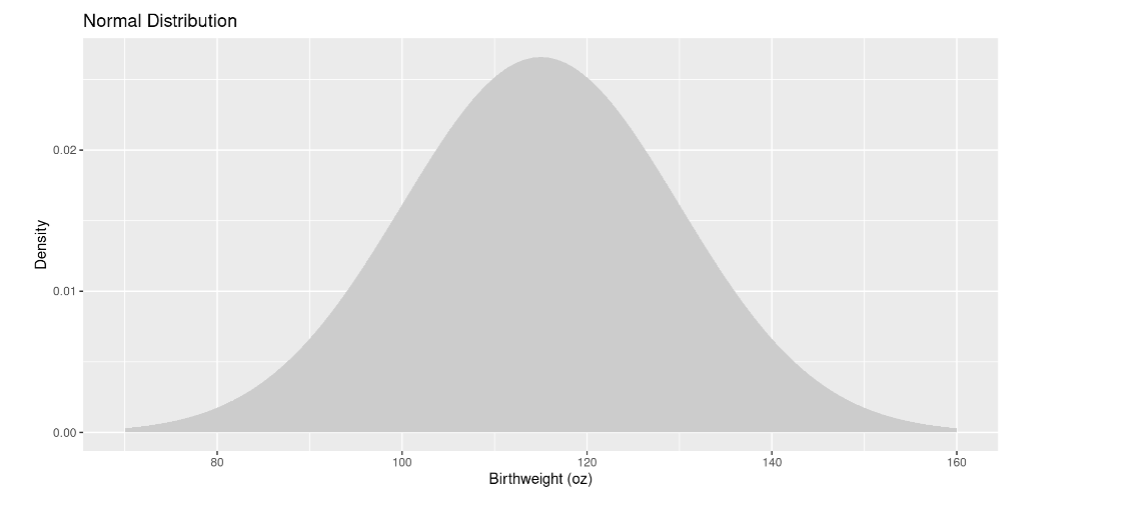
Normal distribution parameters

Mean and standard deviation

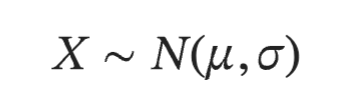
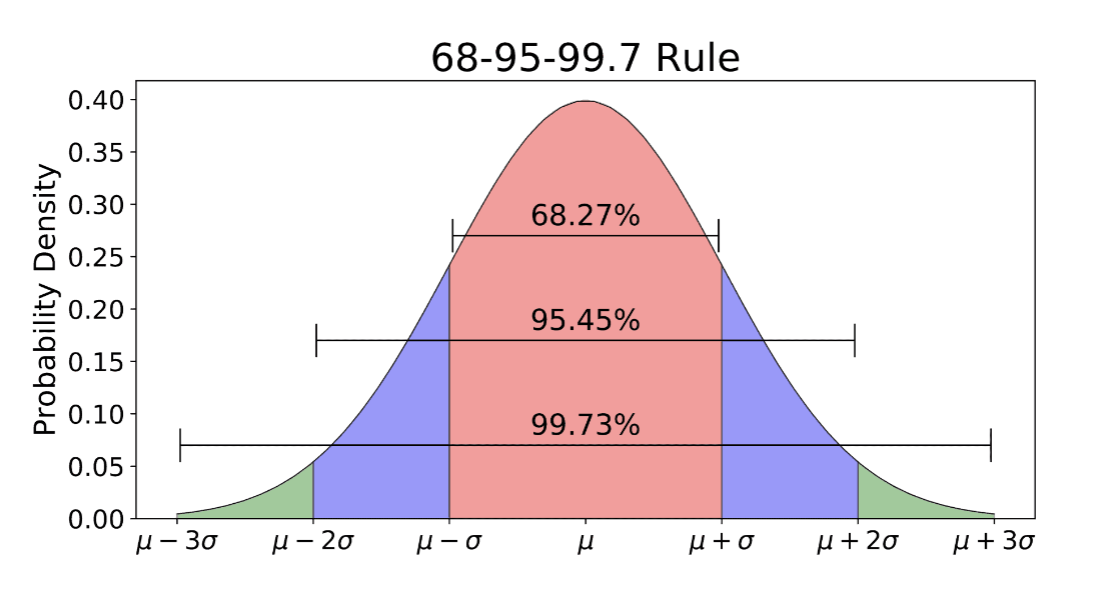
Normal distributions are

symmetric around their mean and unimodal

Normally distributed RVs are

continuous and can take any value from -infinity to infinity

Finding probabilities involved Normal Random Variables

find the area under the curve corresponding to the values we are interested in

areas under normal distributions formula

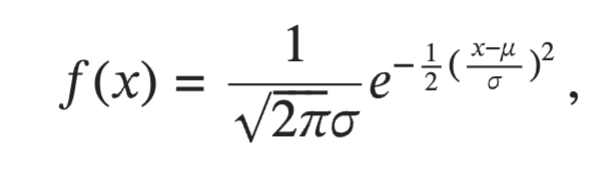
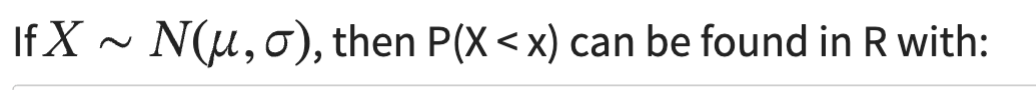
lower.tail = TRUE

tells us we want the probability that is LESS THAN the value we give R (left side of the distribution)

lower.tail = FALSE

tells us we want the probability that is GREATER THAN the value we give R (right side of the distribution)

Normal RVs

qnorm

fine the value that gives you a specific probability

pnorm

find a probability that a normal random variable is less than or greater than a value

Standard Normal Distribution

a special case of the normal distribution with a mean of 0 and a standard deviation of 1, represented by the letter Z

Standardization

normal probability re-written in terms of “how many standard deviations from the mean are we interested in?”

Z score

tells us how many standard deviations away from the mean an observation is