ap calculus bc

instantaneous rate of change

using the closest possible values

average rate of change

between certain bands or subtraction has to equal asked value

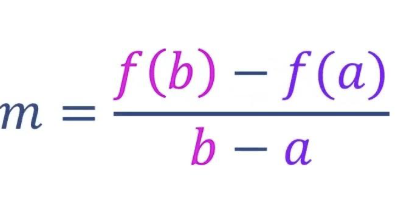
what does limit tell us

what it approaches

not the value

methods for solving limits (6)

direct substitution

algebraically

rationalize

squeeze theorem

graphically

complex functions

complex functions

multiply the denominator to make it easier

squeeze thereom

three types of discontinuity

hole

vertical asymptote

jump discontinuity

which discontinuities are removable and nonremovable

hole → removable

vertical asymptote → nonremovable

jump discontinuity → nonremovable

how to find discontinuities in a function

hole → factor cancels out

vertical asymptote → when the denominator =0

jump is not applicable

three conditions that must be met for continuity

three functions to know that must be restriction on domain

denominator

square roots

logarithms

denominator domain sign

not equal to

square root domain sign

>=

logarithm domain sign

>

hole of function

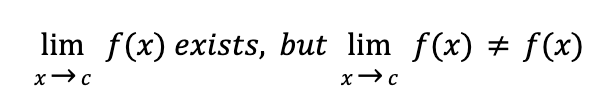
horizontal asymptote

look at the degree

degree is bigger on the bottom → ha is 0

degree is bigger on the top → no ha

degree is equal → cancel and look at constant

basically do the infinite limit

conditions for IVT

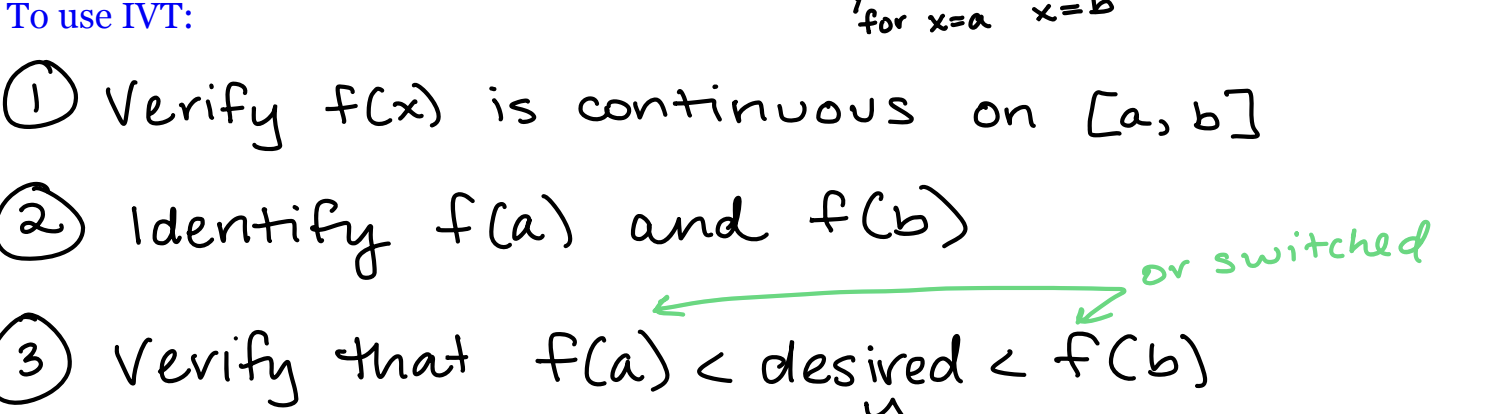
conclusion for IVT

instantaneous rate of change derivative

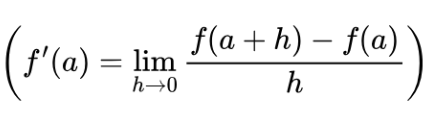
what is the derivative also known as

the slope of the tangent line

equation for the tangent line

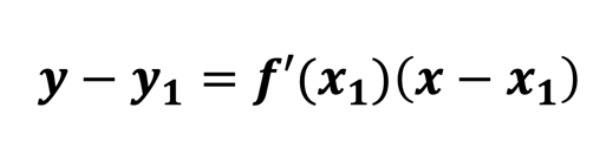
a function is not differentiable when

discontinuous (hole, jump, VA)

corner or cusp

vertical tangent

relationship between differentiability and continuity

differentiability implies continuity but continuity does not imply differentiability (cause can have corner, cusp, vertical tangent)

inverse trig function derivatives (3)

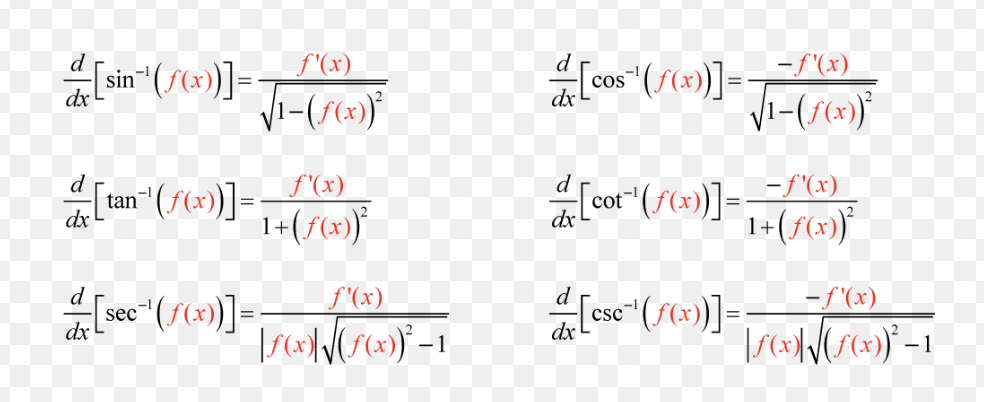
trig inverse domain and range

when does horizontal tangent exist

dy/dx=0

numeration=0 if fraction

when does vertical tangent exist

derivative is undefined

denominator=0 if fraction

derivative of inverse function

normal line

opposite sign reciprocal of slope of tangent line

interpret f’(x)

at x=____, the y-context is changing at a rate of ____ (can be positive or negative with units)

interpreting f’’(x)

at x=_, the rate of change of y-context is changing at a rate of _____ units.

units of f’(x)

units of f(x)/units of x

units of f’’(x)

units of f’(x)/units of x

relationship between position, velocity, and acceleration

position → s(t)

velocity → s’(t)

acceleration → v’(t)=s’’(t)

v(t)>0

moving right, up, forward

v(t)<0

moving left, down, backward

v(t)=0

at rest and possibly changing directions

speeding up

velocity and acceleration same sign

slowing down

velocity and acceleration are opposite sign

concave up tangent line approximatino

under

concave down tangent line approximation

over

l’hopital’s rule

parametric arc length

parametric first derivative

parametric second derivative

arc length

average value for parametrics

slope for vectors

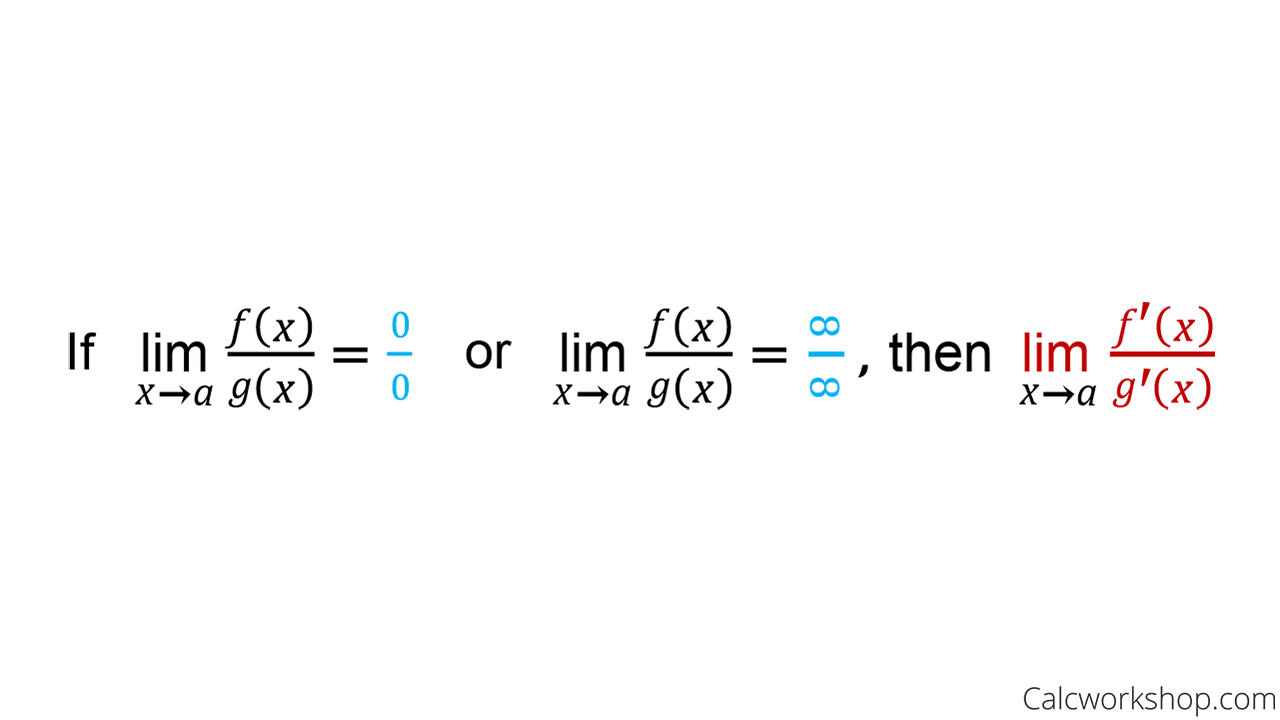
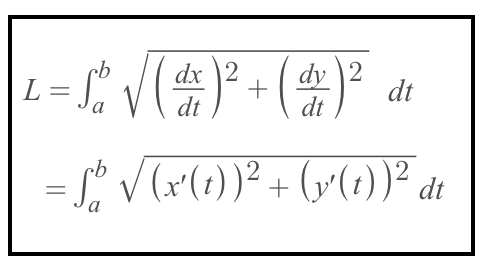
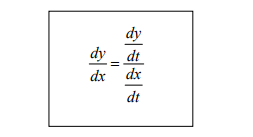
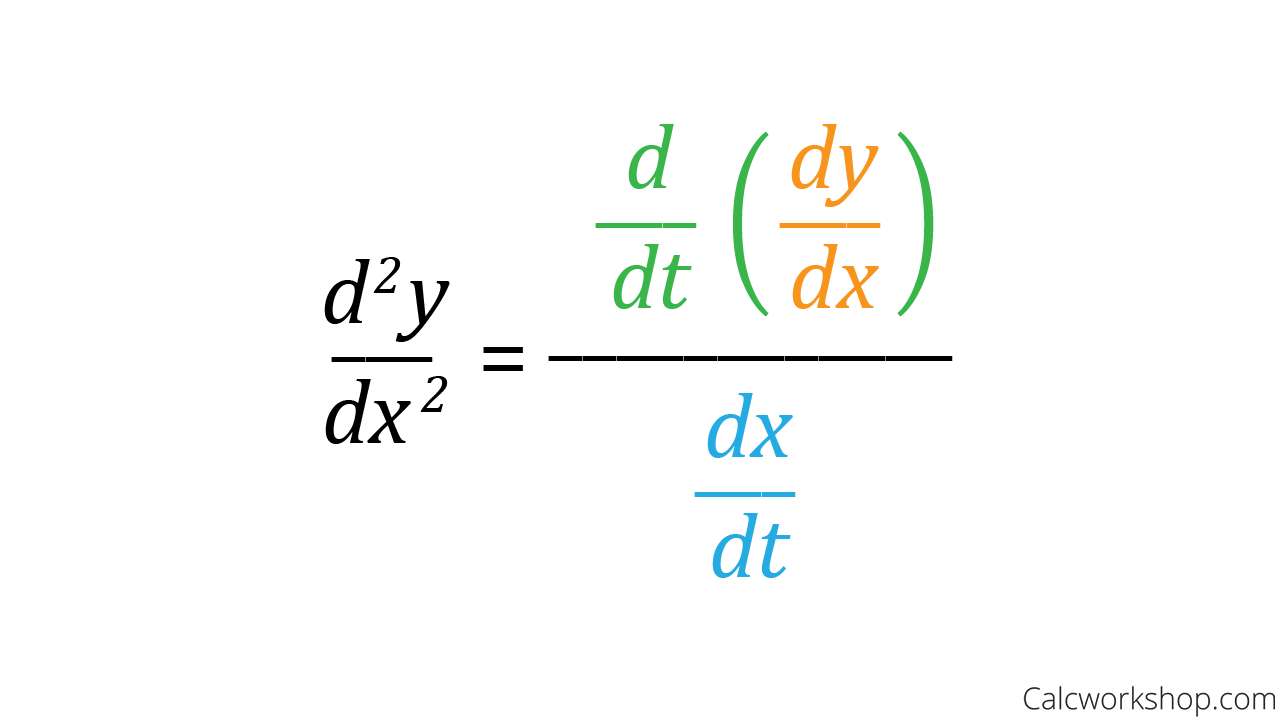
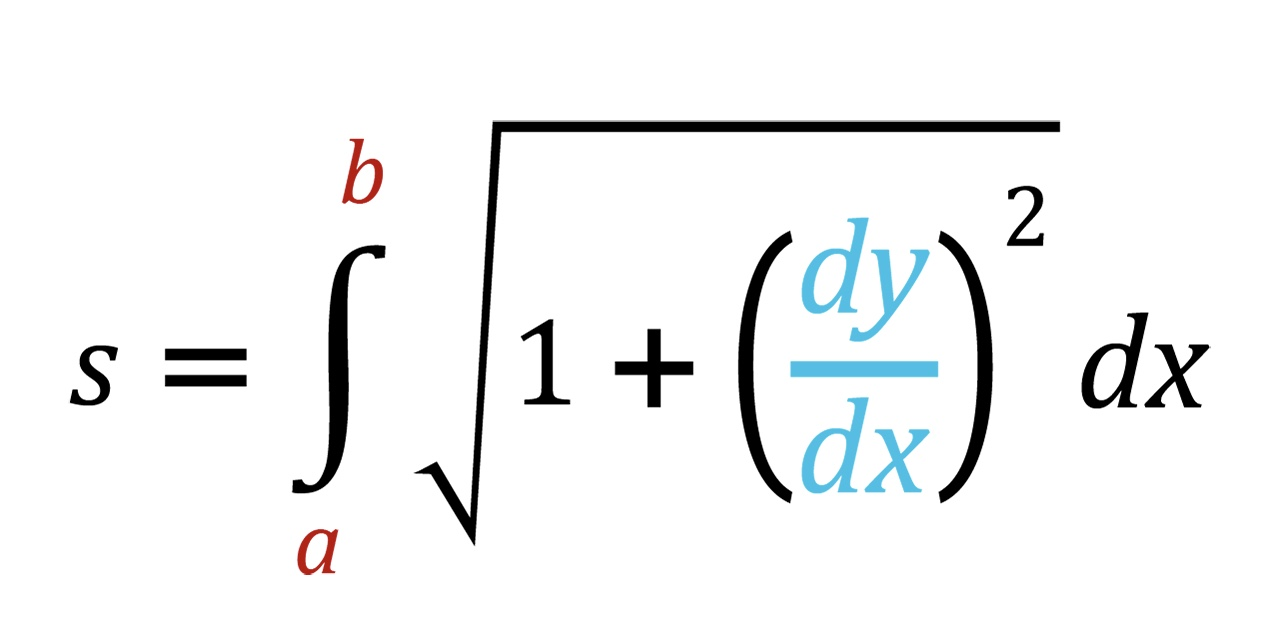
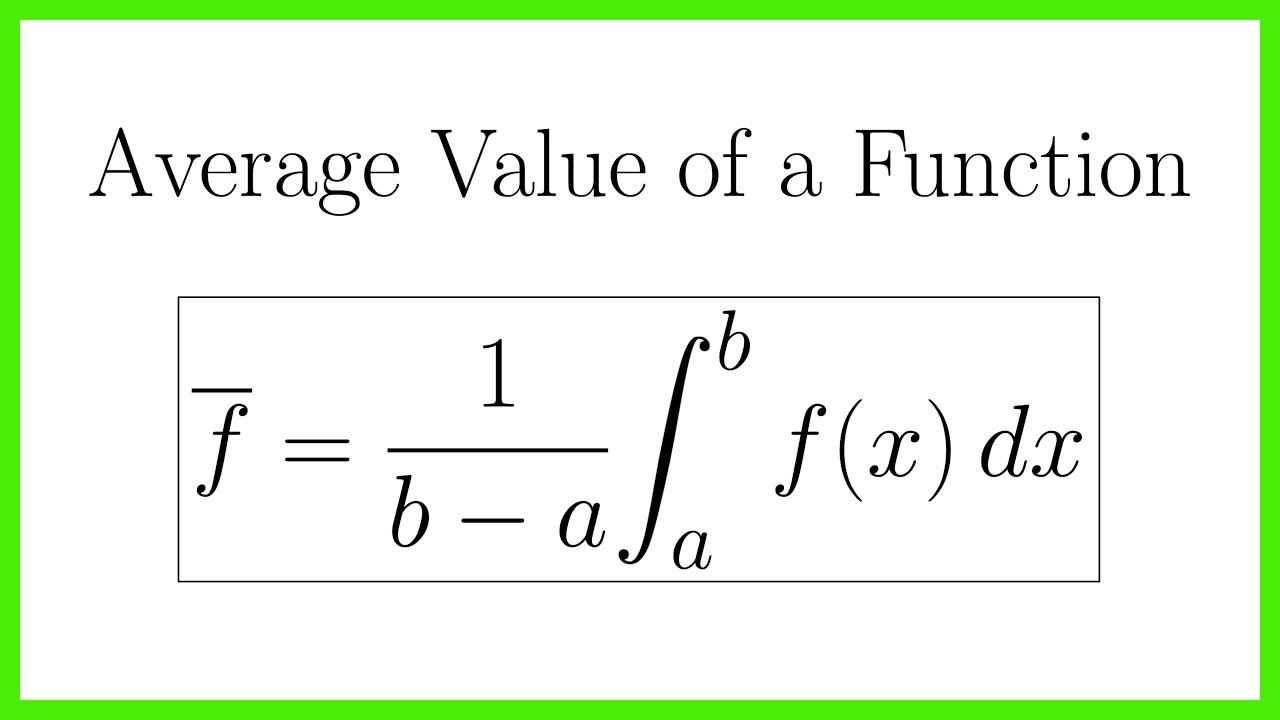
same as parametric

y’(t)/x’(t)

speed

sqrt pythagorean theorem velocity

distance of parametric/vector

each derivative squared and then square root

first derivative polar graphs

second derivative polar graphs

what does it mean if r and dr/dθ are the same sign

moving away from the pole

what does it mean if r and dr/dθ are opposite signs

moving towards the pole

what does it mean if x and dx/dθ are the same sign

moving away from the y-axis

what does it mean if x and dx/dθ are not the same sign

moving towards the y-axis

what does it mean if y and dy/dθ are the same sign

moving away from the x-axis

what does it mean if y and dy/dθ are not the same sign

moving towards the x-axis

antiderivative of cosx

sinx

antiderivative of sinx

-cosx

power rule antiderivative

yk what it is lol

antiderivative of sec²x

tanx

antideriative of secxtanx

secx

antiderivative of csc²x

-cotx

antiderivative of cscxcotx

-cscx

antideriative of e^x

e^x

antiderivative of a^x

antiderivative of 1/x

ln|x|

antiderivative of

arcsinx

antiderivative of

arctanx

format of summation notation for riemann sums

how to determine if over or under approximation with LRAM

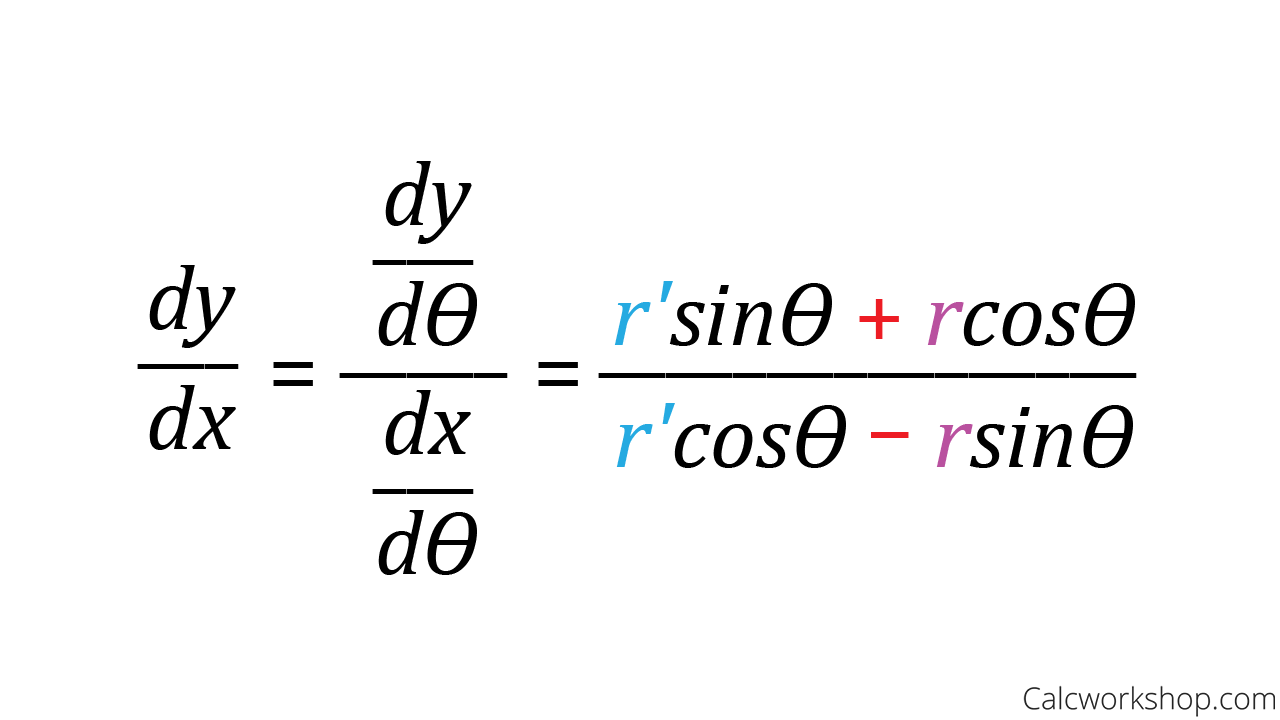
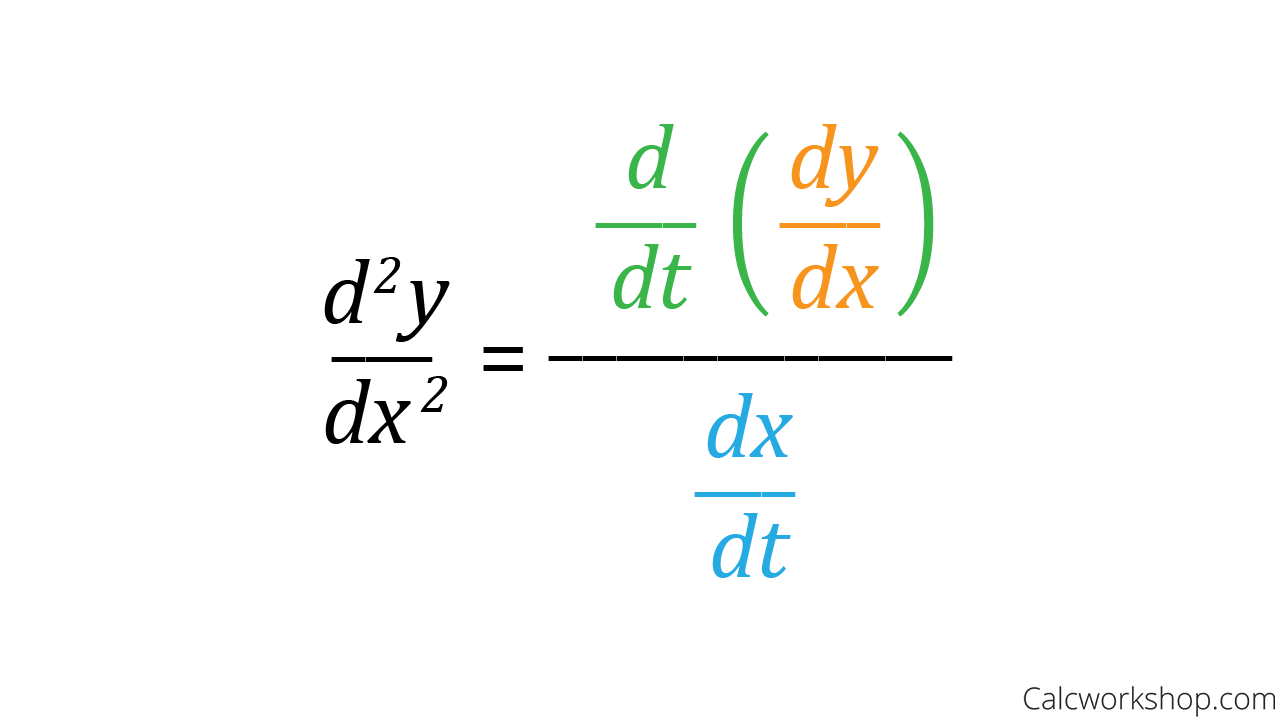
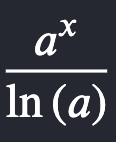
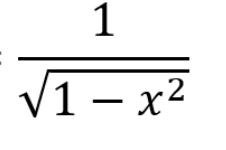
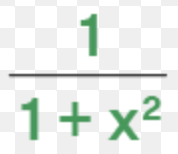
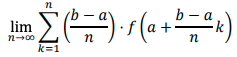
increasing → under

decreasing → over

how to determine if over or under approximation with RRAM

increasing → over

decreasing → under

how to determine if over or under approximation with TRAM

concave up → over

concave down → under

how to interpret distance

between t=____ and t=_____, ______ total _____ is _______ units (nothing is being divided)

how to interpret displacement

between t=___ and t=____, context traveled a displacement of ____ units.

antiderivative of tanx

-ln|cosx|+C