2.01 Use of Symbols

Term

Term

Either 1 of these:

• Number on its own, e.g. 5 (which is 5^1 * x^0)

• Variable on its own, e.g. x (which is 5^0 * x^1)

• Number multiplied by a variable, e.g. 5x (which is 5^1 * x^1)

Terms can include multiple variables and constants, the variables/constants can also be raised to powers greater than 1.

How do we do arithmetic with algebraic expressions?

Algebraic expressions follow the generalized rules of arithmetic.

Algebraic notation

Addition, subtraction, powers/exponents, brackets, follow the same notation as normal numbers during algebraic expressions.

However, for multiplication, no sign is used. E.g: ab means a * b.

For division, fractions are used instead. E.g: a/b means a ➗ b.

Variable

Unknown numerical value in an an expression, equation, formula, or identity, whose value can change. Variables are often represented by letters/symbols. In equations, these symbols represent specific numbers; In expressions, formulas, or identities, these symbols represent variables.

Coefficient

Number (constant) multiplied to the variable.

E.g: in 42x, 42 is the constant while x is the variable; in -18y, -18 is the constant while y is the variable.

Constant

Numbers containing no variables, i.e. numbers multiplied to variables raised to the power of 0.

Factor

Number, value, or algebraic expression that can divide into another number, value, or algebraic expression leaving no remainder. For example all the factors of 4xy are 1, 2, 4, x, 2x, 4x, y, 2y, 4y, xy, 2xy, and 4xy.

Factorize

To write a number, value, or algebraic expression as the product of its factors.

Common factor

Factor that divides with no remainder into 2 numbers, values, or algebraic expressions.

Expression

Algebraic statement that does NOT include an equals sign, there is no stated value equal to the expression which allows us to solve it (because there is nothing to solve).

Expressions are made by arithmetically combining terms (e.g. adding, subtracting, multiplying, or dividing terms). A single term can also be an expression.

Expressions can also be simplified. E.g: x + x + x simplifies into 3x.

Algebraic expression

Expression made from variables and constants along with arithmetic operations, expression comprised of terms arithmetically combined together.

Equation

Algebraic mathematical statement with an equals sign between the left and right hand side to show that their value is equivalent.

Solution

Correct values for the variables in an equation which allow the left hand side and right hand side’s value to be equivalent, there may be 0, 1, multiple, or infinite solutions depending the equation(s).

Formula

Worded rule, definition, or relationship between different variables/quantities written using letters. Formulas on their own cannot be solved, but once substituting numbers to replace variables in formulas, then equations can be formed, which can subsequently be solved.

E.g: “Weight, w, is mass, m, multiplied by gravitational field strength, g. OR w = mg”.

if w = 50N and g = 10N/kg, find m.

w = mg → 50 = 10m → m = 5kg

Identity

An equation or algebraic statement which is always true, no matter what values are substituted for the variable(s). Identities separate the left hand side and right hand side to show their values are always equal with a ≡ sign.

E.g: 18x + 27x ≡ 45x, regardless of what values of x are chosen, so 18x + 27x ≡ 45x is therefore an example of an identity.

Identity VS Equation

Equations only hold true when the value of the variable(s) is/are equal to the solution(s)’ value. E.g: 3x + 5 = 77 only holds true when x = 24. Equations can be solved. Meanwhile, identities are ALWAYS true regardless of what the variable(s) value(s) is/are. You cannot solve identities but can substitute numbers into the identity and still have it remain true. E.g: 3x + 6x ≡ 9x is an identity.

All identities are equations.

Not all equations are identities (some equations are conditional equations).

Conditional equations

Equation where it’s only true that the left hand side and right hand side are equal when the variable(s) are certain values (the solutions).

What types of equations are there?

1. Conditional equations

2. Identities

Example of how identities can be used to write equations in different forms (use equating coefficients method)

Example: Find p and q in 3(x + y) + 2y ≡ px + qy

3x + 3y + 2y ≡ px + qy

3x + 5y ≡ px + qy

p = 3, q = 5

Equating coefficients meaning in the context of identities

Comparing coefficients of the same variables raised to the same power on the left hand side and right hand side of identities. Equating coefficients can simplify complicated algebraic expressions or derive new identities/relationships.

Inequality

Expression comparing 2 non-equal values and which compares the left hand side’s value to the right hand side’s value.

<

Smaller than

≤

Smaller than or equal to

=

Equal to

≥

Greater than or equal to

Greater than

≠

Not equal to

Solutions to inequalities

Solutions to inequalities are usually inequalities themselves. For example: x + 18 < 63 → x < 45

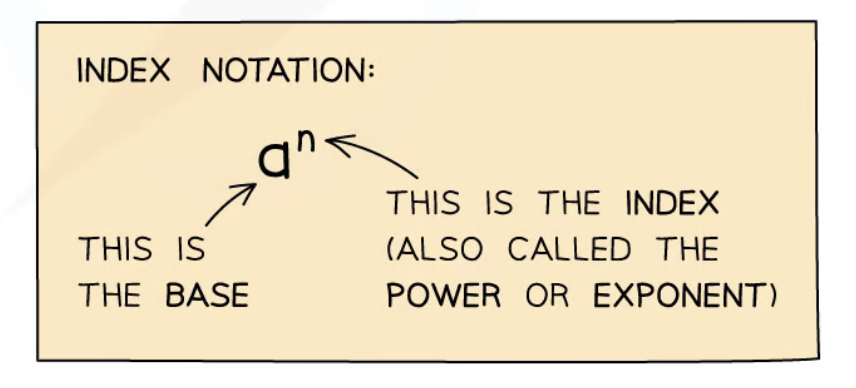
Index notation

Powers/indices/index/exponents are written in the following form:

a^n (better image attached to this flashcard), where a is the base, and n (written in superscript) is the exponent/index. n may be a positive integer, negative integer, fraction, or 0. The same applies to a.

Base

Number that is multiplied repeatedly to itself during exponents. E.g. in 5^18, 5 is the base that is multiplied by itself.

Exponent/indice/power

The number of times that the base is repeatedly multiplied to itself. E.g. in 5^18, 18 is the exponent that shows the base (5) is multiplied to itself 18 times.

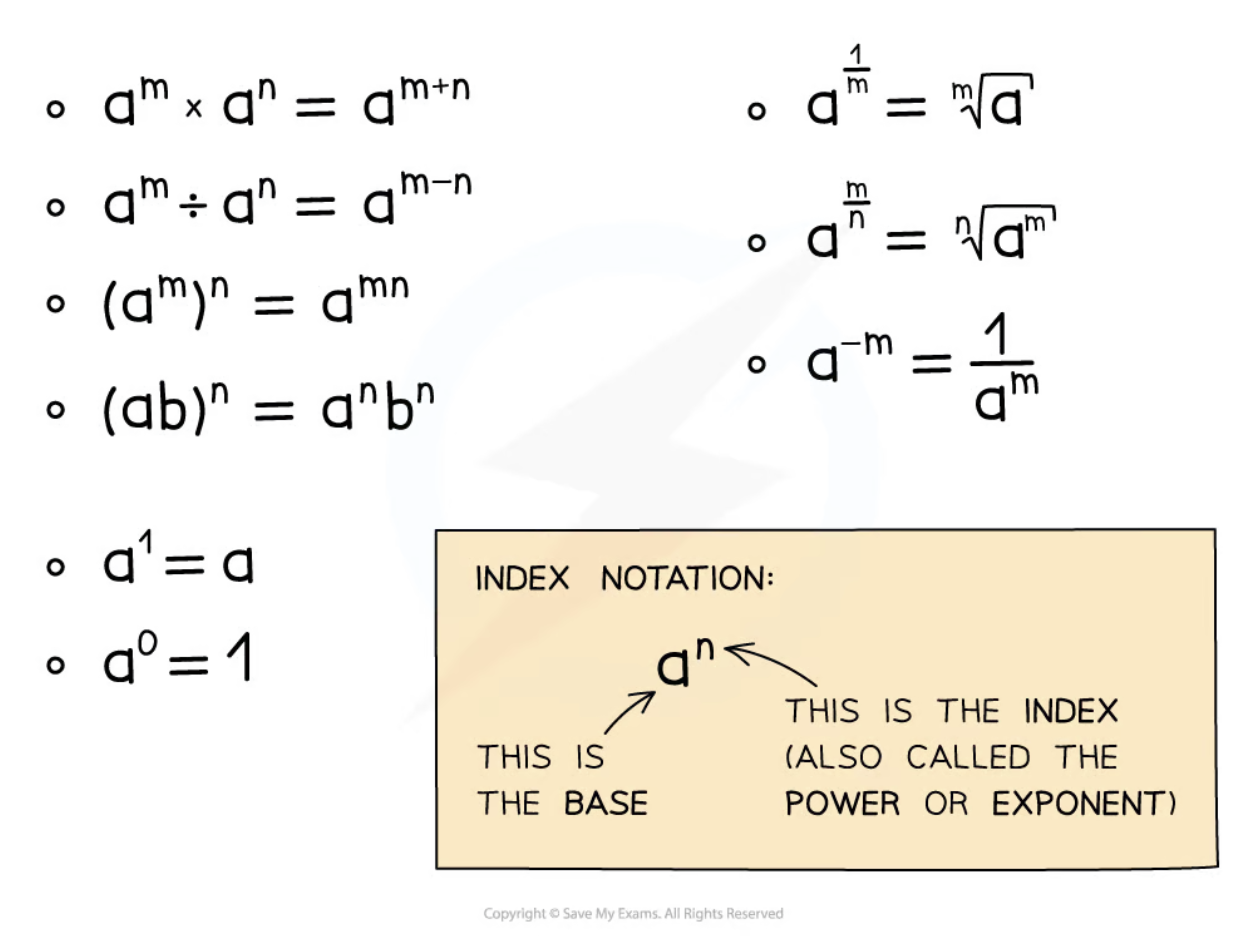
Indices Laws

a^m * a^n = a^(m + n)

a^m ➗ a^n = a^(m - n)

(a^m)^n = a^(mn)

(ab)^n = a^n * b^n

a^(-n) = 1/(a^n)

• a^0 / a^n = 1 / a^n = a^(0 - n) = a^(-n)

a^(1/n) = n √a (nth root of a)

a ^ (m/n) = n √(a^m) (nth root of a to the power of m)

a^1 = a

a^0 = 1 (when a ≠ 0)

• a^n / a^n = 1 = a^(n-n) = a^0

• We cannot divide by 0 to prove that 0^0 is indeed 1, and 0^n is always 0 so this rule does not apply to 0).