Higher Physics Our Dynamic Universe
0.0(0)
0.0(0)
New
Card Sorting
1/90
Earn XP
Description and Tags
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
91 Terms
1
New cards
Scalar
A scalar quantity has only magnitude
2
New cards
Vector
A vector quantity has both magnitude and direction
3
New cards
Scalar quantities
* distance
* speed
* mass
* temperature
* energy
* power
* charge
* speed
* mass
* temperature
* energy
* power
* charge
4
New cards
Vector quantities
* displacement
* velocity
* acceleration
* weight
* force
* friction
* momentum
* impulse
* gravitational field strength
* velocity
* acceleration
* weight
* force
* friction
* momentum
* impulse
* gravitational field strength
5
New cards
What are velocity-time graphs used for?
* To describe the motion of an object in detail
* Calculate the average velocity for a journey
* Calculate distances travelled and resultant displacement
* Calculate values for accelerations and decelerations
* Calculate the average velocity for a journey
* Calculate distances travelled and resultant displacement
* Calculate values for accelerations and decelerations
6
New cards
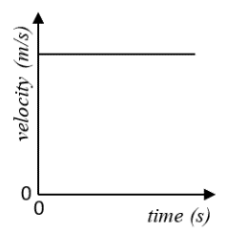
\
Constant velocity
7
New cards
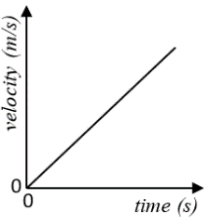
\
Constant positive acceleration
8
New cards
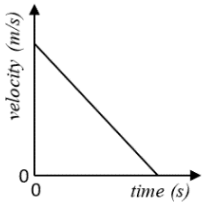
\
Constant negative acceleration
9
New cards
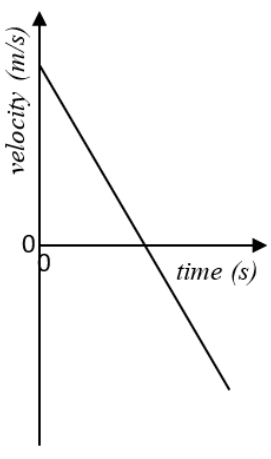
What does this show?
A ball thrown in the air
* decelerates upwards
* then briefly comes to a rest at the top
* then accelerates downwards
* decelerates upwards
* then briefly comes to a rest at the top
* then accelerates downwards
10
New cards
What is the gradient of a graph equal to
The acceleration
11
New cards
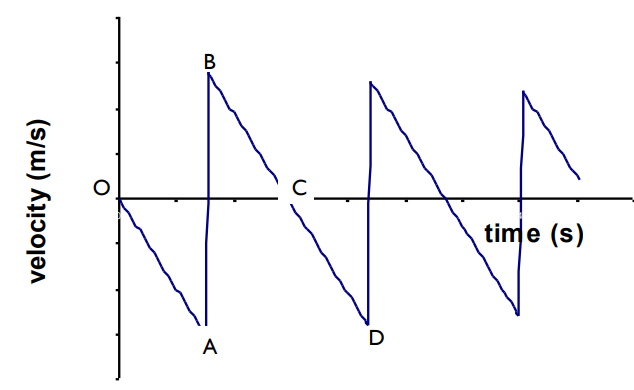
What does this graph show
A ball being dropped from a height and bouncing off the ground with the upwards direction taken as positive and downwards as negative
12
New cards
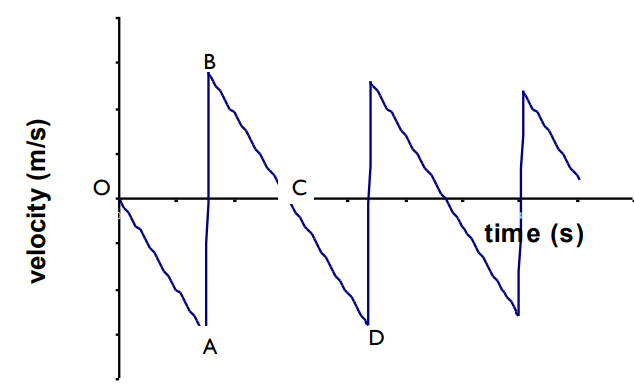
Describe each point on this graph
OA - The ball accelerates towards the ground. The velocity increases in the negative direction.
A - The ball hits the ground
AB - The ball changes direction
B - Leaves the ground
C - Top of flight
CD - The ball travels upwards and decelerates. The velocity decreases in the positive direction
(Process repeats)
A - The ball hits the ground
AB - The ball changes direction
B - Leaves the ground
C - Top of flight
CD - The ball travels upwards and decelerates. The velocity decreases in the positive direction
(Process repeats)
13
New cards
In reality how is energy affected
In reality energy is lost as sound and heat in each bounce, as well as overcoming air resistance when travelling through air.
14
New cards
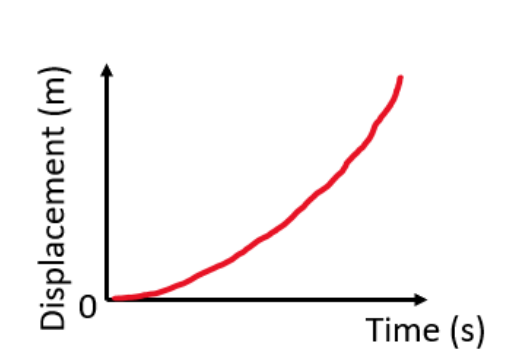
\
Gradient of s-t graph is positive and object covers a larger distance each second (in the same direction)
15
New cards
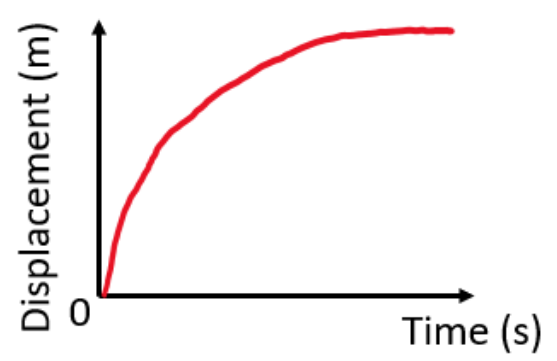
\
Gradient of s-t graph is positive and object covers a smaller distance each second (in the same direction)
16
New cards
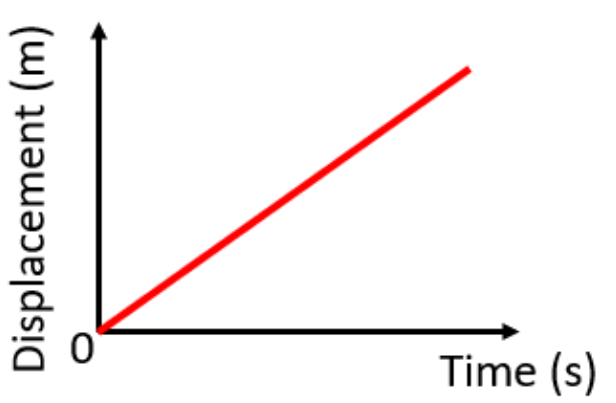
\
Every second the object covers the same distance in the same direction
17
New cards
Acceleration
The rate of change of velocity
18
New cards
Describe the motion of a bouncing ball thrown up in the air
A ball is fired up in the air with a positive velocity. It decelerates upwards to it’s maximum displacement, then accelerates **downwards** due to its weight (a=-9.8ms-2). When it reaches the ground it experiences a large, brief **upward** force which accelerates it upwards until it loses contact with the ground when the acceleration returns to a=-9.8ms-2
19
New cards
Describe motion of a ball dropped from a height
A ball is dropped from a height and falls towards the ground. When it reaches the ground it experiences a large, brief **upward** force which accelerates it upwards until it loses contact with the ground when the acceleration returns to a=-9.8ms-2
20
New cards
Equipment for an acceleration experiment
* cart
* card
* ramp
* ruler
* stopwatch
* light gate
* data logger
* card
* ramp
* ruler
* stopwatch
* light gate
* data logger
21
New cards
Method for acceleration experiment
1. Hold the cart at the top of the slope and release so initial velocity u = 0 ms-1
2. Use a light gate to measure the instantaneous velocity, v, of the card at the bottom of the slope in m/s. You will need to input the length of the card mask into the datalogger which can be measured using a ruler.
3. Measure the time between the cart being released and the light gate at the bottom of the slope using a stopwatch. This is t in seconds.
4. Use a = v-u/t to find acceleration, a, down the slope.
22
New cards
Comments on acceleration experiment
* Repeat the experiment at least 5 times to make the experiment more reliable (by reducing the random uncertainty)
* There will be reading error in the v and t as well as the random uncertainty
* There will be reading error in the v and t as well as the random uncertainty
23
New cards
random uncertainty
max reading - min reading / num of readings
24
New cards
scale reading on analogue scale
\+/- half the least significant division of the scale
25
New cards
scale reading on digital scale
\+/- 1 in the least significant digit displayed
26
New cards
Newton’s 1st law of Motion
An object will remain at rest or constant velocity unless acted on by an unbalanced force
27
New cards
Newton’s 2nd Law of Motion
F=ma
28
New cards
Newton’s 3rd law of Motion
For every action there is an equal and opposite reaction
29
New cards
1 Newton is the unbalanced force which causes a mass of 1kg to accelerate at a rate of 1ms-2
Newton
30
New cards
Fun = ma
Equation for unbalanced force
31
New cards
Apparent W = W
apparent weight in a stationary lift
32
New cards
Apparent W = W
apparent weight in a constant velocity lift
33
New cards
Apparent W > W
\
Apparent W = W + Fun
\
Apparent W = W + Fun
apparent weight in a lift accelerating upwards
34
New cards
Apparent W > W
\
Apparent W = W + Fun
\
Apparent W = W + Fun
apparent weight in a lift decelerating downwards
35
New cards
Apparent W < W
\
Apparent W = W - Fun
\
Apparent W = W - Fun
apparent weight in a lift decelerating upwards
36
New cards
Apparent W < W
\
Apparent W = W - Fun
\
Apparent W = W - Fun
apparent weight in a lift accelerating downwards
37
New cards
Friction is a contact force which opposes motion
Friction
38
New cards
It can be minimized by smoothing surfaces or adding a lubricant such as oil
How can friction be minimized
39
New cards
For an object in free-fall, a constant speed is reached when the upward force on the object (air resistance) is balanced by the downward force on the object (weight)
Terminal velocity
40
New cards
As an object falls it accelerates.
As the speed increases, the air resistance on it will increase.
If it falls for long enough, the air resistance upwards will balance the weight downwards. When forces are balanced the speed is constant. This is the terminal velocity.
As the speed increases, the air resistance on it will increase.
If it falls for long enough, the air resistance upwards will balance the weight downwards. When forces are balanced the speed is constant. This is the terminal velocity.
Describe the process of terminal velocity
41
New cards
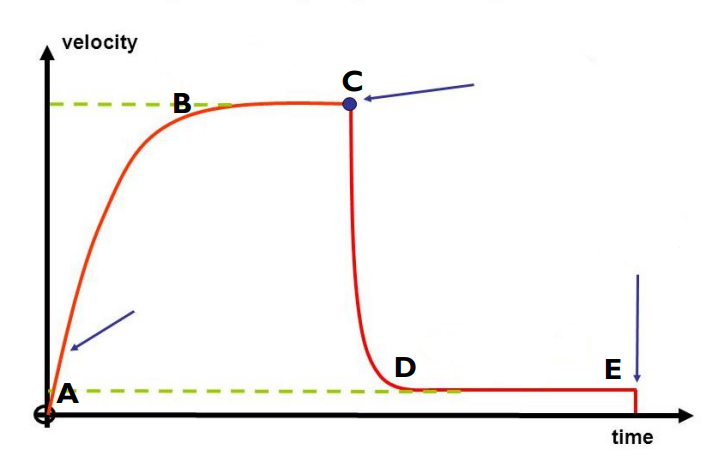
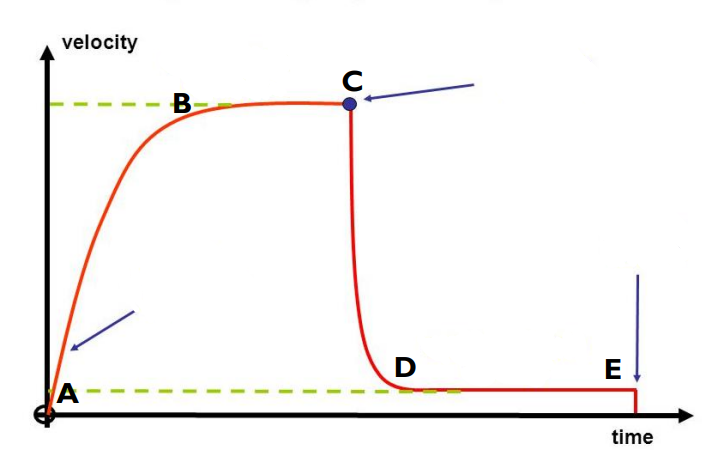
A - initial acceleration = 9.8ms-2
B - first terminal velocity
C - parachute opened
D - second terminal velocity
E - ground reached
B - first terminal velocity
C - parachute opened
D - second terminal velocity
E - ground reached
What happens at each point?
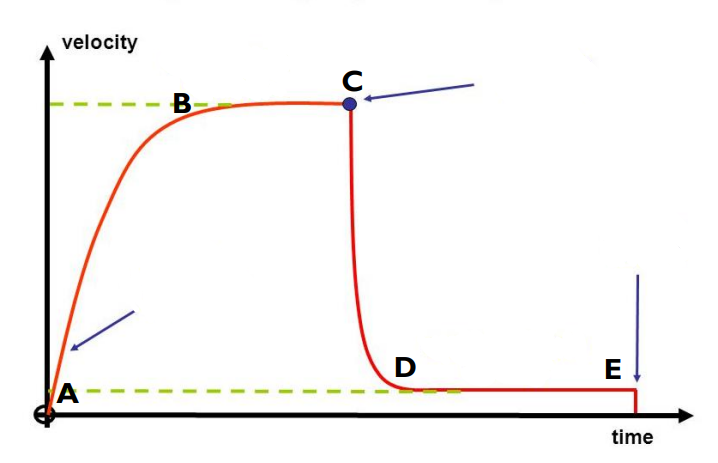
42
New cards
* Increasing velocity with decreasing rate of acceleration
* Initially there is an unbalanced force downwards as weight down is larger than air resistance upwards. As there is an unbalanced force, the object will accelerate as stated by Newton’s 2nd Law
* Initially there is an unbalanced force downwards as weight down is larger than air resistance upwards. As there is an unbalanced force, the object will accelerate as stated by Newton’s 2nd Law
Describe the motion between points A-B
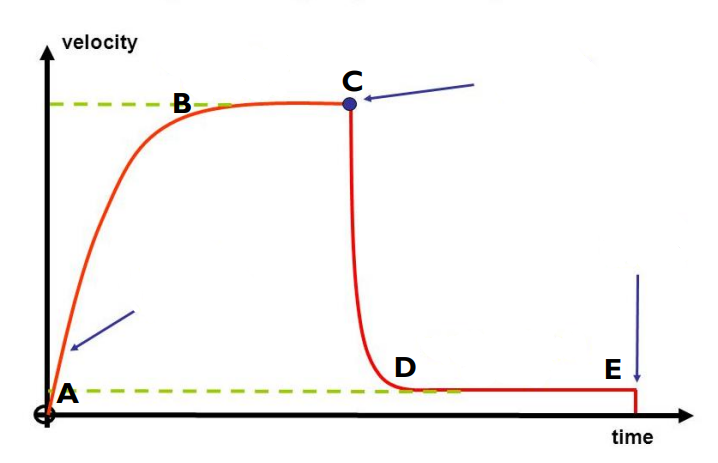
43
New cards
* Terminal velocity
* Forces are balanced so as shown by Newton’s 1st law the object will move with a constant velocity
* Forces are balanced so as shown by Newton’s 1st law the object will move with a constant velocity
Describe the motion between points B-C
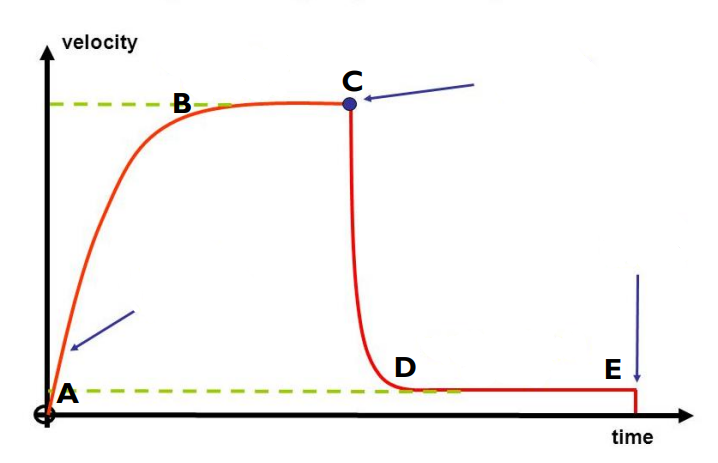
44
New cards
* Sudden decrease in velocity
* Large unbalanced force upwards provided by parachute’s large air resistance
* Large unbalanced force upwards provided by parachute’s large air resistance
Describe the motion at point C
45
New cards
* Second terminal velocity
* Forces are balanced so as shown by Newton’s 1st Law the object will move with a constant velocity
* Forces are balanced so as shown by Newton’s 1st Law the object will move with a constant velocity
Describe the motion between points D-E
46
New cards
Tension is present when an object is being towed or suspended by a rope or coupling
Tension
47
New cards
Fv = Fsinθ
Vertical force at an angle
48
New cards
FH = Fcosθ
Horizontal force at an angle
49
New cards
Fdown_slope = mgsinθ
Force down slope
50
New cards
Energy cannot be created or destroyed, it can only be transformed from one type into another
Conservation of energy
51
New cards
* F unbalanced = rocket thrust - mg - friction
* The weight of the rocket decreases since g decreases as it moves further away from the Earth
* The mass of the rocket decreases as it uses up rocket fuel
* As it moves away from Earth, the friction forces due to air-resistance also decrease
* The weight of the rocket decreases since g decreases as it moves further away from the Earth
* The mass of the rocket decreases as it uses up rocket fuel
* As it moves away from Earth, the friction forces due to air-resistance also decrease
Reasons why as a rocket rises the thrust remains constant but the acceleration increases
52
New cards
If the lift were not fully loaded
Describe a situation where a lift could have an upward acceleration greater than the max value without breaching safety regulations
53
New cards
The momentum, p, of an object is its mass multiplied by its velocity
Momentum
54
New cards
The total momentum of all objects before an interaction is equal to the total momentum of all objects afterwards in the absence of external forces
The Law of Conservation of momentum
55
New cards
Vector, RIGHT IS +, LEFT IS -
Is momentum scalar or vector
56
New cards
0kgms-1
Total momentum before an explosion
57
New cards
No kinetic energy is lost
Elastic collision
58
New cards
Kinetic energy is lost
Inelastic collision
59
New cards
* Newton’s 3rd law states that
* “Every action has an equal and opposite reaction”
* During explosions this tells us that objects will travel in opposite directions with the same applied force.
* This force gives rise to an acceleration in line with F=ma dependent on its mass and then a velocity after the contact.
* An equal and opposite force does not necessarily mean each object will travel at the same speed or have the same momentum, this is dependent on the mass
* “Every action has an equal and opposite reaction”
* During explosions this tells us that objects will travel in opposite directions with the same applied force.
* This force gives rise to an acceleration in line with F=ma dependent on its mass and then a velocity after the contact.
* An equal and opposite force does not necessarily mean each object will travel at the same speed or have the same momentum, this is dependent on the mass
Newton’s Laws to describe collisions
60
New cards
If an object is accelerated by a force F, for a time t, the quantity Ft is known as impulse
Impulse
61
New cards
The concept of impulse is useful in situations where a force is not constant and acts for a short period of time
When is the concept of impulse useful?
62
New cards
The impulse of a force is equal to the area under a force-time graph **and** is equal to the change in momentum of an object involved in the interaction
The impulse of a force is equal to what?
63
New cards
When a human skull is brought suddenly to rest, a force acts upon the brain to change its momentum to zero. Without a helmet this occurs over a very short time interval.
* without helmet F1t1 = ()p1
* with helmet F1t1 = ()p2
But the change in momentum is the same so F1t1 = F2t2
Because the time to come to rest is much longer with a helmet, the average applied force will be much lower meaning less risk of brain damage
* without helmet F1t1 = ()p1
* with helmet F1t1 = ()p2
But the change in momentum is the same so F1t1 = F2t2
Because the time to come to rest is much longer with a helmet, the average applied force will be much lower meaning less risk of brain damage
Explain in terms of impulse why a cycle helmet may reduce brain damage
64
New cards
1. Use a metre stick or measuring tape to measure the height of fall (displacement, s, in metres)
2. Use a stopwatch to measure the time (t), between dropping the ball and it hitting the ground in seconds
3. Ensure the ball is dropped so u = 0 m/s.
4. Use the equation s = ut + 1/2 at^2 to calculate acceleration, a
Experiment 1 to measure the acceleration of a falling object (using a stopwatch and a metre stick)
65
New cards
* The bigger the height the better to reduce impact of reaction time
Improvements for method 1 of measuring acceleration of a falling object
66
New cards
1. Use a metre stick or measuring tape to measure the height between the starting position of ball and the pad below (displacement, s, in metres)
2. Pressing the button on the electronic timer will release the ball (electromagnet turned off) and simultaneously start the timer. When the ball hits the pad below, the timer stops. The difference in these times will be time in seconds (t)
3. The initial velocity (u) is 0m/s
4. Use the equation s = ut + 1/2 at^2 to calculate acceleration, a.
Experiment 2 measuring acceleration of falling object (electronic timer)
67
New cards
A projectile has a constant horizontal velocity and a constant vertical acceleration simultaneously
Projectile
68
New cards
Satellites are in free fall around a planet/star
Satellites
69
New cards
The speed of light in a vacuum is the same for all observers
Speed of light in a vacuum
70
New cards
The clock would appear to run slow as the spacecraft is travelling at a relativistic speed, so time dilation would be experienced
If an observer on a planet was to view a clock onboard the spaceship, state whether it would run fast, slow, or normal compared to a watch on their wrist. Justify.
71
New cards
Length contraction
The length of a fast-moving object appears shorter to a stationary observer, what is this?
72
New cards
The change in observed frequency when a source of sound waves is moving relative to the observer.
Doppler effect
73
New cards
* When moving towards the observer, more waves are received per second and the observed frequency increases
* When moving away, fewer waves are received and so the observed frequency decreases
* When moving away, fewer waves are received and so the observed frequency decreases
Doppler effect moving closer and further
74
New cards
The light from objects moving away from us is shifted to longer wavelength
Redshift
75
New cards
The redshift of a galaxy is the change in wavelength divided by the emitted wavelength
Redshift definition
76
New cards
Hubble and Lemaitre found that the further away a galaxy is from us it recesses at a greater speed
Hubble-Lemaitre Law
77
New cards
The Hubble-Lemaitre Law allows us to estimate the age of the universe.
Can be used as evidence to support the Big Bang Theory through evidence for the expanding universe
Can be used as evidence to support the Big Bang Theory through evidence for the expanding universe
What can Hubble-Lemaitre Law allow us to do
78
New cards
v = Ho d
Equation for Hubble Lemaitre Law
79
New cards
The Hubble data shows that galaxies are moving away from us and the greater the distance from us, the faster they are moving away, i.e. Hubble Lemaitre Law
What does the Hubble data show?
80
New cards
The mass of a galaxy can be calculated if the orbital velocity of its stars around its centre are known
How can the mass of a galaxy be estimated
81
New cards
On closer observation, it does not appear that there is enough “normal matter” to stop galaxies from flying apart. To solve this problem, scientists have proposed that there is an additional type of matter holding galaxies together which cannot be seen - dark matter
Dark Matter
82
New cards
Not only is the universe expanding, but the expansion is accelerating. There is no obvious source of energy to cause this expansion but it has been termed dark energy
Dark Energy
83
New cards
* The temperature of stellar objects is related to the distribution of emitted radiation over a wide range of wavelengths
* The peak wavelength of this distribution is shorter for hotter objects than cooler objects
* Hotter objects emit more radiation per unit surface area per unit time than cooler objects
* The peak wavelength of this distribution is shorter for hotter objects than cooler objects
* Hotter objects emit more radiation per unit surface area per unit time than cooler objects
Temperature of Stellar Objects
84
New cards
The Big Bang Theory is based on the idea that the universe started from an exceptionally hot and dense state around 13.8 billion years ago and has expanded and cooled down over time
The Big Bang Theory
85
New cards
* The redshift of galaxies
* Cosmic Microwave Background Radiation
* Nucleosynthesis
* Olber’s Paradox
* Cosmic Microwave Background Radiation
* Nucleosynthesis
* Olber’s Paradox
Evidence for the Big Bang
86
New cards
The “afterglow” of the Big Bang. This is radiation from the hot early universe whose characteristics closely fit those predicted by the expansion of space
Cosmic Microwave Background Radiation
87
New cards
* CMBR is almost identical no matter where you look
* CMBR comes from every direction of space (isotropic)
* CMBR corresponds to a temperature of around 3K, just a few degrees above absolute zero temperature
* CMBR radiation has a redshift z=1089, indicating that space itself has expanded
* Although CMBR is very low intensity, the universe is filled with it, so its total energy added up makes it the dominant radiation in the universe
* CMBR comes from every direction of space (isotropic)
* CMBR corresponds to a temperature of around 3K, just a few degrees above absolute zero temperature
* CMBR radiation has a redshift z=1089, indicating that space itself has expanded
* Although CMBR is very low intensity, the universe is filled with it, so its total energy added up makes it the dominant radiation in the universe
CMBR features
88
New cards
Abundance of hydrogen and helium which agrees well with the Big Bang Theory
Nucleosynthesis
89
New cards
If the universe contains so many galaxies and stars then why is it dark at night?
The explanation suggests that light from these stars stretched as the universe expanded so it now arrives in the form of invisible infra-red radiation
The explanation suggests that light from these stars stretched as the universe expanded so it now arrives in the form of invisible infra-red radiation
Olber’s Paradox
90
New cards
Two observers moving at a constant speed observe the same laws of Physics
First basic postulate of Special Relativity
91
New cards