5.2 Addition Rule and Complememnts (AND FLASHCARDS WITH HW)

5.) A probability experiment is conducted in which the sample space of the experiment is

S = {11,12,13,14,15,16,17,18,19,20,21,22}, and E ={12,13,14,15,16,17,18}.

Assume each outcome is equally likely.

• List the outcomes in E^c_. Then, find P( E^c )

Part 1:

• The complement of​ E, denoted is all outcomes in the sample space S that are not outcomes in the event E.

  • This means there are some outcomes in S that are not in event E. Those events are E^c (outcomes in the sample space not listed in event E)

• So, E^{c =} {11, 19, 20, 21, 22}

---

Part 2:

• To find P( E^c ), divide the number of outcomes in E^c by the number of outcomes in S.

  • Step 1: Find N( E^c ) _{**number of} E^c

    • N( E^c ) = 5

  • Step 2: Find N(S)

    • N(S) = 12

  • Step 3: Find P( E^c ) and round to three decimal points.

    • P( E^c ) = N( E^c ) / N(S)

      • plug values into the formula —> 5/12

---

Answer:

• P( E^c ) = 0.417

6.) If P(E) = 0.45 and P(F) = 0.60, find P( E and F) if​ P (E or F) = 0.75

Find the probability P( E^c ) if P(E) = 0.32

Formula: P( E^c ) = 1 - P(E)

• 1 - 0.32

• P( E^c ) = 0.68

If P(E) = 0.40, P(E or F) = 0.45, and P(E and F) = 0.20, find P(F)

Use this equation:

• P (E or F) = P(E) + P(F) - P(E and F)

Plug values into equation above ^

• 0.45 = 0.40 + P(F) - 0.20

Isolate P(F) on one side

• 0.45 = 0.40 + P(F) - 0.20

• 0.45 - 0.40 = P(F) - 0.20

• 0.45 - 0.40 + 0.20 = P(F)

Add/Subtract. That value is P(F)

• 0.45 - 0.40 + 0.20 = P(F)

• 0.05 + 0.20 = P(F)

• 0.25 = P(F)

A golf ball is selected at random from a golf bag. If the golf bag contains 4 balls of type​ 1, 6 balls of type​ 2, and 5 balls of type​ 3. Find the probability of the following event: “The golf ball is of type 1 or type 2”

Match with appropriate equation

• “The golf ball is of type 1 or type 2” —> P(E or F) = P(E) + P(F)

Find P(1) and P(2)

• P(E) = N(E) / N(S)

  • P(1) = 4 / 15

    • = 0.26

  • P(2) = 6 / 15

    • = 0.4

Add P(1) and P(2). the sum is the probability of type 1 or 2.

• = 0.26 + 0.4

• = 0.66

10.) The following probability model shows the distribution of injuries of youth baseball​ players, ages 5–​14, according to researchers at SportMedBc. The Probability Model is down below. Complete parts​ (a) through​ (d).

Injury Location	Probability
Head	0.111
Face	0.328
Wrist	0.048
Hand	0.157
Knee/Ankle	0.111
Other	0.245

​(a) Verify that this is a probability model.

(b) What is the probability that a randomly selected baseball injury to a 5-14 year old is to the face or​ wrist?

(c) Interpret the probability you got from (b).

(d) What is the probability that a randomly selected baseball injury to a 5-14 year old is to the head, face, or​ wrist?

(e) Interpret the probability you got from (d).

(f) What is the probability that a randomly selected baseball injury to a 5-14 year old is to something other than the face?

(g) Interpret the probability you got from (f).

(a)​Yes; the probability of all events in the table is greater than or equal to 0 and less than or equal to​ 1, and the sum of the probabilities of all outcomes equals 1.

(b) P (E or F) = P(E) + P(F) —> P (Face or Wrist) = P(0.328) + P(0.048) => 0.376

• Use the Addition Rule for Disjoint Events to find the probability. The rule states that if E and F are disjoint​ (or mutually​ exclusive) events, then P(E or F)=P(E)+P(F)

(c) If 1000 baseball injuries to 5-14 year-olds were randomly​ selected, one would expect about 376 of them to have happened to the face or wrist.

• Review the properties of probabilities and then interpret this probability in the context of the problem. Remember, the more repetitions of an​ experiment, the closer the proportion with which the event occurs will be to the computed​ probability, but the observed proportion will not necessarily equal the probability.​ Also, note that the probability model shows the distribution of injuries by location for youth baseball players aged.

  • People aren’t decimal points. Thus, you must convert the probability into a whole number in order to describe how many people in its accurate unit of measure.

    • 0.375 —> 375

      • found by: (0.375 × 100), or you just drop the ‘ 0. ’ and write the number that follows it.

(d) P (E or F) = P(E) + P(F) —> P (Head or Face or Wrist) = P(0.111) + P(0.328) + P(0.048) =>

• Use the Addition Rule for Disjoint Events to find the probability. The rule states that if E, F, and Gare disjoint​ (or mutually​ exclusive) events, then P(E or F)=P(E)+P(F)+P(G)

(e) If 1000 baseball injuries to 5-14 year-olds were randomly​ selected, one would expect about 487 of them to have happened to the head, face, or wrist.

(f) Im not gonna write it out lol, but the answer is 0.672

• Computed the same way I did in part (d). I added all probabilities the question asks for; that is, each probability in the Model EXCEPT the probability for “Face”

(g) If 1000 baseball injuries to 5-14 year-olds were randomly​ selected, one would expect about 672 of them to have happened to the head, face, or wrist.

11.) In an effort to reduce the number of​ hospital-acquired conditions​ (such as infection resulting from the hospital​ stay), Medicare officials score hospitals on a​ 10-point scale with a lower score representing a better patient track record. The federal government reduces Medicare payments to those hospitals with the worst scores. The following data represent the scores received by a set of Illinois hospitals. Complete parts​ (a) through​ (d).

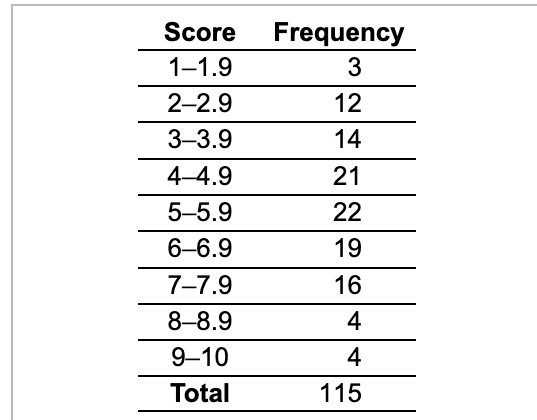
​(a) Determine the probability that a randomly selected hospital in Illinois has a score between 5 and 5.9.

​(b) Determine the probability that a randomly selected hospital in Illinois has a score that is not between 5 and 5.9.

​(c) Determine the probability that a randomly selected hospital in Illinois has a score less than 9.

​(d) Suppose Medicare reduces Medicare payments to any hospital with a score of 8 or higher. What is the probability a randomly selected hospital in Illinois will experience reduced Medicare​ payments? Interpret this result. Is it​ unusual?

(e) Interpret the probability from part (d).

(f) Is the probability from parts (d) and (e) unusual?

(a) 0.191

• If S is the sample space of an​ experiment, then the probability of an event E can be found by using the following​ formula: P(E) = N(E) / N(S) —>

  • where N(E) is the number of outcomes in the event and​ N(S) is the number of outcomes in the sample space.

(b) 0.809

• Use the complement rule. P(E^c ) = 1 - P(E)

  • This is used to find outcomes in a sample spacethat are NOT apart, or asked of, in the event. Using the complement rule for this example would look like 1 - 0.191

(c) 0.965

• identify values of P(E) and N(S)

  • P(E) is P(9 or more)​

• Find what the frequency for ‘9 or more’ is (that is N(E))

• Plug N(E) and N(S) into formula for for P(E)

  • N(E) is 4 and N(S) is 115 —> 4/115 = 0.035

• Next, plug into the complement rule equation:

  • 1 - 0.035

  • = 0.965

(d) 0.070

• P(Events w/ a score of 8 or higher) —> two events, and they both have a frequency of 4.

  • Add the frequencies together and divide by total.

    • 4+4 is 8 —> 8/115

    • = 0.070

(e) If 1000 Illinois hospitals were randomly selected, one would expect approximately 70 of them to experience reduced Medicare payments.

(f) No

• It is not unusual because the probability of experiencing reduced Medicare payments is greater than 0.05

• Addition Rule for probabilities happening at the same time is P (E or F) = P(E) + P(F) - P (E and F).

According to a center for disease​ control, the probability that a randomly selected person has hearing problems is 0.158. The probability that a randomly selected person has vision problems is 0.094. Can we compute the probability of randomly selecting a person who has hearing problems or vision problems by adding these​ probabilities? Why or why​ not?

​A. No, because hearing problems and vision problems are events that are too similar to one another.

B. No, because hearing and vision problems are not mutually exclusive.​ So, some people have both hearing and vision problems. These people would be included twice in the probability.

C.Yes, because hearing and vision are two different​ senses, and​ therefore, they are two unique problems.

D. ​Yes, because this is an application of the Addition Rule for Disjoint Events.

B. No, because hearing and vision problems are not mutually exclusive.​ So, some people have both hearing and vision problems. These people would be included twice in the probability.

• Some people have both hearing and vision problems. This means that the events of having a hearing problem and having a vision problem are not disjoint​ (or not mutually​ exclusive). Remember, when two events are not disjoint the General Addition Rule must be used, where the probability is found by adding together the two given probabilities and subtracting the probability of a person having both problems. If the probability of a person having both problems is not subtracted​ out, then these people will be included twice in the probability.