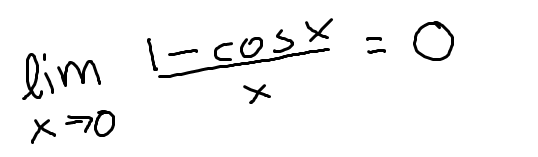BC Calc Things to Memorize - All Units

Formulas and concepts to memorize for the AP Calc BC exam. For more detailed integration flash cards, see my BC Calc Things to Memorize Unit 6 study set.

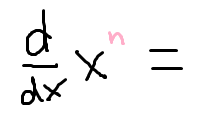
Power Rule

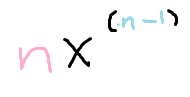
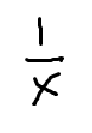
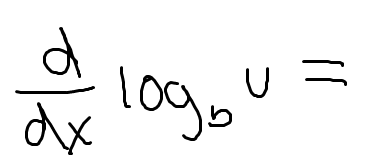
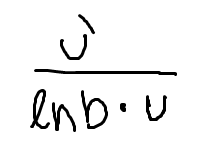
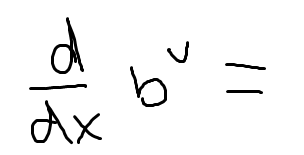
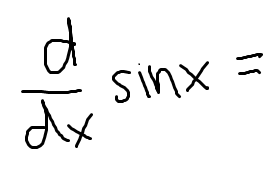
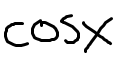
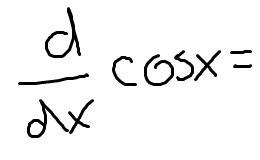
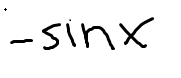
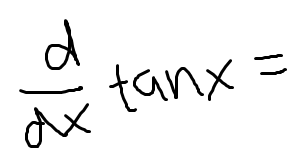
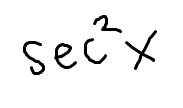
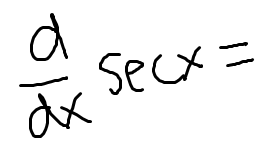
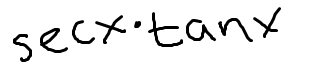
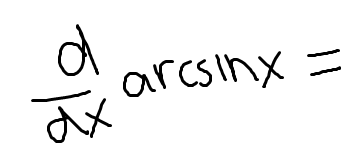
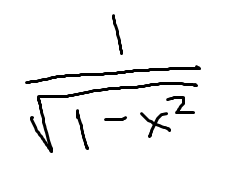
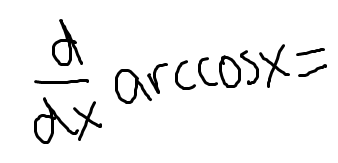
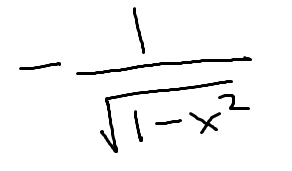
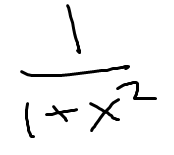
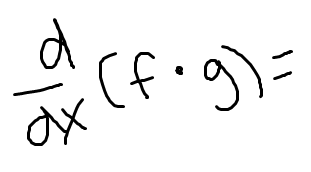
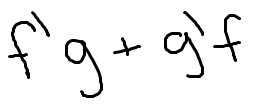
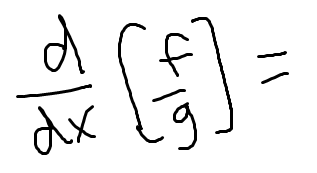
Low D high minus high D low, draw the line and square it below

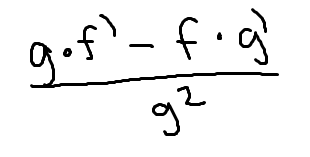
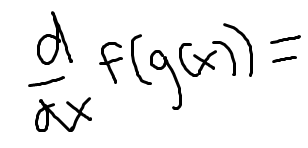
Derivative of the outside function times the derivative of the inside function

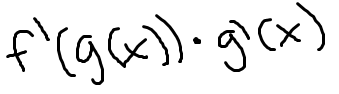
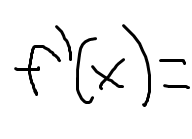
Definition of derivative

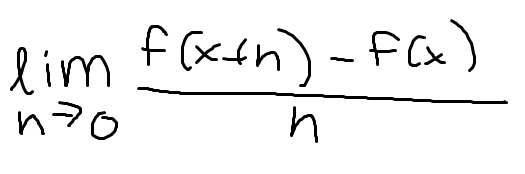
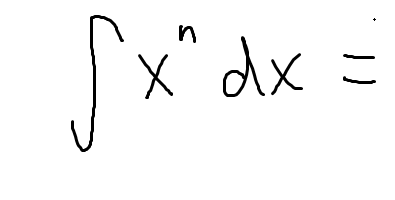
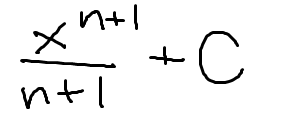
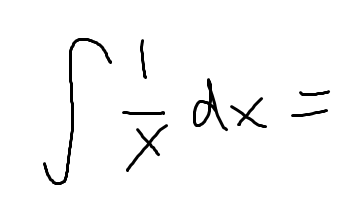
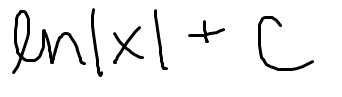
Integration by parts

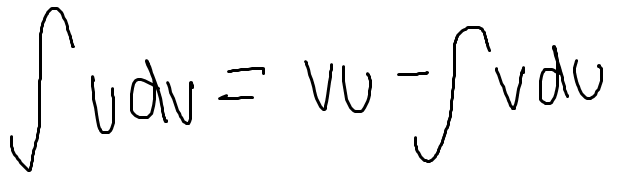
L’Hopital’s Rule

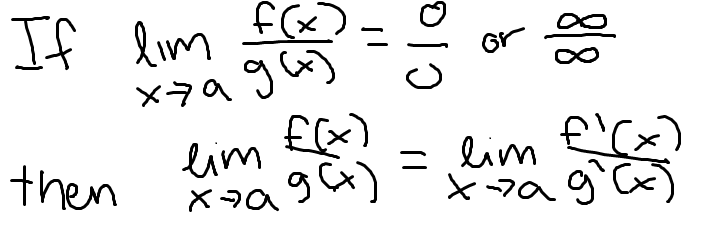
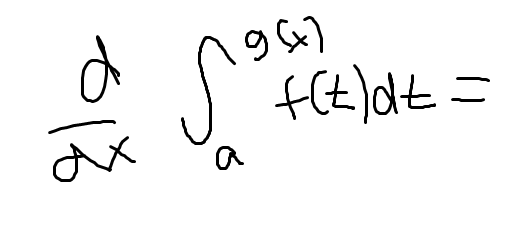
First fundamental theorem

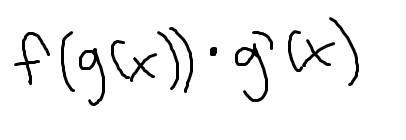
Second fundamental theorem

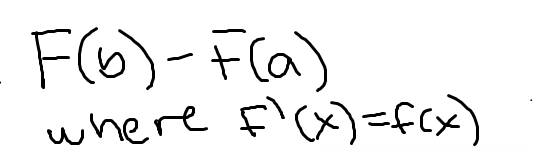
Alternating series error bound

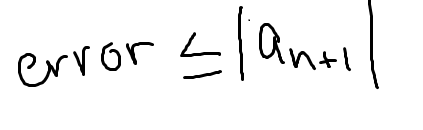
Lagrange error bound

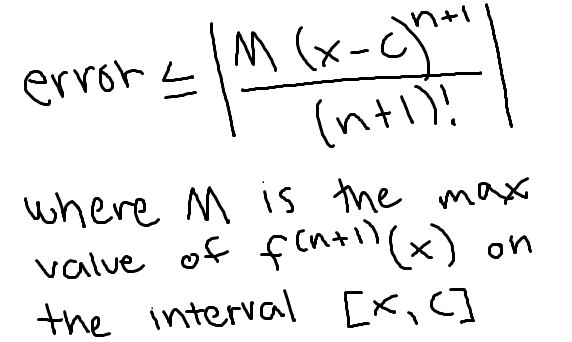
McLaurin series for e^x

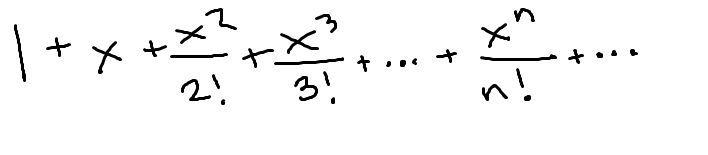
McLaurin series for sin(x)

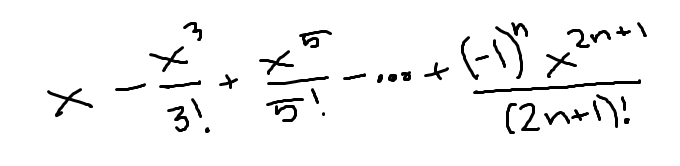
McLaurin series for cos(x)

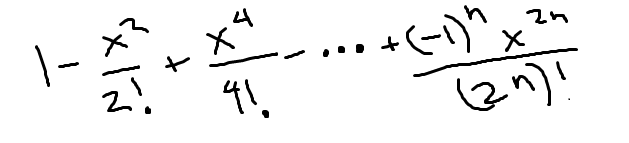
Taylor series centered at x=a

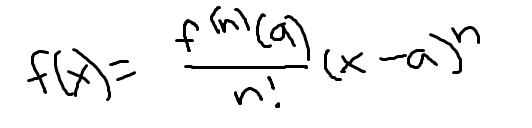
Logistic differential equation

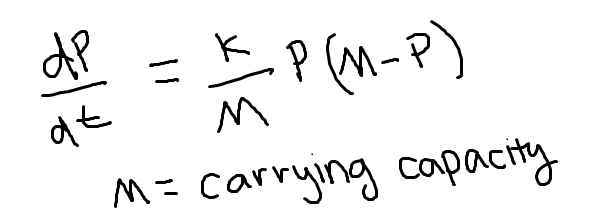
Logistic equation

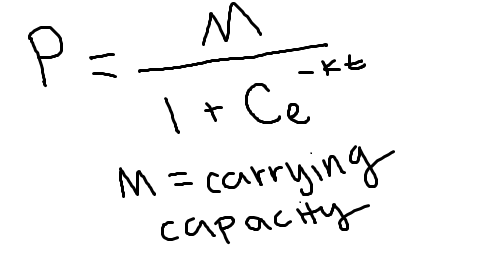
Rolles Theorem

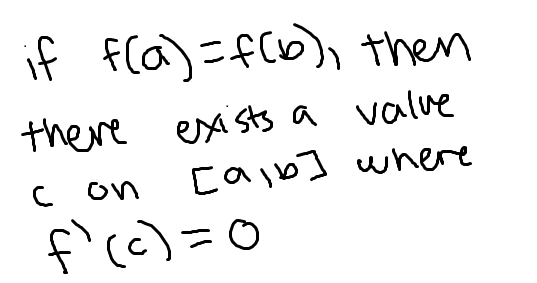
Average value of a function

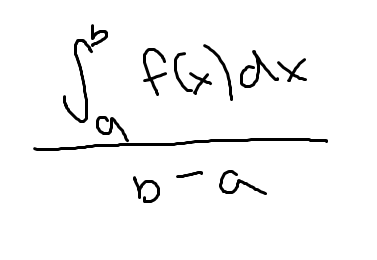
Mean Value Theorem

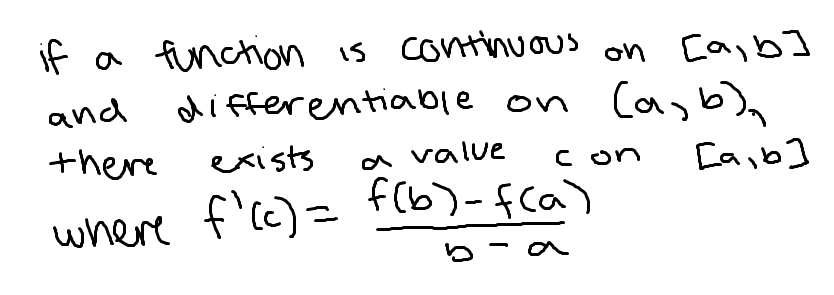
Intermediate value theorem

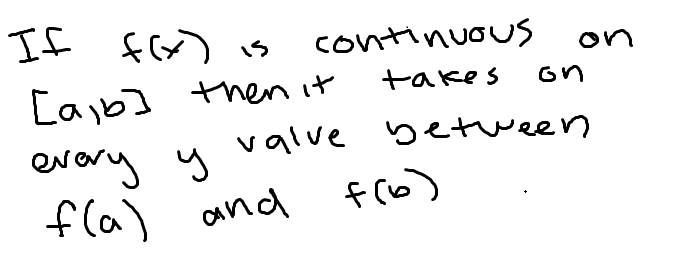
Arc length (cartesian function)

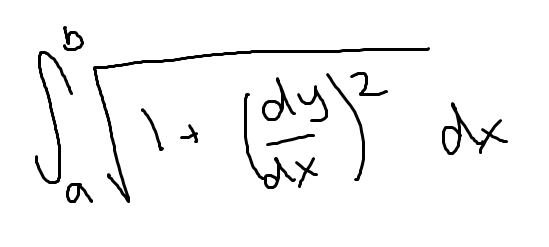
Arc length (parametric function)

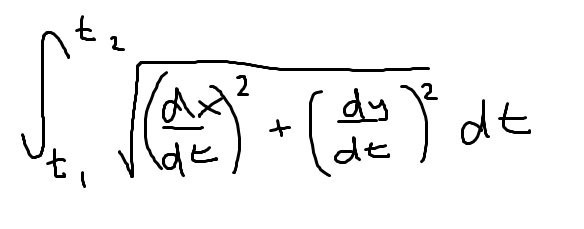
Speed (parametric function)

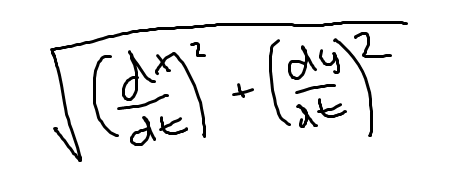
Polar area

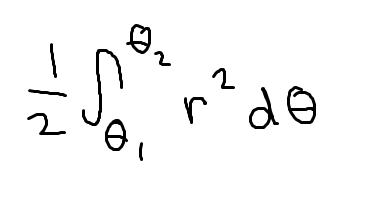
First derivative of a parametric function

note: this is the same for polars, just with theta instead of t

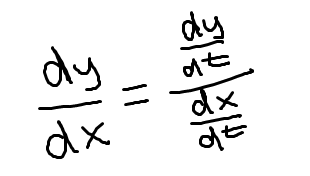
Second derivative of a parametric function

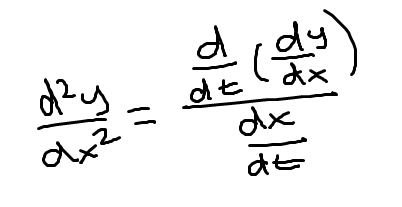
Polar conversions

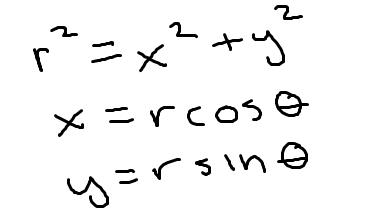
nth term test

Cannot be used to prove convergence

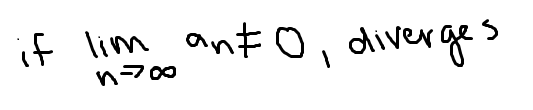
geometric series test

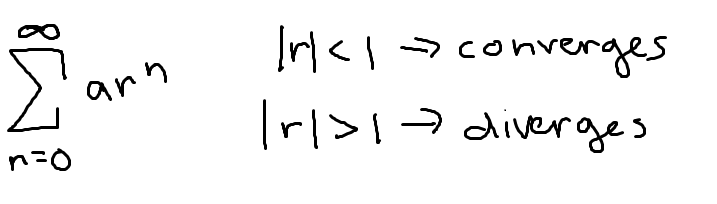
p-series test

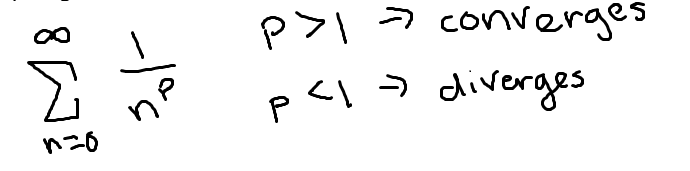
Alternating series test

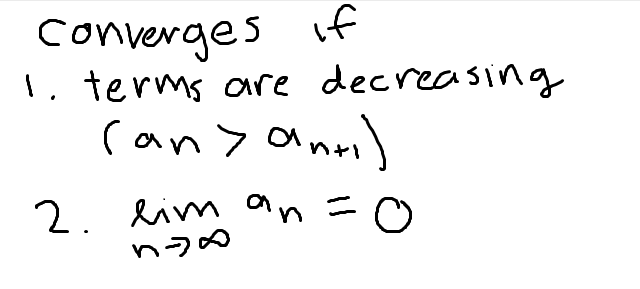
Integral test

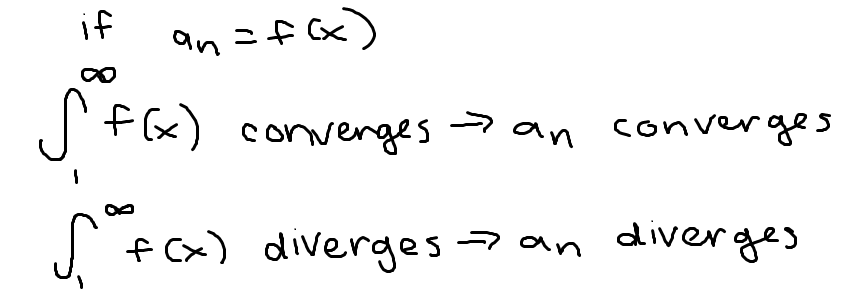
Ratio test

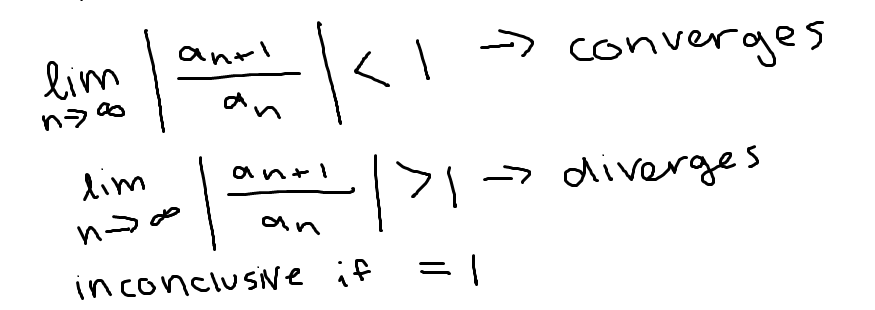
Direct comparison test

A series with smaller terms than a known convergent series will also converge

A series with larger terms than a known divergent series will also diverge

Limit comparison test

usually compared to a p-series

conditions for a function’s continuity at a point

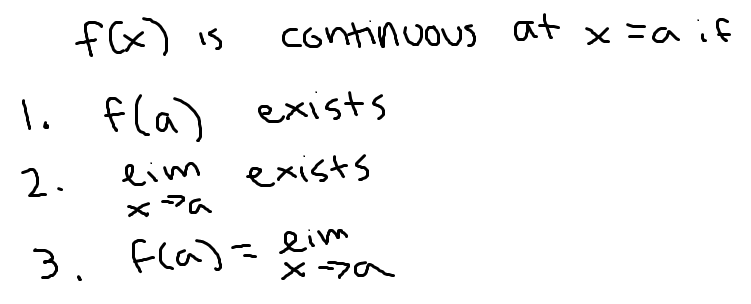
power series for 1/(1-x)

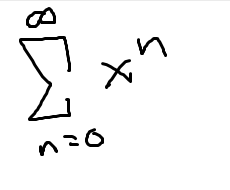
Washer method (revolved volume of an areas between two curves)

where R(x) is outer radius and r(x) is inner radius

dx for around the x-axis or other horizontal line

dy for around the y-axis or other vertical line

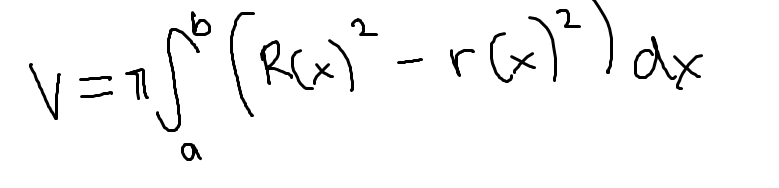
Squeeze theorem

Extreme value theorem

If f(x) is continuous on [a,b] then it must have an absolute maximum value and an absolute minimum value on that interval

Trapezoidal Riemann Sum

Overestimate when concave up

Underestimate when concave down

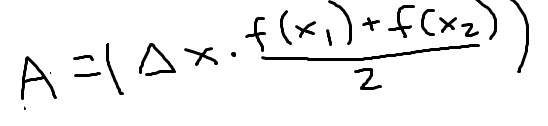
Sum of a geometric series

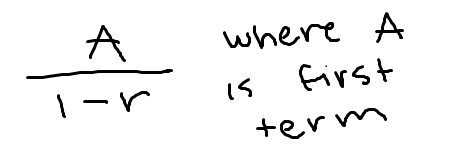
Relationship between f and its first two derivatives (for derivative tests)

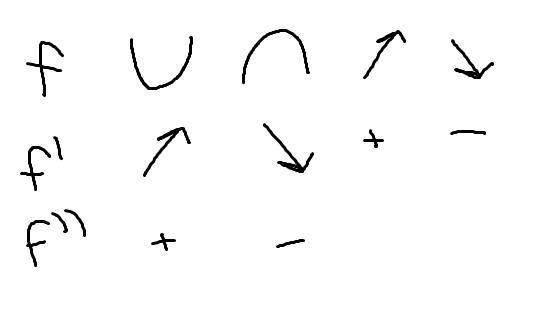
Displacement

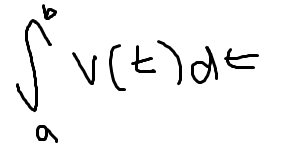
Total distance

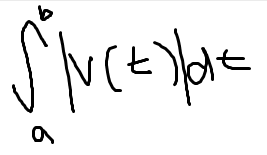
Current position

where s(a) is initial position

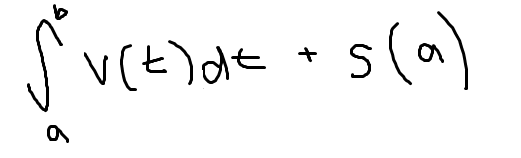
Speed

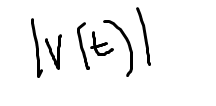
Volume with cross-sections

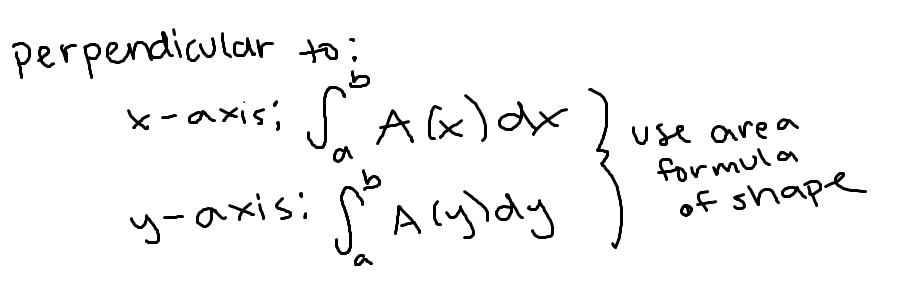
Special limit property for sine

note that x may be a quantity (such as 4x) as long as it’s the same in the numerator and denominator

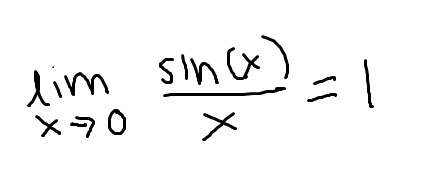
Special limit property for cosine