Prob Stats: Ch 5: Discrete Random Variables

What is a Random Variable (RV)?

A function (X) from a sample space that outputs information about the result of some random eperiment

It’s called a Random Veraible because we dont decide what to “put in” the function X

Define Range

the set of all possible values that are the result of the function X.

Discrete

When the range of X is countable (usually a subset of integers).

ex: Age of a random student

Continuous

When the range of X contains an interval

ex: amount of time spent waiting at a cross walk

Probability Mass Function (pmf)

Describes the distribution of X.

• Denoted by f(x)

• Can be graphed as a probability histogram

• The sum of all values of a pmf is 1

Cumulative Distribution Function (cdf)

F(x) = P(X ≤ x)

• Denoted by F(x)

• A non-decreasing function

• Sums the probabilities of a pmf up to a specified value

The cdf (can/cannot) be calculated from the pmf

can

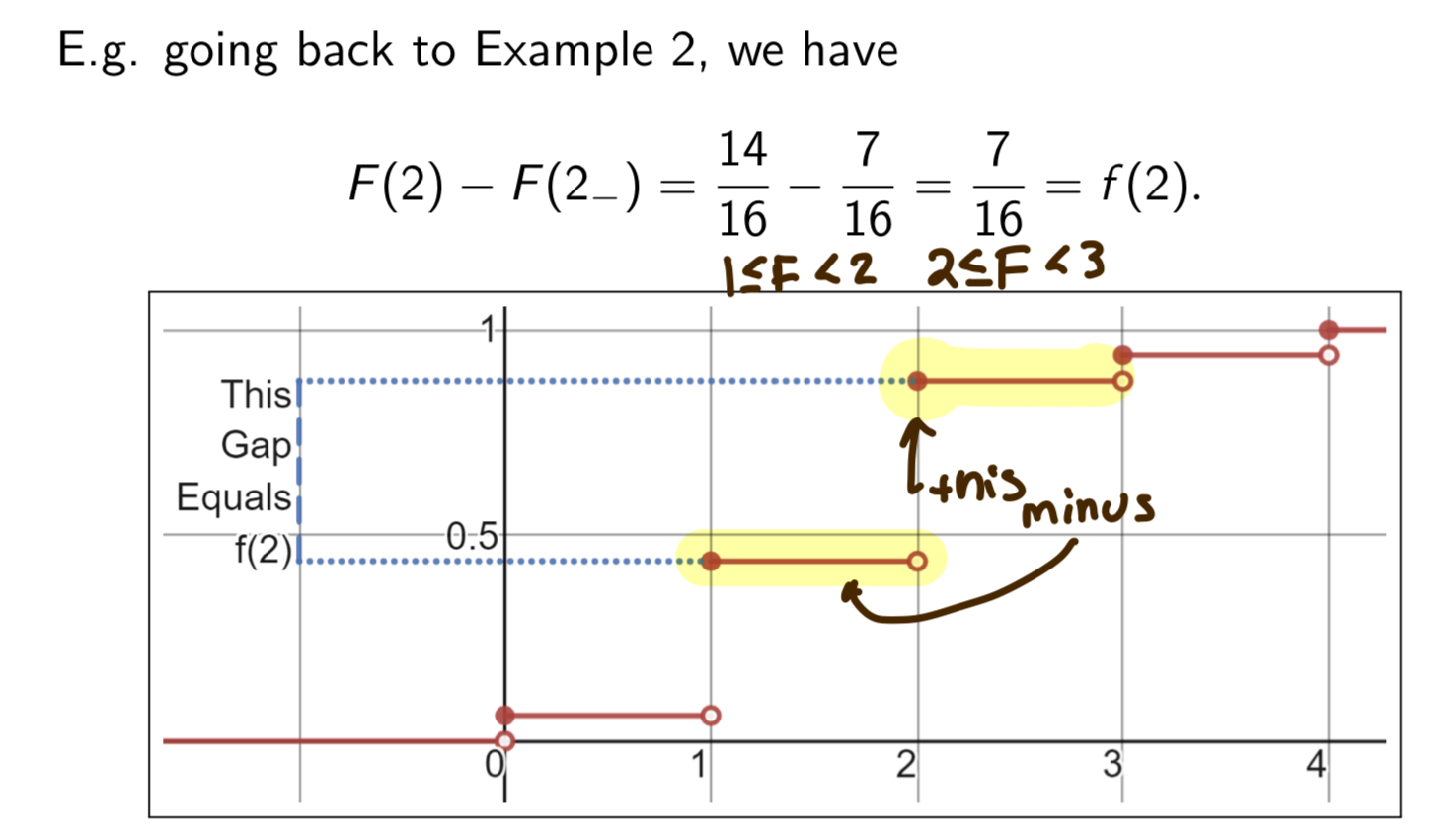
Equation for calculating pmf from cdf

f (x) = F(x) − F(x_)

Subtract the largest number in the range of X which is less than x.

Expectation Meaning & Equation

The mean of X for a discrete random variable with pmf f(x).
E(X)=μX =SUM of All xf(x)

Variance Equation

Measures the variability of X. V(X) is always ≥ 0.P

V(X)=σ² subscript x = SUM of All (x−μX)²f(x)

or

V(x)= SUM of All (x-E)²f(x)

or

V(X)= E(X²)-[E(X)]²

Standard Deviation for any RV X

σ subscript x = sqrt σ² subscript x

or

σ subscript x = sqrt V

Properties of Expectation and Variance

Independent RVs

Two random variables X1 and X2 are independent if the value taken by one of them does not influence the value of the other.

P(X1 =j and X2 =k)=P(X1 =j)P(X2 =k)

Variance for Independent RVs

If X1 and X2 are independent RVs,

V (X1 + X2) = V (X1) + V (X2)

and

V (X1 − X2) = V (X1) + V (X2)

What is a Bernoulli Distribution

Represents the probability of a single "yes/no" outcome in an experiment (1 Trial). Can be described by one parameter (p: the success probability).

Mean: p

Variance: pq

X~ Bernoulli (p)

What is a Binomial Distribution?

A Bernoulli distribution with n repeated trials that counts the number of trials are successes and failures.

X~ Binomial (n,p)

n= # of trials

p= success probability for each trial

Failure probability (q)= 1-p

Probability Mass Function (pmf) of Binomial Distribution

p= success probability for each trial

Failure probability (q)= 1-p

Expectation for a Binomial Distribution

The expected number of successes in an experiment. aka the mean
E(x)= np

Variance of a Binomial Distribution

V(x) = npq

Hypergeometric Distribution

An experiment involving drawing without replacement. (trials are NOT independent).

X~ Hyp.Geo. (N, K, n)

N= population size

K= # of sucesse states in population

n= # of draws

k= number of observed successes

Mean & Variance of Hypergeometric Distribution

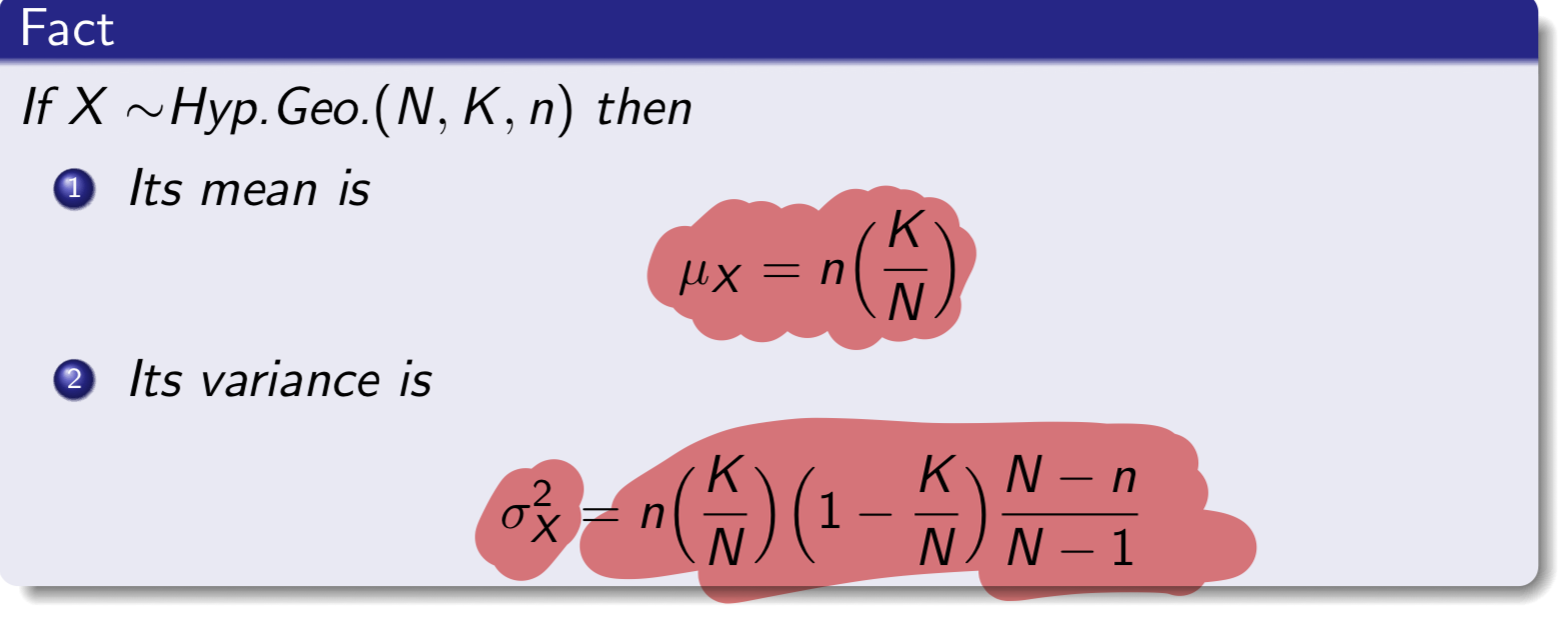
In what case can a Hypergeometric Distribution estimate a binomial distribution?

IAs population size and # of success states in the population approach infinity. Also when K/N approaches p (probability of success states)

Poisson Distribution

discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space, if these events occur with a known constant mean rate (λ) and independently of the time since the last event.

X~ Poisson (λ)

→ pmf equation in image

k= number of success states

ex: # of Amoeba offspring produced at a set interval of time.

In what case can a Poisson Distribution estimate a binomial distribution?

As n (number of trials) approaches infinity and when np(the mean of binomial distribution) approaches the rate λ.

Expectation and Variance of Poisson distribution