Experiment 2 - Part 3

1. How would you interpret the change in calibration polynomials as Mach number increases (M = 0.10 → 0.30)?

• As Mach number increases, both the magnitude and nonlinearity of ΔP_pitch and ΔP_yaw distributions increase.

• This is visible in the curve steepness and larger coefficients in the higher-order terms of the polynomial fits.

• The pressure gradients are stronger at higher Mach due to increased dynamic effects and angle sensitivity, justifying the 5th-degree fit.

2. Table 3.3 shows large discrepancies between ṁ_ref and ṁ from the probe at Mach 0.10. Why might this occur?

• At low Mach numbers, pressure differences are small, so sensor resolution and noise can dominate the signal.

• Minor misalignments or turbulent fluctuations have a proportionally greater impact.

• Five-hole probes are less sensitive at low dynamic pressures, reducing accuracy compared to orifice-based measurements.

3. In Table 3.1 and 3.2, why is there a large jump in q̇ at M = 0.20 compared to M = 0.10?

• q=12ρu2q = \frac{1}{2} \rho u^2q=21​ρu2, so a doubling of velocity leads to a fourfold increase in dynamic pressure.

• Also, ΔP (orifice pressure drop) increases significantly from 118 Pa to 435 Pa, indicating higher flow energy.

• The increase in kinetic energy is nonlinear with Mach → consistent with the observed jump.

4. Which method shows the most consistent results across all three Mach numbers: orifice, Pitot, or 5-hole probe?

• Based on Table 3.3, orifice meter (reference) gives consistent values.

• The 5-hole probe shows larger variation, especially at low Mach.

• Pitot data (q̇ and Re_int) aligns reasonably well with orifice but shows underestimation at higher Mach.

5. What does the comparison of m˙ref\dot{m}_{\text{ref}}m˙ref​ vs. m˙\dot{m}m˙ and QrefQ_{\text{ref}}Qref​ vs. QQQ in Table 3.3 suggest about integration quality in Measurement C?

• There’s an underestimation of mass flow in Measurement C at all Mach numbers, especially at low Mach.

• Indicates that:

  • The grid resolution may not be capturing the full velocity field.

  • The ring method may not be sufficient in capturing jet spread.

  • The probe's angle or calibration may have small systematic errors.

6. How would you estimate the uncertainty in the 5-hole probe measurement based on this data?

• Compare deviations between m˙ref\dot{m}_{\text{ref}}m˙ref​ and m˙\dot{m}m˙ from the probe.

• Use relative error:

• Include:

  • Repeatability uncertainty (same setup, different day)

  • Calibration uncertainty (fitting error from polynomial)

  • Sensor noise/error (resolution limits of pressure scanner)

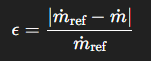
7. Why might Reynolds numbers in Table 3.3 (Reint vs Reint_ref) differ significantly even if densities are close?

• Re is directly proportional to velocity, which is derived from dynamic pressure.

• Even small errors in ΔP can cause significant velocity deviation.

• Also, local flow angles (affecting axial component) may differ in the 5-hole measurement, causing lower effective velocities and thus Re.

8. How confident are you in the polynomial fits shown in Figures 3.1 to 3.9? What’s a good way to validate them?

• Fits appear visually accurate, especially near the central range (|α|, |β| ≤ 20°).

• Confidence decreases at the edges (e.g., ±30°), where extrapolation occurs.

• Validation methods:

  • Use R² value or residual error plots.

  • Compare predicted flow angles from calibration with known reference test cases.

  • Apply the polynomial to a different dataset and evaluate performan

Q1: How do you assess the quality of your 5th-order polynomial fits?

• By visually comparing the polynomial curve with raw data (see Figures 3.1–3.9).

• The fit follows the data trends smoothly, especially near α, β = 0°, which is most critical.

• Residual scatter appears moderate, indicating acceptable fit.

• Could improve by calculating R² values or standard error (not shown in report but would strengthen it).

Q2: What is the influence of increasing Mach number on ΔP vs. angle behavior?

• As Mach number increases (0.1 → 0.3), the magnitude of pressure differentials (ΔP) increases significantly.

• Curves become steeper and more nonlinear, especially for pitch.

• This shows the probe’s sensitivity increases with flow speed, but also demands more accurate fitting at higher Mach numbers to avoid saturation or nonlinearity errors.

Q3: Why are the values from the 5-hole probe and orifice meter different (see Table 3.3)?

• Differences arise due to:

  • Measurement method nature: intrusive (5HP) vs non-intrusive (orifice).

  • Assumptions: axisymmetry, laminar vs. turbulent flow.

  • Integration grid resolution in 5HP.

  • Empirical coefficients (Cd, ε) in ISO 5167-2.

• Measurement noise and temporal mismatch can also contribute.

Q4: What trend do you observe in flow rate (ṁ and Q) across Mach numbers?

• From Ma = 0.1 to 0.3, orifice meter reports increasing ṁ (0.07 → 0.2 kg/s).

• 5HP estimates are significantly lower at low Mach (e.g. 0.01 kg/s at Ma=0.1).

• This suggests either underestimation by 5HP (due to grid spacing or calibration error) or overestimation by orifice (less likely if Cd, ε are correctly applied).

Q5: Table 3.3 shows qref and q differ. What could explain the discrepancy in dynamic pressures?

• Dynamic pressure q = ½ ρu² is sensitive to:

  • Velocity estimation accuracy (from angle & ΔP via polynomial).

  • Local density assumptions — barometric pressure/sensor lag.

• Discrepancies suggest flow field is not perfectly uniform, or there’s an alignment/mapping error in some parts of the probe.

Q6: If you had to trust only one method to report mass flow, which would you pick and why?

Likely the orifice meter due to:

• Standardized method (ISO 5167-2) with known uncertainty margins.

• Less sensitive to probe alignment or grid resolution.

• However, it’s non-local and less suitable for spatial diagnostics.

Q7: What uncertainty sources are systematic and which are random across your three methods?

Systematic:

• Calibration error in 5HP polynomial.

• Misalignment in probe positioning.

• Incorrect β or Cd in orifice calculations.

Random:

• Ambient pressure/temperature fluctuations.

• Electrical noise in pressure scanners.

• Local turbulence during measurement.

Q8: Suggest one improvement for each method (5HP, Orifice, Pitot).

• 5HP: Use denser measurement grid, particularly near jet core.

• Orifice: Validate Cd using actual test rig geometry, not just standard tables.

• Pitot: Use multi-point traverse or rake to better capture representative flow.