Displaying & Summarizing Quantitative Data

Quantitative Data

numerical data that represents a specific quantity, amount, or range of numbers

Ways to represent quantitative data

• Histograms

• Steam & Leaf Displays

• Dotplots

• Boxplots

How to make a histogram

1. Decide on an appropriate bin width

2. Create a frequency table to organize the data into appropriate bins

3. Label axes appropriately, if there needs to be a break in the graph…put it. The x-axis will contain the bin values and the y-axis is the frequency

4. Construct the histogram by creating vertical bars whose height represent the quantity of values in the specified bin

5. Make sure there are NO gaps between the bars (unless the bin is empty) and there’s appropriate titles and equal bin widths

Stem and Leaf Displays

Organized into bins (stems) and allows one to see the individual data point and modes. Needs a key and could usually only be used for 2-3 digits whole numbers

Truncating the values

usually happens when the numbers are too large and need to round them to put them in the display

Dotplots

most simple display and used to visualize simulations. Works best with a small range of numbers

“Quantitative Data” condition

A condition that verifies that the data is numerical and the units are known

Questions about SHAPE to ask oneself

1. Does this histogram/stem&leaf plot/dotplot have a single central hump of data, or several separated humps?

2. Is the histogram symmetric?

3. Do any unusual features stick out?

4 Main types of Shape (Distribution)

1. Symmetric

2. Uniform

3. Skewed left

4. Skewed Right

Symmetric

Same on both sides if folded at the highest bar

Uniform

When the data is almost the same

Skewed left

Little bit of data on the left and the central part of the data on the right (mean <median)

Skewed Right

Tail on the right and the rest of the data on the left (mean>median)

Roughly symmetrical

Occurs because real-life data is never perfect

Bimodal

Kinda symmetrical but has 2 modes (can be asymmetrical)

Make sure to mention ___ while describing shape

OUTLIERS (either be the most informative part of data or an error)

Median

Middle of the data points

Ways to describe the spread

Range, IQR, Standard Deviation

Range

max. - min.

Interquartile Range (IQR)

Difference between the upper and lower quartiles

Five Number Summary

reports the min., 1st quartile, median, 3rd quartile, and max. of a set of data. This breaks the data up into 4 sections that gives 25% of the data in each section

Outliers

When the data is not within the bounds of the fences/ if it’s more than 1.5 times the distance of the middle 50% (usually the min. and max.)

Lower Fence

Q1 - 1.5(IQR)

Upper Fence

Q3 + 1.5(IQR)

Describing data for when its symmetric

Use the mean and standard deviation

Mean formula

Add up all the data points then divide the sum by the number of data points

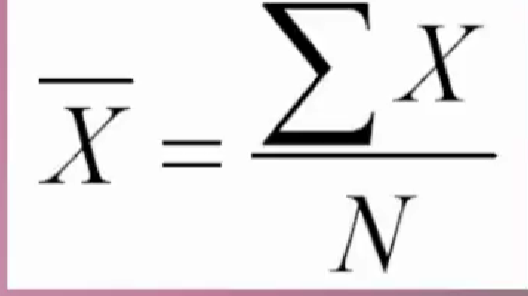
Standard Deviation Formula

Take the mean and subtract every single data point from the mean, then square it (for every single data point in the set) add them all together, then divide by either N (Population) or n-1 (sample)

When the shape is skewed (Data Description)

Use the median and IQR because they are not affected by outliers (since they are positional values)

What to Tell About a Quantitative Variable

1. Start by making one of the pictures and discuss the shape of the distribution

2. Next, discuss the center and spread. Always pair the median with the IQR and the mean with SD. NEVER REPORT A CENTER WITHOUT A SPREAD

3. If the shape is symmetric use the mean and SD. If it’s skewed, use the median and IQR (Might want to report mean and SD too but note WHY it’s different)

4. Discuss any unusual features. If there are multiple nodes, discuss that and try to explain why if possible. If there are clear outliers, try and report the data with and without them to show their influence.

What can go wrong?

• Dont make a histogram of categorical data

• Dont look for shape, center, and spread of a bar chart

• Dont use bars for every display.. save them for histograms and bar charts

• Choose an appropriate bar width

• Dont round in the middle of a calculation

• Watch out for multiple modes

• Beware of Outliers

• Dont forget to sort out the data before finding medians and percentiles

• Dont report too many decimal places