StemUp: OCR A A level Physics 3.1: Motion

What is meant by speed? (1)

The rate of change of distance; it is a scalar quantity.

What is the difference between average speed and instantaneous speed? (2)

- Average speed is the total distance travelled divided by total time taken.

- Instantaneous speed is the speed of an object at a specific moment in the journey and cannot be calculated using v = Δx/Δt.

What is meant by velocity? (1)

The rate of change of displacement; it is a vector quantity.

What is the difference between average velocity and instantaneous velocity? (2)

- Average velocity is the total displacement divided by total time taken.

- Instantaneous velocity is the velocity at a specific moment in the journey and cannot be calculated using v = Δs/Δt.

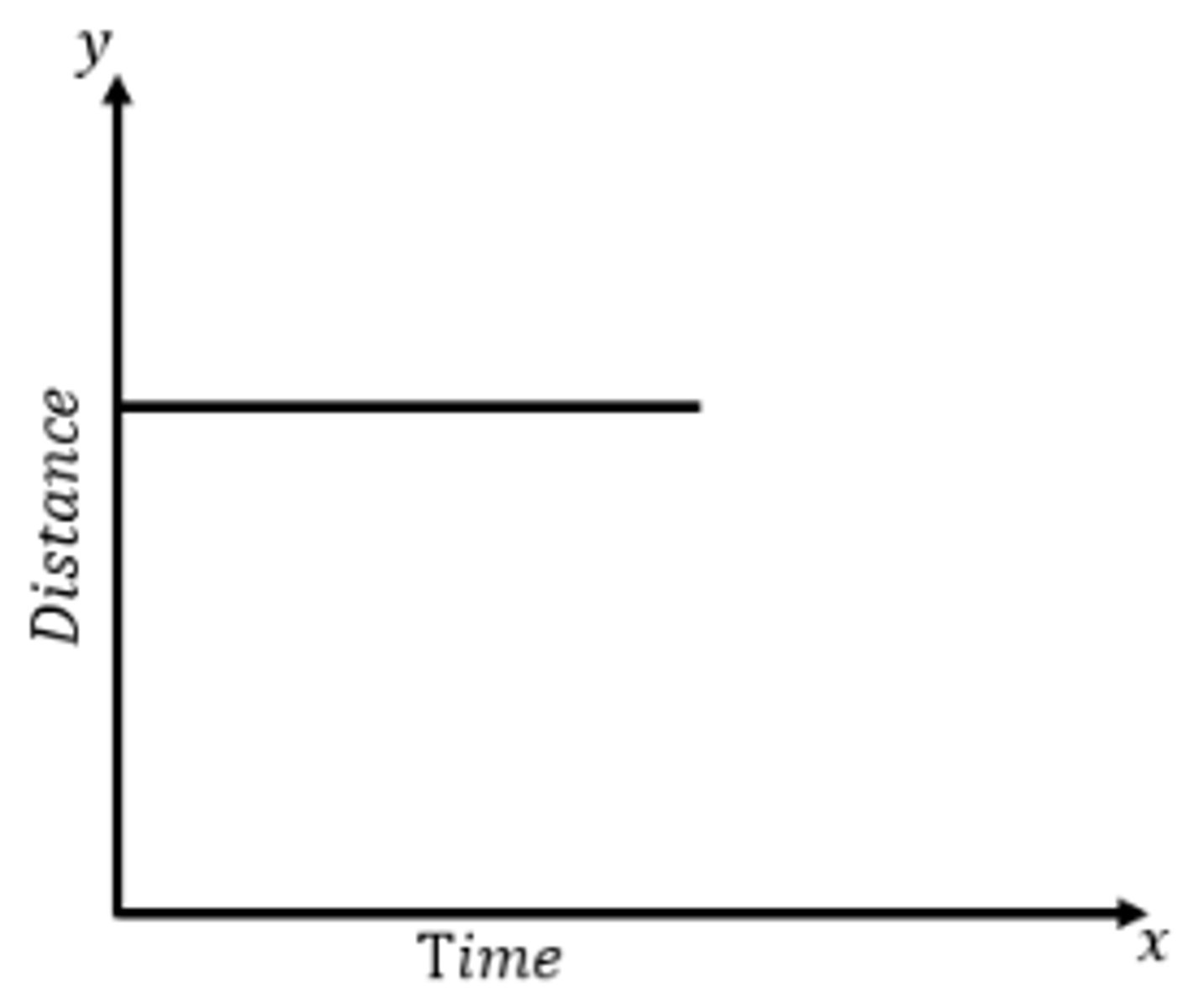
Draw a distance-time graph for a stationary object. (1)

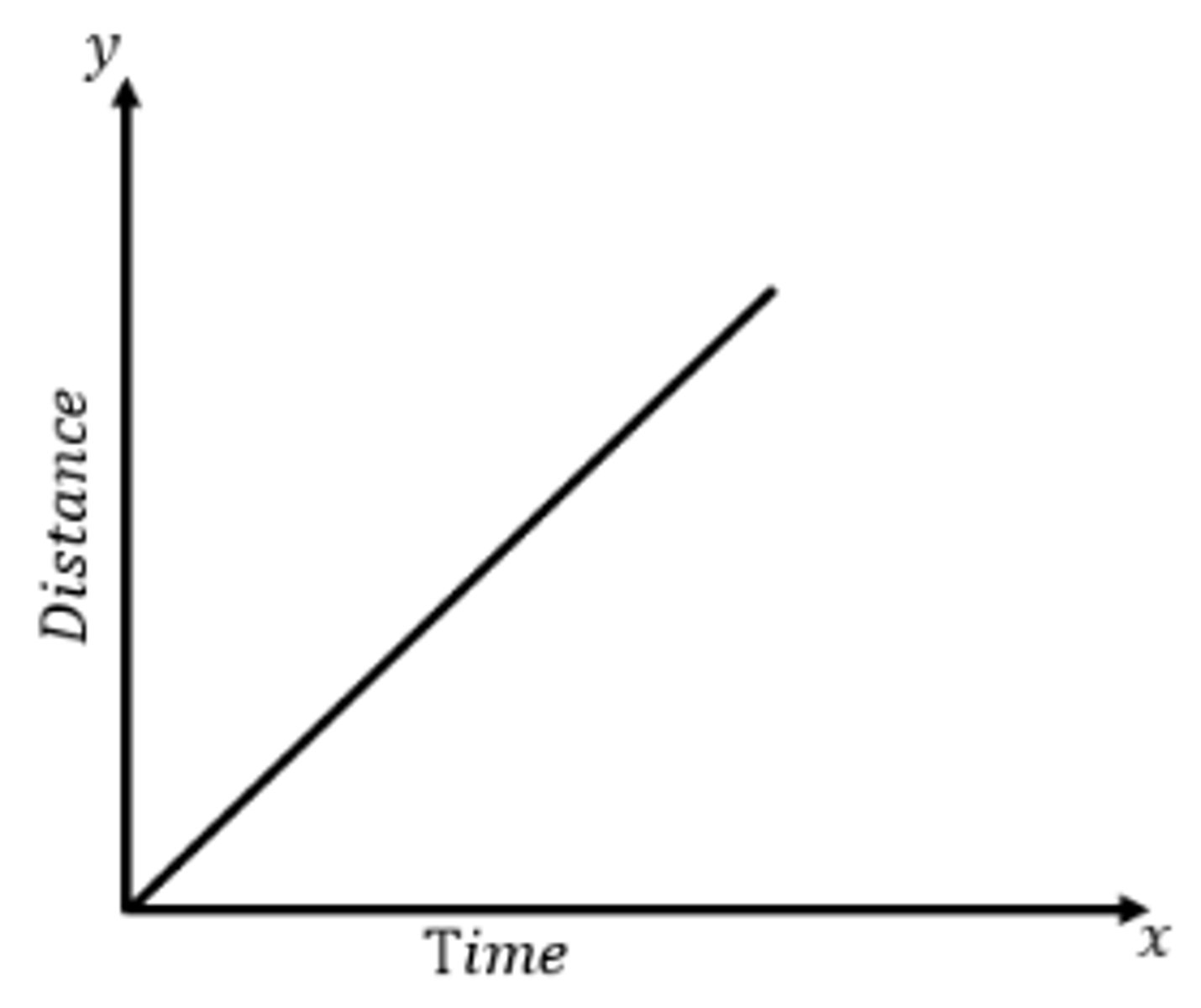
Draw a distance-time graph for an object moving at constant speed. (1)

What would the displacement-time graph look like for an object moving with constant speed in one direction, then the same speed in the opposite direction? (2)

- A straight line with constant positive gradient ...

- Which is then followed by a straight line with equal negative gradient.

How can you calculate average and instantaneous speed/velocity from a graph? (2)

- Average: Find the overall gradient of the distance-time or displacement-time graph.

- Instantaneous: Draw a tangent at the desired time and calculate its gradient.

Why are average speed and average velocity often different? (3)

- Speed depends on total distance (which is always positive), while velocity depends on displacement (which can be negative).

- An object returning to its starting point has zero average velocity but non-zero average speed.

- They are only equal when the object travels in a straight line without changing direction.

What does maximum speed looks like on a displacement-time graph? (1)

Maximum speed is the steepest section of the graph.

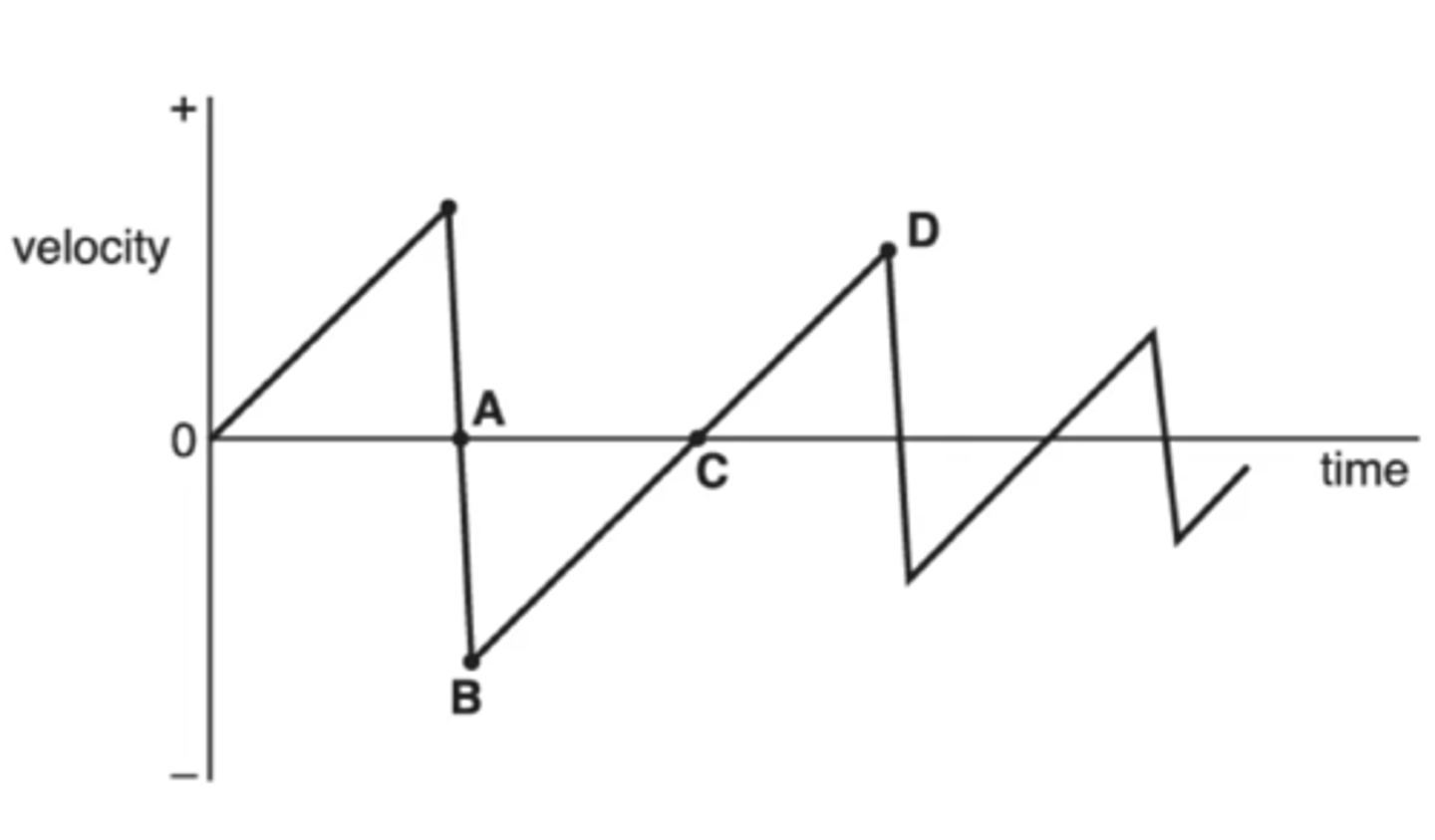
Draw a velocity-time graph of a bouncy ball dropped from a height h. (2)

What is meant by acceleration and what are its units? (2)

- Acceleration is the rate of change of velocity.

- It is a vector quantity with units m/s^2.

What are two methods for determining acceleration? (2)

- Use a = Δv/Δt.

- Use the gradient of a velocity-time graph.

What do velocity-time graphs look like for stationary objects vs objects moving at constant velocity? (2)

- Stationary objects are represented by a horizontal line at v = 0.

- Objects with constant velocity are represented by a horizontal line above (or below) the time axis.

What do velocity-time graphs look like for uniform vs non-uniform acceleration? (2)

- Uniform acceleration is represented by a straight line with constant gradient.

- Non-uniform acceleration is represented by a curved line with varying gradient.

Why might the velocity-time graph not be a straight line for an object moving with constant speed? (2)

- Speed may be constant but direction can change (e.g. circular motion).

- Since velocity includes direction, the graph must account for this.

How does a velocity-time graph differ for constant acceleration vs constant deceleration? (2)

- Constant acceleration is represented by a straight line with positive gradient.

- Constant deceleration is represented by a straight line with negative gradient.

How would you calculate average and instantaneous acceleration using a velocity-time graph? (2)

- Average velocity is the gradient between two points.

- Instantaneous velocity is the gradient of a tangent at a specific point in the journey.

How would you find displacement using a velocity-time graph when acceleration is constant? (1)

The displacement is the area under the graph which can be found by using the trapezium rule.

How would you find displacement using a velocity-time graph when acceleration is not constant? (1)

Estimate area under the curve e.g. by counting squares.

What are the five physical quantities used in the suvat equations? (5)

- Displacement (s)

- Initial velocity (u)

- Final velocity (v)

- Acceleration (a)

- Time (t)

What are the four suvat equations used for motion with constant acceleration? (4)

1. v = u + at.

2. s = 1/2 (u + v)t

3. s = ut + 1/2 at^2

4. v^2 = u^2 + 2as

How is the equation v=u+at derived from a velocity-time graph? (2)

- The gradient of a velocity-time graph represents acceleration, so a=(v-u)/t, which is the change in velocity divided by the time taken.

- This rearranges to v=u+at.

How is the equation s=1/2(u+v)t derived from a velocity-time graph? (2)

- The displacement of an object is represented by the area under the velocity-time graph.

- Using the trapezium rule to calculate this area gives s=1/2(u+v)t.

What is meant by free fall? (1)

The motion of an object under the influence of gravity alone, with no other forces acting on it.

What does the symbol g represent in the context of free fall? (1)

It represents the acceleration due to gravity, which is approximately 9.81 m/s^2 near the surface of the Earth.

What is meant by thinking distance? (1)

The distance a vehicle travels from the moment the driver sees a hazard to the moment they apply the brakes.

What is meant by braking distance? (1)

The distance a vehicle travels from when the brakes are applied until it comes to a complete stop.

What is meant by stopping distance? (1)

The total distance a vehicle travels from first seeing a hazard to coming to a complete stop: the sum of the thinking and braking distances.

What factors affect a driver's thinking distance? (4)

- Tiredness

- Alcohol or drugs (intoxication)

- A longer reaction time

- Vehicle speed

What factors affect braking distance? (3)

- The mass of the vehicle

- The condition and quality of the brakes

- The condition of the road surface (e.g. wet or icy)

Why are the horizontal and vertical components of a projectile's velocity independent of one another? (3)

- The force of gravity acts only in the vertical direction, causing acceleration in that direction.

- The vertical component of the velocity is therefore affected by gravity and changes throughout the motion.

- The horizontal component is unaffected by gravity and remains constant (assuming no air resistance).

How would you calculate the maximum height of an object thrown vertically upwards? (2)

- Use the suvat equation v^2 = u^2 + 2as, where the final vertical velocity v = 0 at the maximum height.

- Rearranging the equation gives the displacement s, which is the maximum height reached.

Why does the resultant force on a projectile experiencing air resistance not act directly opposite to its velocity? (2)

- Air resistance acts in the opposite direction to the velocity vector.

- However, the projectile is also affected by weight acting vertically downwards, so the resultant force is the vector sum of air resistance and weight which is not directly opposite the velocity.

How does the kinetic energy of a projectile change as it rises to its maximum height? (2)

- The kinetic energy decreases as the projectile gains height.

- At the maximum height, the kinetic energy is at its minimum.

How would you find the total time of flight of an object thrown at an angle to the horizontal on flat ground? (2)

- Use the suvat equation v = u + at in the vertical direction with v = 0 to calculate the time to reach the maximum height.

- Double this value to find the total time of flight (as the ascent and descent times are equal).

How would you calculate the horizontal range of a projectile launched at an angle? (3)

- First calculate the time of flight using vertical motion and the suvat equation v = u + at, setting v = 0 at maximum height.

- Double this value to get the total time of flight.

- Multiply the horizontal component of the initial velocity by the total time of flight to find the horizontal range.

How would you find the velocity of a projectile at any point in its motion? (4)

- Resolve the initial velocity into horizontal and vertical components.

- Use v = u + at to calculate the vertical velocity at the required time.

- Use Pythagoras' theorem to combine the horizontal and vertical components to find the magnitude of the velocity.

- Use trigonometry to calculate the direction of the velocity vector relative to the horizontal.