ap precalc test prep

rate of change formula

y₂-y₁/x₂-x₁

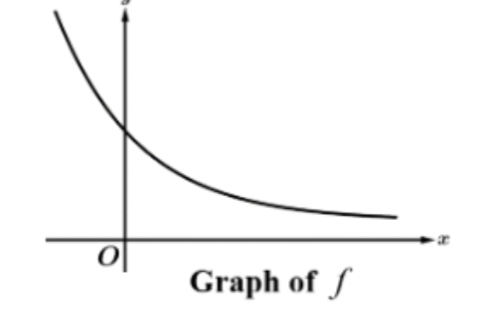
positive or negative, increasing or decreasing

positive and decreasing

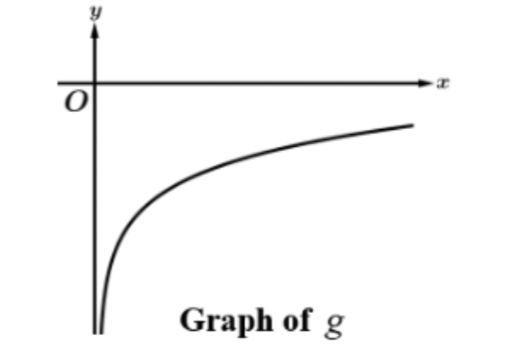
positive or negative, increasing or decreasing

negative and increasing

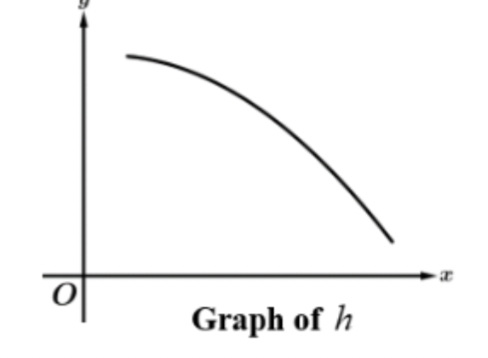
positive or negative, increasing or decreasing

positive and decreasing

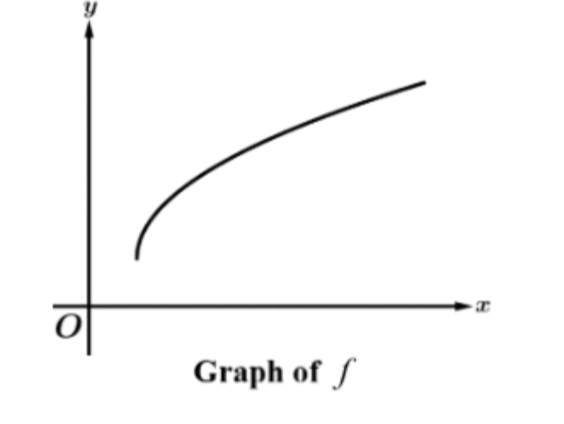
positive or negative, increasing or decreasing

positive and decreasing

what is multiplicity?

the degree of the factor

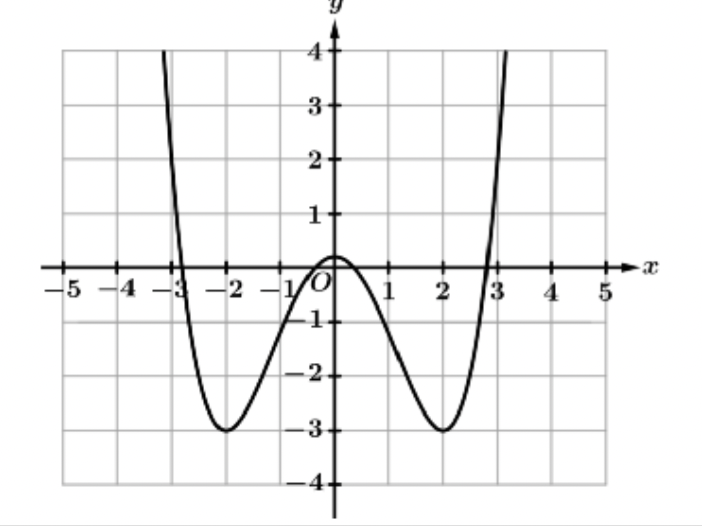
even functions

an even function is symmetric over the y axis

f(-x)=f(x)

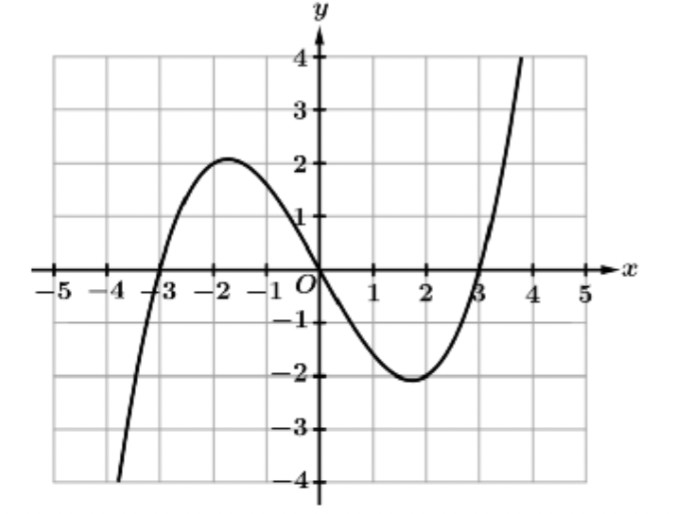
odd function

an odd function is symmetric about the origin

g(-x)=-g(x)

what translation/dilation is f(x)+k

vertical dilation of k units

what translation/dilation is f(x+k)

horizontal translation of -h units

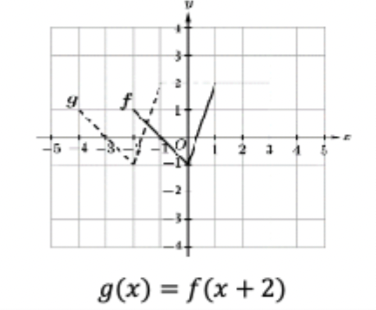
what translation/dilation af(x)

f has a vertical dilation by a factor of |a|, if a<0, f is reflected over the x-axis

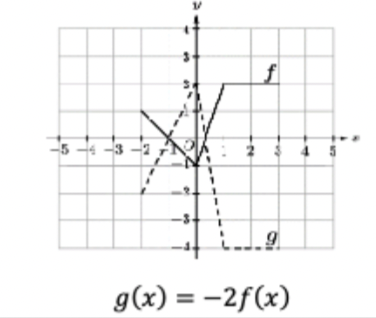
what translation/dilation is f(bx)

f has a horizontal dilation by a factor of |1/b|. if b<0, f is reflected over the y-axis

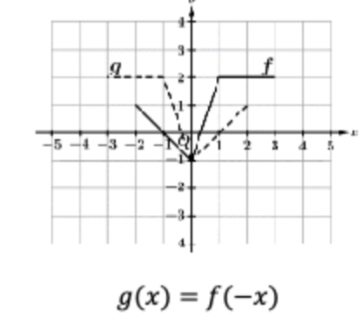
vertical asymptote

when function is undefined, set the denominator=0 and let each factor in the denominator=0

holes

when you cancel a factor in the numerator and denominator. set the cancelled factor to 0

horizontal asymptote

if the power of the numerator is ___ than the denominator

n<d, HA y=0

n>d, no HA

n=d, HA = leading coefficient on the numerator/leading coefficient on the denominator

slant asymptote

when n>d, there is a slant asymptote. divide numerator by denominator

arithmetic sequence

common difference

behave like linear functions, except they’re not continuous.

increasing arithmetic sequences increase equally each step (slope stays the same)

geometric sequence

common ratio/constant proportional change

behave like exponential functions, except they’re not continous

increaisng geometric sequences increase by a larger amount each step (% increase always stays the same)

exponential functions

a(b)^x, b>0

a represents the initial amount

b represents the base of common ratio

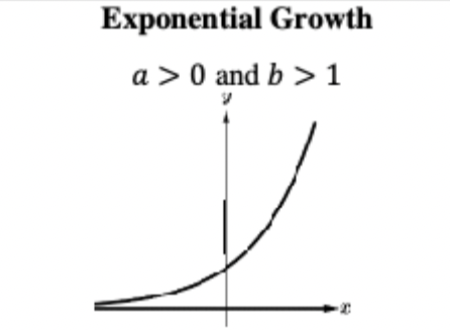
exponential growth, a and b values

a>0, b>1

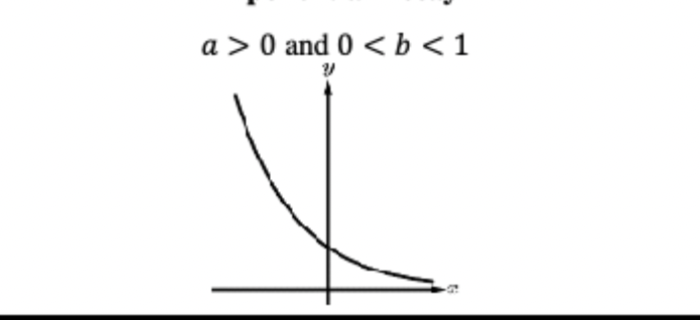
exponential decay, a and b values

a>0, 0<b<1

product property exponent rule

power property exponent rule

negative exponent property rule

how to calculate residentuals

residual=observed value-predicted value

this is also referred to as the error in the model

how to know if the residual model is appropriate

they will have points randomly scattered above and belove the x axi. think of the sum of the residuals being 0

2 ways composite functions can be written

(f o g)(x) or f(g(x))

inverse functions

these can be found by switching x and y.

exponential and logarithmic form of log functions

log function characteristics

always concave up or concave down

always increasing or decreasing

vertically asymptotic to x=0

domain is typically (0,infinity)

range is typically (-infinity, infinity)

product property

quotient property

power property

change of base property

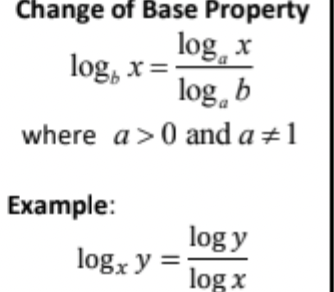
period

a period is the length of the x values that it takes for the function to complete 1 cycle

standard position

in the coordinate plane, an angle is in the standard position when its vertex is at the origin and one ray of the angle lies on the positive x-axis

terminal ray

the terminal ray is the second ray of an angle in standard position

positive angles

counterclockwise direction

negative angles

clockwise direction

reference angle

the distance between the terminal ray and nearest x-axis (must be a positive acute angle)

sin displacement

sin is the ratio of vertical displacement

sin⍬ = y/r

cos displacement

cos is the ratio of horizontal displacement

cos⍬ = x/r

tan displacement

tan is the slope of the terminal ray

the ratio of the vertical displacement to the horizontal displacement

tan⍬ = y/x

tan⍬ = sin⍬/cos⍬

coordinates of a point on a circle centered at the origin

cos⍬ = x/r

sin⍬ = y/r

unit circle quadrant one (1) values

0 = (1,0

π/6 = √3/2, 1/2

π/4 = √2/2, √2/2

π/3 = 1/2, √3/2

π/2 = 0,1

unit circle quadrant two (2) values

2π/3 = -1/2, √3/2

3π/4 = -√2/2, √2/2

5π/6 = -√3/2, 1/2

π = (-1,0)

unit circle quadrant three (3) values

7π/6 = -√3/2, -1/2

5π/4 = -√2/2, -√2/2

4π/3 = -1/2, -√3/2

3π/2 = 0, -1

unit circle quadrant four (4) values

5π/3 = 1/2, -√3/2

7π/4 = √2/2, -√2/2

11π/6 = √3/2, 1/2

2π = 1,0

properties of f(⍬) = sin⍬

average period with no shifts: 2π

frequency is the reciprocal of the period, 1/2π

the graph of f(⍬) = sin⍬ oscillates between concave down and concave up

properties of g(⍬) = cos⍬

period with no shifts: 2π

frequency is the reciprocal of the period, 1/2π

the graph of g(⍬) = cos⍬ oscillates between concave down and concave up

sinusoidal functions

a sinusoidal function is any function that involves additive and multiplicative transformations of f(⍬) = sin⍬

the sin and cosin functions are both sinusoidal functions because g(⍬) = cos⍬ = sin(⍬+π/2)

transformations of a sin function

the midline is a vertical translation

the amplitude is a vertical dilation

the period is the result of a horizontal dilation

phase shift of a sinusoidal function

a horizontal translation of a sinusoidal function is called the phase shift

the graph of g(x) = sin(x+c) is a phase shift of the graph of f(x) = sin(x) by -c units

the same result can be applied to the cos function

properties of the tan function

domain is all real x values, x ≠ π/2 +nπ (n E Z)

range is -infinity, infinity

period: π

vertical asymptotes: x ≠ π/2 +nπ (n E Z)

tangent equation

y=atanb(x-c)+d

a reprsents the vertical stretch/compression and indicates positive or negative to find the relative max/min

b is the frequency and helps you find the period, π/b

c is the phase shift

d is the vertical shift and midline

the asyptotes of a tangent function can be found by -π/2 < b(x-c) < π/2

tangent 5 point patter: asymptote, relative min, mid, relative max, asymptote

inverse trig functions

always consider the domain restrctions

the range of inverse sin is -π/2, π/2

the range of inverse cos is [0, π]

the range of inverse tan is -π/2, π/2

general solutions to sin functions

sinx = ½

x = π/6 +2πk, where k is an interger

x = 5π/6 + 2πk, where k is an integer

general solutions to cos functions

cosx = ½

x = π/3 + 2πk, where k is an integer

x = 5π/3 + 2πk, where is an interger

general solutions to tan functions

tanx = 1

x = π/4 +πk, where k is an integer

since the period of tangent is π, one equation will capture all solutions

secant reciprocal function

secx = 1/cosx, where cosx ≠ 0

secant is the reciprocal of the cosine function

cosecant reciprocal function

cscx = 1/sinx, where sinx ≠ 0

cosecant is the reciprocal of the sin function

cotangent

cotx = 1/tanx, where tanx ≠ 0

cotx = cosx/sinx, where sinx ≠ 0

pythagorean identity and equivalent forms

sin²⍬ + cos²⍬ = 1

1 + tan²⍬ = sec²⍬

1 + cot²⍬ = csc²⍬

sum and difference identities

sin (α ± β) = sinαcosβ ± cosαsinβ

cos (α ± β) = cosαcosβ ± sinαsinβ

double angle identities

sin(2⍬) = 2sin⍬cos⍬

cos(2⍬) = cos²⍬ - sin²⍬ = 1-2sin²⍬ = 2cos²⍬-1

polar coordinates

(r, ⍬)

converting from polar to rectangular

we know that cos⍬ = x/r and sin⍬ = y/r

x=rcos⍬

y=rsin⍬

converting from rectangular to polar coordinates

(x,y) to (r,⍬)

we know that x²+y²=r²

tan⍬ = y/x to find the value of ⍬