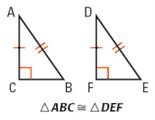
Congruent triangles
1/16
There's no tags or description
Looks like no tags are added yet.
Name | Mastery | Learn | Test | Matching | Spaced |
|---|
No study sessions yet.
17 Terms
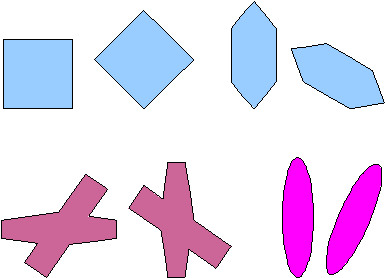
congruent figures
Figures that have the same size and shape
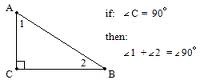
Corollary to the Triangle Sum Theorem
The acute angles of a right triangle are complementary
Corollary to a theorem
A statement that follows from already proven statement and requires little or no proof
Triangle Sum Theorem
The sum of the measures of the interior angles of a triangle is 180 degrees

Exterior Angles Theorem
The measure of an exterior angle of the triangle is equal to the sum of the measures of the two no adjacent interior angles
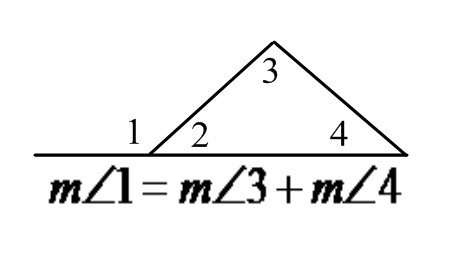
CPCTC
Congruent Parts of Congruent Triangles are Congruent
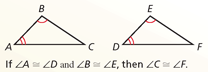
Third Angle Theorem
If two angles of one triangle are congruent to two angles of a second triangle, then the third angles of the triangle are congruent
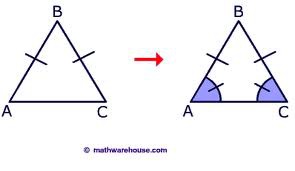
Base Angle Theorem (Isosceles Triangle)
If two sides of a triangle are congruent, the angles opposite these sides are congruent.
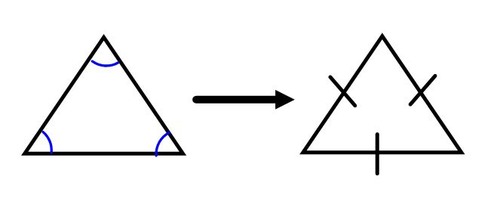
Corollary to the Converse of the Base Angles Theorem
If a triangle is equiangular, then it is equilateral
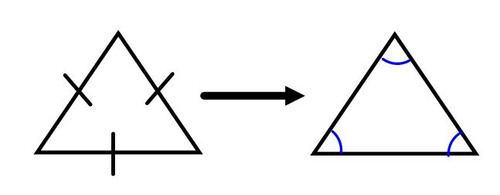
Converse of the Base Angles Theorem
If two angles of a triangle are congruent, then the sides opposite them are congruent.

Corollary to the Base Angles Theorem
If a triangle is equilateral, then it is equiangular
Congruent triangles
2 triangles are congruent if and only if all pairs of corresponding sides and angles are congruent
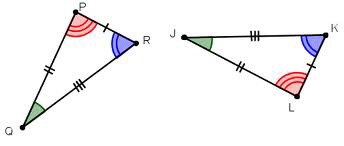
SAS
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent
SSS
If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
AAS
if two angles and a non-included side of one triangle are congruent to the corresponding two angles and side of a second triangle, then the two triangles are congruent
ASA
If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the two triangles are congruent
HL Theorem (hypotenuse-leg)
If the hypotenuse and leg of a right triangle are congruent to the hypotenuse and let of a second triangle, then the two triangles are congruent