Population Ecology Final Exam

Population

a group of organisms of the same species coexisting at the same time and place

Population Ecology

the scientific study of the dynamics, regulation, persistence and evolution of biological populations

Why study population eco?

1. populations are the basic unit of ecological organization
2. evolution occurs at the population level
3. dynamics of infectious diseases can be thought of as population dynamics

Why is population ecology important in wildlife management/conservation biology?

populations are the units of conservation and management

What are the measurable characteristics of populations (or population parameters)?

1. Abundance
2. rate of birth
3. rate of death
4. emigration/immigration
5. rate of increase
6. sex ratio
7. age or stage structure


1. spatial distribution

Steps of the scientific method.

1. collect data
2. observe the pattern
3. develop a hypothesis
4. predict
5. collect more data
6. evaluate

scientific vs non scientific hypothesis

scientific: a theory intended for experimental test

non scientific: cannot be proven correct or incorrect by an experiment

statistical vs biological hypothesis

Statistical: conjectures about the predicted for the process (Ho vs Ha)

biological: posses a tentative explanation about a process observed in the natural world

 mensurative (or comparative) vs. experimental approach

mensurative: observing/measuring a system at different locations/times in a systematic way NO MANIPULATION

experimental: study designs where you randomly apply a treatment. you are manipulating a situation

control vs treatment

control: not manipulated

treatment: manipulated experimentally

randomization vs replication

randomization: applying treatment randomly

replication: repeating trials/experiment to ensure its validity

Induction

reasoning from specific to general (first three steps)

deduction

reasoning from general to specific (last four steps of sci method)

hypothetico-deduction

induction + deduction = hypothetico-deduction = scientific method

what are population growth models?

simplified, mathematical or computer representations of population growth processes

attempt to mimic the dynamics or biological populations

why are models useful in ecology?

1. models are learning tools
2. suggest hypotheses and experiments
3. help identify key components of the system
4. models make predictions
5. data analysis and synthesis
6. models can be used for management purposes
7. disease control or containment strategies
8. frequently, we have no alternative

Define population growth variables

B: birth

D: death

E: emigration

I: immigration

b: birth rate

d: death rate

Lambda calculation

experimental: Nt = lambda^t(N0)

logistical: Nt+1 = Nt + Nt(rd) \[1-Nt/K\]

r calculation

exponential: dN/dt = rN

logistical: dN/dt = Nrmax(1-N/K)

Exponential growth assumptions

1. unlimited homogeneous environment
2. no immigration or emigration
3. constant birth and death rates
4. no age/stage structure

logistical growth assumptions

1. no immigration or emigration
2. no age/stage structure
3. no stochasticity
4. linear decline in r as N increases (linear density dependence)
5. carrying capacity, K, is constant

Demographic stochasticity

unpredictable variability in population growth due to random differences among individuals in survival and reproduction

small populations are affected more severely

environmental stochasticity

unpredictable variation in demographic characteristics

due to stochastic variation in the extrinsic environmental factors

steps to incorporate stochasticity

1. assume: r \~ normal
2. for each time t, sample r from the distribution and parameters from step 1
3. project population size from time t to
4. repeat this process from t = 1 to T
5. repeat the process hundreds of times as needed
6. plot the results
7. calculate the mean and variance of the pop size
8. calculate the probability of extinction

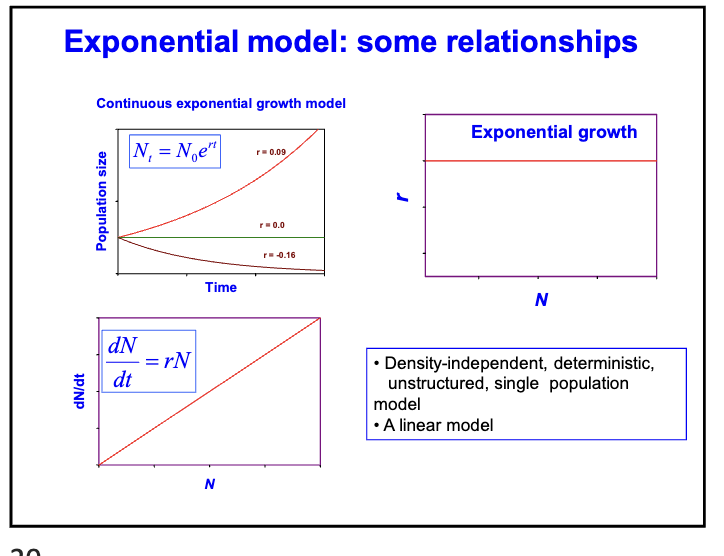
Relationship between

t and N

N and r

N and dN/dt

doubling, tripling, quadrupling time

t double = ln(2)/r

t triple = ln (3)/r

t quadruple = ln(4)/r

The exponential model makes several unrealistic assumptions. Given this, why do we need to learn about this rather unrealistic model?

This model is the stepping stone for other, more realistic, growth models

density dependence

dependence of per capita population growth rate on present or past population density

* delayed DD: dependence of r on past density
* direct DD: dependence of r on current density

important for models because it makes them more realistic

carrying capacity

the maximum number of individuals an environment can support

allee effect

positive relationship between population density and per capita population growth rate

(DD is normally a negative relationship)

Examples: mate-finding allee effect, predation dilution effect

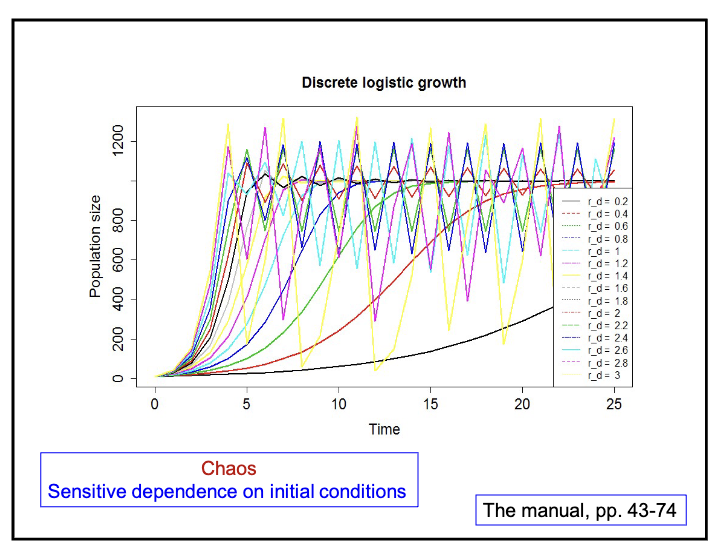
discrete-time logistic model

What is age distribution (or age structure) and why is it important in population ecology?

Age: important variable as it can influence survival and reproduction


1. birth and death rates differ among age classes
2. age structure can be used for structured demographic projections
3. age structure provides useful information regarding the past history, present or future population growth

standing age distribution

observed proportion

stable age distribution

theoretical age distribution when b and d are constant

the proportion of individuals in different age class will remain constant over time

stationary age distirubtion

SAD nad r = 0

number and proportion are constant over time

What are (ecological) life tables, and why are they useful in ecology and wildlife management? What are their assumptions?

age specific summary of survival and reproduction

they help predict future population growth rates

Assumptions:


1. no I or E
2. Unlimited, homogeneous environment
3. constant age-specific survival and fecundity rates
4. stable age distribution
5. animals of a given age are identical with respect to birth and death rates

Life table variables and their calculations

nx: # of animals of age x that are alive (cohort size)

lx: age specific survivorship (nx/n0)

dx: # of animals that die between age class x and x+1 (nx- nx+1)

qx: age specific mortality (dx/nx)

Px: age specific survival rate (1-qx)

Cohort and static life tables

Cohort life table: based on real cohorts

Static life table: based on the snap-shot of the population (not useful)

Methods of compiling life tables

1. follow real cohorts
2. mark-recapture studies
3. age at death recorded for a population with SAD, and known r
4. Age distribution is recorded at birth pulse for a population with SAD and known r

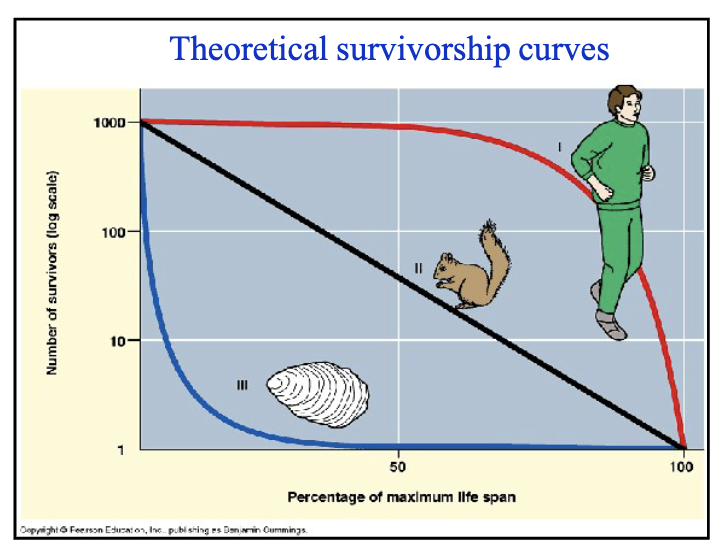
Survivorship curves

net reproductive rate (*R0*), generation time (*G*), and approximate *r* using age-specific survivorship and fecundity data (i.e., *lx* and *mx*)

R0: sum(lx\*mx)

G: sum(lx\**mx**x)/R0

r = lnR0/G

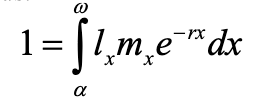
Know what the Lotka-Euler equation is, what it means, and how one can use it to calculate the exact value of *r*. Why is Lotka-Euler equation important in population ecology, wildlife management, and evolutionary biology?

Foundation of stable age theory

life history evolution and evolutionary studies rely on this theory

r is possibly the single most important quantity in ecology, evolutionary biology, and wildlife management

What are the advantages of using matrix models over life table analyses?

more organized

Assumptions of age- (and stage-) structured population models.

1. no I or E
2. unlimited, homogeneous environment
3. constant Pi and Fi
4. stable age distribution
5. non-overlapping generations
6. individuals within an age class are identical with respect to survival and reproduction

age vs age class

age: specific number

age class: range of ages in one group

pre-breeding vs post-breeding census

pre-breeding: data collected just before the birth-pulse

post-breeding: data collected just after the birth-pulse

What are the parameters of age-structured (Leslie) matrix models? How do they differ from the life-table parameters using post-breeding census method?

Parameters:

population projection matrix for AGE-STRUCTURED populations

Parameters post-breeding:


1. Pi = li/li-1
2. Fi = mi\*Pi

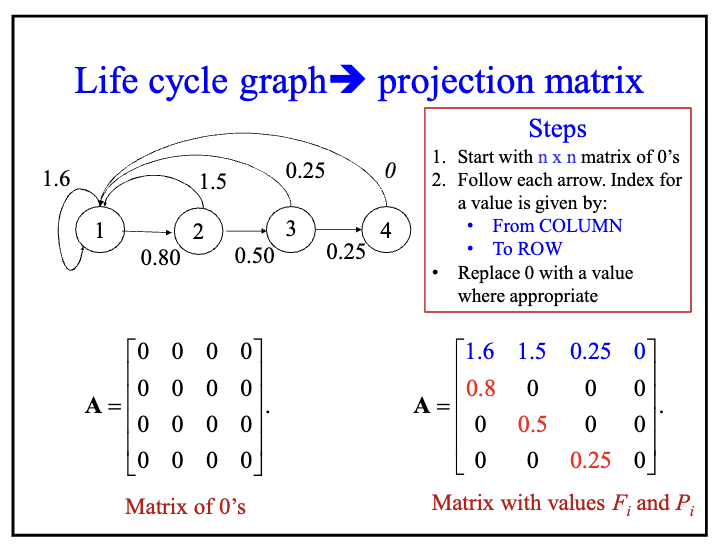
Know how to draw life cycle graphs for age- and stage-structured populations, and derive population projection matrices from the life cycle graphs! Also, know how to draw a life cycle graph from population projection matrices.

Stable age/stage distribution, reproductive values and λ; how are these calculated from the population projection matrices.

Lambda: largest eigenvalue of A

SAD: right eigenvector

Reproductive values: left eigenvector

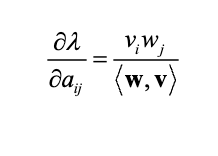
What are sensitivities and how are they calculated? Know the formula and the symbols.

Sensitivity: how would lambda change in response to small, absolute changes in a vital rate?

\

What do they tell you regarding the population dynamics? What do they quantify?

1. predict response to lambda to perturbations in vital rates
2. conservation and management
3. decompose observed changes in lambda
4. research
5. evolutionary studies

How do you interpret sensitivities and are they used in ecological and evolutionary studies?

The new matrix provides the sensitivity values which are a prediction of changes to whatever value used to be in that spot in the matrix

What are the problems associated with sensitivities?

1. deterministic, asymptotic analysis
2. deals with hypothetical situations
3. some demographic parameters may be less variable, resistant to change or may not change at all
4. management options can be limited to impact the most influential vital rates
5. interpret results with caution

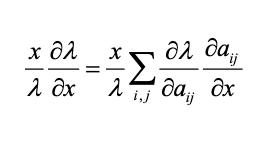
What are elasticities, what do they tell you? How are they calculated? How do they differ from sensitivities?

how would lambda change in response to small, proportional changes in a vital rate

elasticities are the lower-level sensitivities multiplied by x/lambda

Interpretation of sensitivities and elasticities: How can they be used in the management of an endangered species or a pest?

We can predict how to growth rate would respond to various conservation methods

Stage-structured matrix models: What are they? How do they differ from age-structured models?

Instead of being separated by age, they are separated by parts of their life

Differences: use stage structured when…


1. organisms with complex life-cycles
2. when something other than chronological age affects birth and death rates more strongly
3. when age is difficult to estimate

Parameters of stage-structured matrix models

1. regardless of the stage structure, underlying vital rates are essentially the same
2. from these, one can calculate matrix entries
3. parameter estimation:


1. similar to age-structured models
2. stage-specific survival

Given an age- or stage-structured projection matrix **A** and population vector at time *t* (**n**t), know how to project population size with age/stage structure to time *t* + 1. Know the population projection equation.

n(t+1)= An(t)

Interpretation of results of stage-structured matrix models

1. other analyses will also proceed as in the age-structured models


1. population growth rate
2. SAD
3. stage-specific reproductive values
2. sensitivity analysis

Why are matrix population models so popular? How can they be used in wildlife conservation and management?

They help us determine what age or stage class needs the most help and if they need help with their reproductive or survivorship rates

What are metapopulations? Why is the metapopulation concept relevant in wildlife conservation/management?

Metapopulation: a set of local populations that are connected by migration

Tells us about local extinction and recolonization of patches

How do simple models of metapopulation dynamics differ from standard models of single population dynamics?

metapopulation models have several patches separated by a given distance

Why are metapopulation extinction probabilities generally lower than single population extinction probabilities (assuming independence of local population dynamics)? Be able to show this using example calculations.

Because it can be recolonized by members of another patch

a single population will go extinct if lambda < 1

p(regional) = p(local)^x

Why are isolated populations more likely to go extinct than a network of connected populations?

they will not have recolonization

Levins model: What are the parameters/variables, and what is being modeled?

Parameters


1. considers a population of large number of homogeneous local populations
2. population dynamics within a patch are simplified to occupied or unoccupied
3. focuses on the balance between local extinction and recolonization
4. models the rate of change in metapopulation size, measured by the fraction of patches occupied

Levins model: Model assumptions

1. large number of homogeneous patches
2. constant pc and pe over time
3. asynchronous local population dynamics
4. size, quality, and spatial configuration of patches are not important
5. local population dynamics are not important
6. empty patches can be colonized by propagules from outside of the metapop system
7. an increase in F reduces metapopulation extinction rate through rescue effecr

Levins model: Equilibrium solution

1-(pe/pc)

Propagule rain and how it can influence metapopulation dynamics

* propagules: individuals that colonize an empty patch
* colonization of empty patches by propagules from elsewhere
* assume propagules are raining from outside the system
* empty patches can be colonized by propagules from elsewhere

The rescue effect and how it can influence metapopulation dynamics

rescue effect: the reduction in metapopulation extinction rate that occurs when more sites are occupied


1. dispersers from occupied sites will rescue smaller sites which may otherwise go extinct
2. thus, an increase in F will reduce metapop extinction risk, and increase equilibrium F

How patch size, patch quality, spatial structure, and connectivity/isolation can influence metapopulation colonization, extinction, and occupancy rates (i.e., the fraction of habitat patches occupied)

patch size decreases extinction

patch quality decreases extinction

connectivity increases colonization

Incidence Function Model (IFM)

1. allows patch size and quality to vary
2. does not assume infinite number of patches
3. explicitly considers size and spatial structure of patches
4. permits parameter estimation using real data

Source-sink dynamics including definitions of sources, sinks and pseudo-sinks

based on the balance between B and D and E and I

when B is density-dependent, a source population may look like a sink at high density → Pseudosink

Various types of “metapopulation structures”

Classic, Mainland- Island, Patchy Population, mixture, Source-Sink, and Relict metapop

What is PVA? Why use it?

an analysis that uses data in an analytical or simulation model to measure the risk of extinction or a closely related measure of population viability, such as the proportion of simulated populations that end above some size after some specified period of time

why use it

* ranking management options
* estimating harvest quote
* reserve design
* analyzing and synthesizing field data

Risk

probability of an adverse event

Risk assessment

the process of obtaining quantitative measures of risk levels

Absolute risk

risk faced by a population/species regardless of other populations/species

Relative risk

risk faced by a population/species relative to other populations/species

background risk

risk of extinction of a population under natural conditions

added risk

an increase in risk that results from unnatural forces

probability of extinction

probability that a population declines to 0

probability of quasi-extinction

probability that a population falls below some specified threshold

probability of persistence

1 - (prob of extinction)

time to extinction

an estimate of time for extinction to occur

monte carlo simulation

simulation of a probability model, or a random process

inbreeding/inbreeding depression

reduction in fitness due to inbreeding

outbreeding depression

loss of fitness due to outbreeding

genetic introgression

movement of genes from outside of a pop

genetic restoration or rescue

improvements in fitness of inbred pops from immigration of genetically divergent individuals

What are the main factors (deterministic, stochastic and management, etc.) to consider in PVA, and why?

1. Stochastic factors


1. environmental. catastrophes, demographic, genetic
2. deterministic


1. DD, allee effect
3. Genetic


1. inbreeding depression
4. management

Know the PVA components and steps

1. identification of objectives/questions
2. collation and analysis of data
3. selection of models
4. estimating model parameters
5. running the model
6. sensitivity analysis
7. evaluation of results and assumptions

criteria for evaluating PVAs

1. objectives/questions
2. model and model structure
3. data
4. analysis/implementation of the model
5. handling the unknown factors
6. presentation and interpretation of results
7. peer review

Why are some PVAs (or the PVA process itself) have been criticized?

1. single species focus
2. data needs
3. predictive accuracy issues
4. risk criteria
5. identification of the causes of decline
6. inappropriate use or abuse of PVA methodologies

Know various types of PVA models and their data requirements and limitations

1. SPOM


1. simplest data requirements
2. Count based


1. based on estimates of abundance over time
2. No DD, age- or stage- structured
3. structured


1. age or stage structured stochastic matrix models
4. Individual-based metapopulation models


1. amount of data required is often limiting factor
5. Integrated population models


1. utilize multiple data types (abundance, CMR)

Why is host-parasite interaction considered to be a (+, -) interaction?

Predation and Parasitism

Why do wildlife managers and conservation biologists need to worry about diseases? Why model disease dynamics?

1. wildlife are intermediate hosts or vectors for many human and livestock diseases
2. cause of decline or local extinction of many species
3. an important cause of amphibian population declines and biodiversity loss

Microparasites vs. macroparasites

Macroparasites: multi-cellular and long-lived

Microparasites: rapid reproduction, fast population increase within the host

vertical vs horizontal transmission

Vertical: transmission from parents to offspring

horizontal: direct or indirect contact

Box model

Open: Susceptible, Infectious, Recovered

Closed: Susceptible (Infection) → Infectious (Recovery or death) → Recovered

SIR differential equations