The structure of polymer molecules and the random walk model

Equation for random walk

R_{0 ² = Na²}

R_{0 ² =} mean square end to end distance.

N = no. steps taken in random walk/monomer size

a² = number of monomers per molecule

Conditions under which Random walk applies:

•    Negligible monomer volume.

•     No interactions between monomers.

•      Successive steps uncorrelated.

Solvent in which conditions apply

Theta solvent

Good solvent

• monomers repel one another/large volume

• polymer structure more swollen than random walk with longer end-to-end distance

Poor solvent

• Monomers attract each other hence stick together

• polymer structure less swollen than random walk

Theta solvent (θ)

• Monomers slightly attract each other

• significant volume

• hence 2 effects cancel each other out

Other examples of random walk

1. Diffusion

2. Statistical quantities

3. Financial markets

Flory Model

This is a model for a good solvent. We can guess this because the proportionality is R ~ N^3/5 and the exponent 3/5 is greater than the random walk value of ½, so the chain is more swollen. (Remember the random model walk is for a theta solvent [or in a melt].)

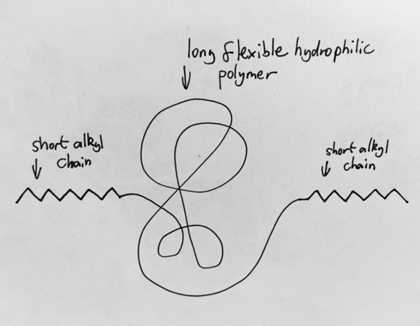
Is this polymer, if dissolved in water, likely to form a gel?

1. Yes

2. Short alkyl chain property:

   Non-polar molecule so doesn’t dissolve in water so will want to separate. By moving hydrophobic molecule closer to H20 reduces hydrophobic interactions.

   Alkyl chains form assemblies/i .e. cluster together -via cross-linking

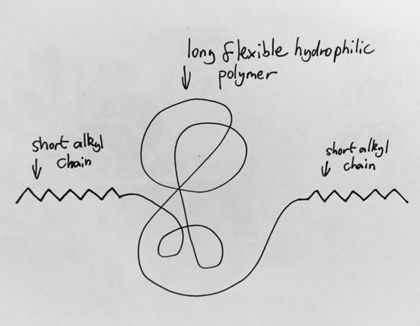
Essential requirement for formation of gel

cross-linking between molecules.

Helmholtz free energy of a system

max work that can be extracted from that system

Effect of decrease in entropy on extension and no . possible configurations

extension increases, and no. possible configurations decreases hence positive elastic restoring force i.e. material is elastic.

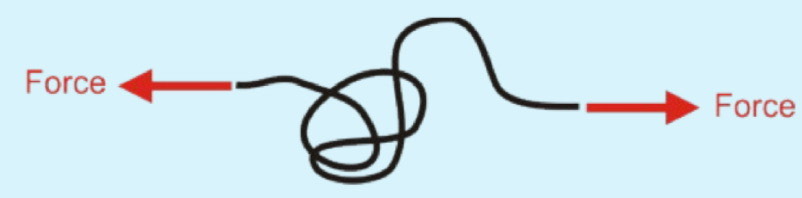
S-driven elasticity (Entropy driven elasticity)

• Ideal polymer

• Chains extend

• Chemical bonds don’t stretch

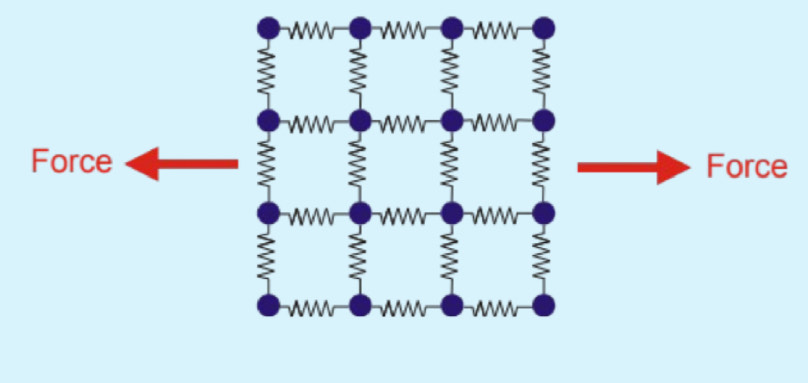
U-driven elasticity (Internal energy driven elasticity)

• e.g. metal

• Chemical bonds do stretch

2 different origins for elasticity:

1. In a crystalline material, capacity to do work stored by a higher potential energy within it.

2. Stretched rubber band no storage of potential energy- capacity to do work stored by lower configurational entropy within material.

How does elasticity arise in a crystalline material?

From change in internal energy(U) - caused by stretched bonds

How does elasticity arise in stretched rubber band?

• chemical bonds do not stretch

• BUT polymer chains within material unwind, when extended

• so lower entropy state

Elastic restoring force in ideal polymer chain (random walk model)

• thermal kinetic energy depends only on the temperature → doesn’t change

• internal energy U → doesn't change on extension

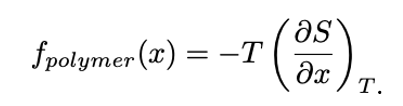
Elastic restoring force in Energy-elastic material (i.e. idealized metal, ceramic)

• at constant temperature, the entropy is independent of extension, x.

• BUT bonds between the atoms stretch, storing potential energy ⇒ changing U

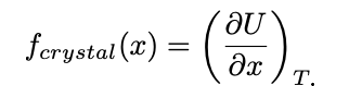
General equation for elastic restoring force:

A = Helmholtz free energy

U = Internal energy

S = Entropy

T = Temperature

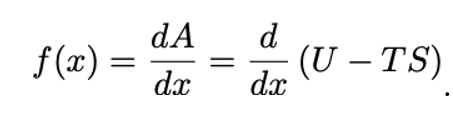
For a piece of metal in contact ,with its surroundings- reversible thermo = isothermal (temp doesn’t change)

Which can be broken up into its internal energy + entropy components.

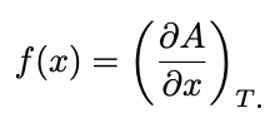
If a material is not thermally isolated

adiabatic so reversible not isothermal

What is the difference between a rubber and a gel?

• Rubber = formed from cross-linking polymer melt

• Gel = formed via cross-linking polymer solution

2 main macroscopic mechanical properties that characterize an elastomeric material?

1. Hyperelasticity

2. Very low stiffness (Young’s modulus)

What does configurational entropy generate?

A restoring force that contracts polymer size.

What occurs at thermal equilibrium ?

partial derivative of A (Helmholtz energy) with respect to R (T stays constant) = 0 i.e. A = maximized

Does the configurational entropy of polymer chain within sample of elastomeric polymeric materials increase/ decrease when stretched?

• Entropy decreases

• The uncoiling of the polymer chain upon stretching reduces no. potential config available so S decreases

Type of model for single polymer chain config

Random-walk-on-a-lattice

Type of model for gelation

Lattice percolation