Geometry Summative 5 Congruent Triangles - Sophomore Year

How are triangles classified?

by angles and sides

How do we name a triangle?

with the angle first and the sides second

CLASSIFYING BY ANGLE

CLASSIFYING BY ANGLE

Acute triangle

• 3 acute angles

• all angles measure less than 90 degrees

Equiangular triangle

• 3 congruent angles

• all angles have equal (the same) measure

Obtuse triangle

• 1 obtuse angle

• one angle measures more than 90 degrees

right triangle

• 1 right angle

• one angles measures 90 degrees

CLASSIFYING BY SIDES

CLASSIFYING BY SIDES

Equilateral triangle

• 3 congruent sides

• all sides have equal (the same) measure

Isosceles triangle

• 2 congruent sides

• at least 2 sides have equal (the same) measure

Scalene triangle

• 0 congruent sides

• no sides have equal (the same) measure

PROVING TRIANGLE INTERIOR ANGLES = 180

PROVING TRIANGLE INTERIOR ANGLES = 180

angles A, B, and C add up to…

so… <A + <B + <C =

180 degrees

= 180

FINDING MISSING INTERIOR ANGLES

FINDING MISSING INTERIOR ANGLES

how do we find a missing interior angle?

how do we find a missing interior angle?

we add up the other two interior angles and subtract the sum from 180 to get the missing angle

EXTERIOR ANGLES THEOREM

EXTERIOR ANGLES THEOREM

What is the exterior angle theorem?

The exterior angle of the triangle is equal to the sum of the two opposite interior angles of the triangle

FINDING MISSING EXTERIOR ANGLES

FINDING MISSING EXTERIOR ANGLES

How do we find a missing exterior angle?

we add up the two interior angles to find the missing angle

TYPES OF TRIANGLE CONGRUENCY THEOREMS

TYPES OF TRIANGLE CONGRUENCY THEOREMS

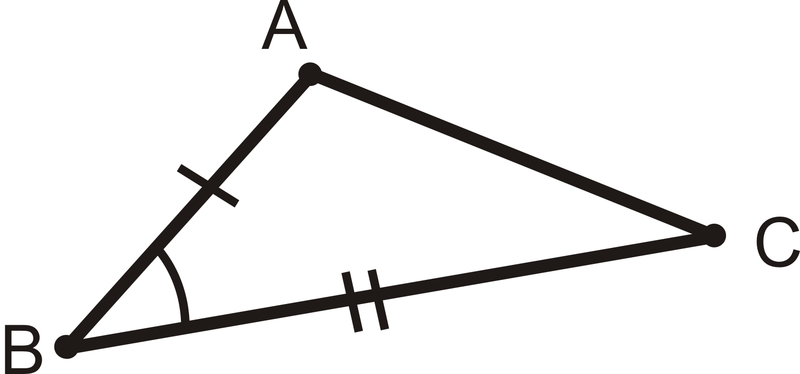
SAS - Side Angle Side

Two sides and the included angle are congruent

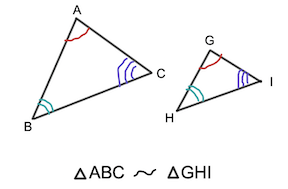
SSS - Side Side Side

All 3 sides are congruent

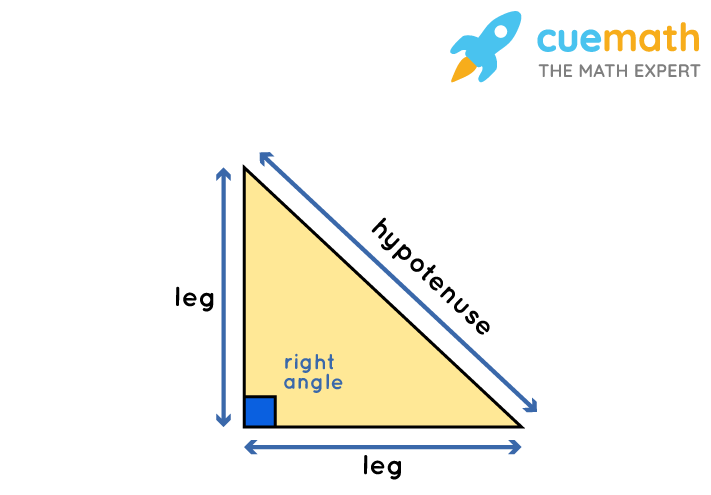
HL (right triangles only) Hypotenuse-Leg

The hypotenuse and one of the legs are congruent

ASA - Angle Side Angle

Two angles and the included side are congruent

AAS - Angle Angle Side

2 angles and a non-included side are congruent

SSA - Side Side Angle

does/doesn’t exist; not congruent/not provable

AAA - Angle Angle Angle

does/doesn’t exist; not congruent/not provable

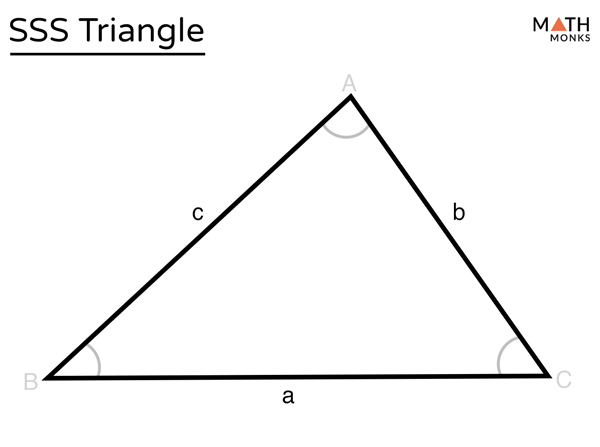
SSS Congruence

If 3 sides of a triangle are congruent, then the triangles are congruent

Proof Rules

always start with the given

the reasons can be either a definition, postulate, or theorem

do NOT assume anything if it is not in the given

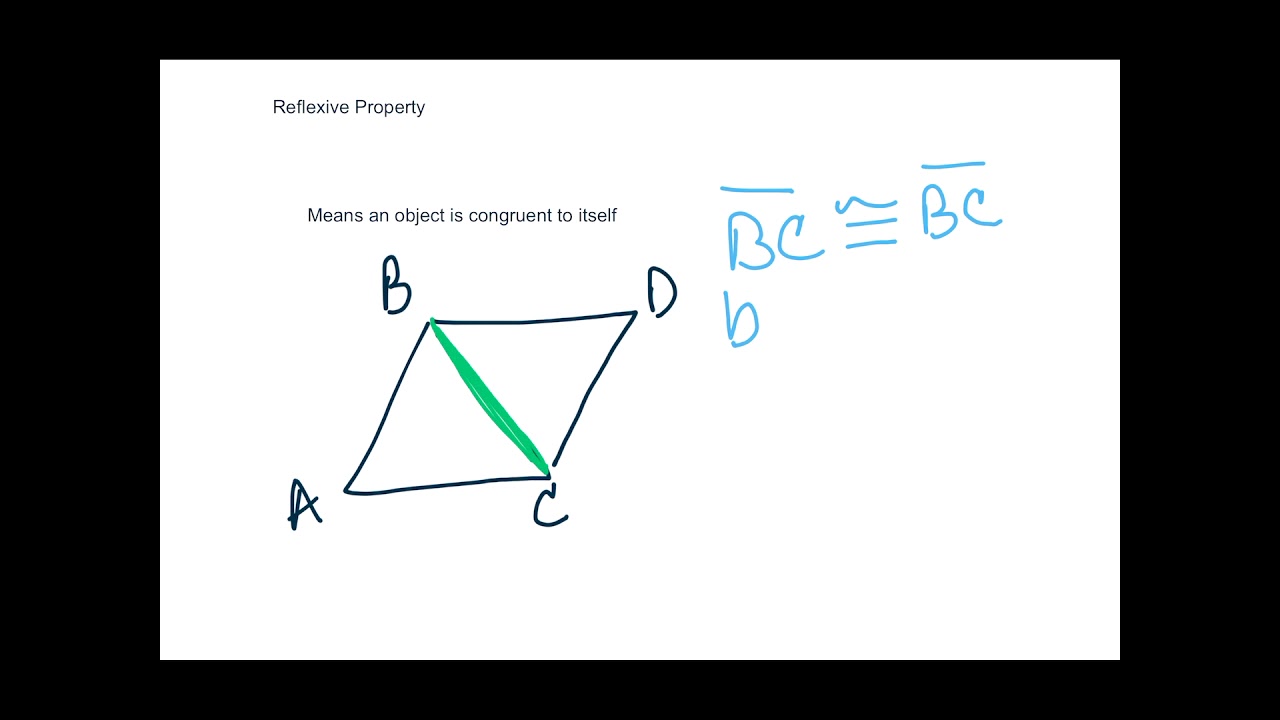
Reflexive Property

When the triangles have an angle or side in common

ex: AB = BA

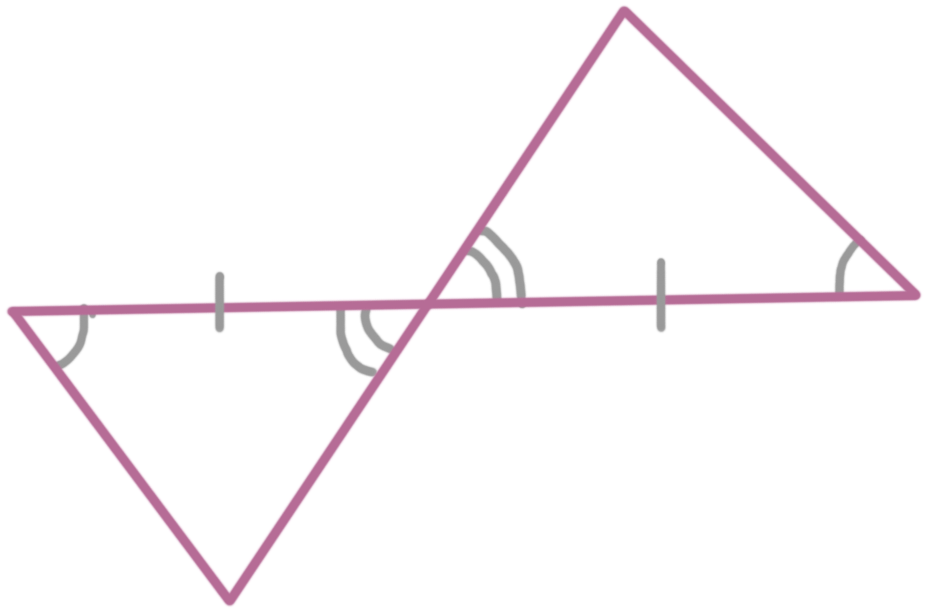
Vertical Angles are Congruent

When 2 lines are intersecting

Right Angles are Congruent

When you are given right triangles and/or a square/rectangle

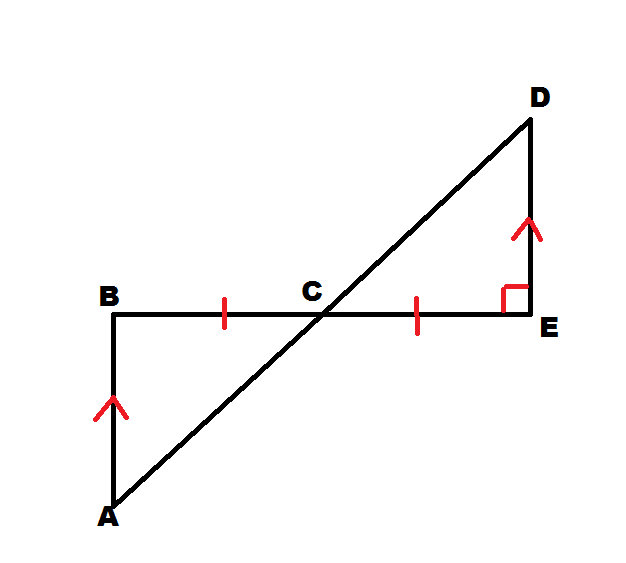
Alternate Interior Angles of Parallel Lines are Congruent

When the givens inform you that 2 lines are parallel

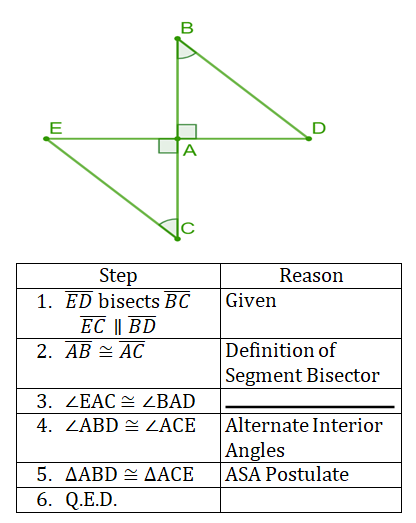
Definition of a Segment Bisector

Results in 2 segments being congruent

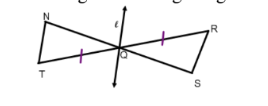
Definition of a Midpoint

Results in 2 segments being congruent

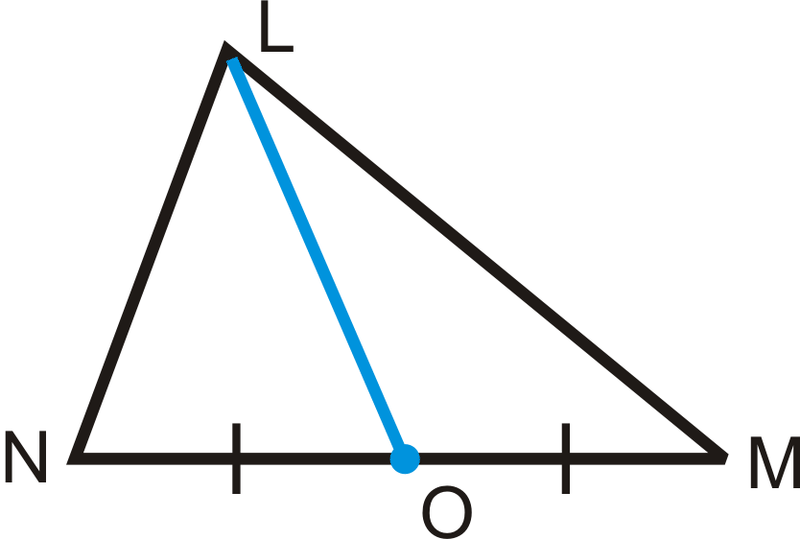
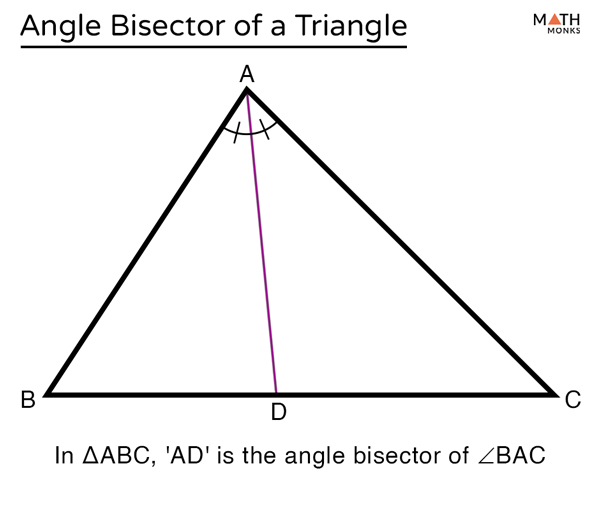
Definition of an Angle Bisector

Results in 2 angles being congruent

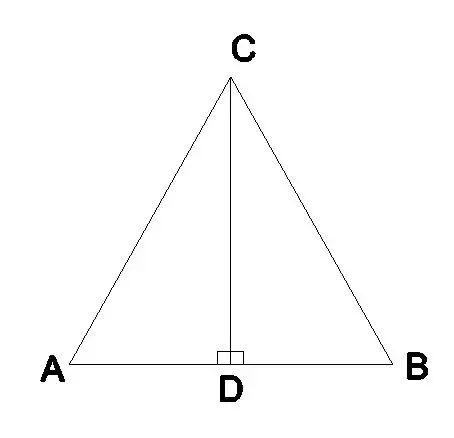
Definition of a Perpendicular Bisector

Results in 2 congruent segments and right angles

3rd Angle Theorem

If 2 angles of a triangle are = to 2 angles of another triangle, then the 3rd angles are =