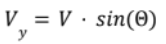Physics Key Equations

Key Equations for Physics first units

Relates final velocity (v) to initial velocity (v₀), acceleration (a), and time (t).

v = v₀ + at

Used for scenarios with uniform acceleration.

v = v₀ + at

Calculates displacement (Δx) under constant acceleration.

Δx = v₀t + ½at²

Links the squares of velocities to acceleration and displacement.

v² = v₀² + 2aΔx

Helpful when time is unknown or unnecessary. Highlights the connection between kinetic energy and work.

v² = v₀² + 2aΔx

Describes position (x) of an object moving at a constant velocity (v). Shows displacement as directly proportional to time for constant velocity.

x = x₀ + vt (for constant velocity)

Calculates average velocity (v_avg) for uniformly accelerating objects. Represents the arithmetic mean of initial and final velocities.

v_avg = (v + v₀) / 2

Defines average velocity as total displacement (Δx) divided by total time (Δt).

v_avg = Δx / Δt

Defines acceleration (a) as the rate of change in velocity (Δv) over time (Δt). Indicates how quickly an object accelerates or decelerates.

a = Δv / Δt

Calculates displacement (Δx) using average velocity (v_avg) and time (t). Works for both constant and variable velocities.

Δx = v_avg * t

Computes displacement (x) from the average of initial and final velocities over time.

x = ½(v + v₀)t

Δx = v_avg * t

Simplifies distance calculations over a time period.

Used to find an object’s position without acceleration.

x = x₀ + vt (for constant velocity)

Sine

Opposite/Adjacent

Cos

Adjacent/Hypotenuse

Tan

Opposite/Adjacent

Scalar Magnitude (R)

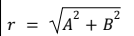
Resultant Vector Direction

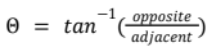
Horizontal Vector Complex

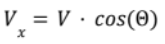
Vertical Vector Complex